Calculus Math 133 - Lecture 2.2

Dr Makram Math

29 Mar 202332:33

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture introduces the concept of limits in calculus, focusing on understanding how to calculate limits using a calculator and graphical analysis. The speaker begins with a practical example, demonstrating how to find the limit of a quadratic function as x approaches a specific value. The lecture then delves into the rigorous definition of limits, explaining the notation and the process of approaching a value from both the right and left sides. The importance of one-sided limits is emphasized, with examples illustrating how they can differ and how their equality is crucial for the existence of a limit at a point. The speaker also explores the concept of infinite limits and vertical asymptotes, providing clear definitions and graphical examples. The lecture concludes with a 'try and check' exercise, reinforcing the understanding of limits through practical application.

Takeaways

📚 The concept of limits in calculus involves understanding how a function behaves as its input approaches a certain value, which can be demonstrated through calculations and graphical analysis.
🔢 To estimate the limit of a function as x approaches a certain value, one can use a calculator to input values of x that are progressively closer to that value and observe the trend in the function's output.
📈 The graphical representation of a function can help visualize the limit by observing the behavior of the graph as x approaches the value from the left and right.
🏁 The limit of a function at a point exists if the left and right limits agree and are equal to the function's value at that point, or if the function is not defined at the point but the left and right limits exist and are equal.
📉 For functions that are not defined at a certain point, the limit can still exist if the left and right limits are equal, even if they are different from the function's value at that point.
➡️ One-sided limits, also known as left-hand and right-hand limits, are used to describe the behavior of a function as it approaches a point from either the left (less than the point) or the right (greater than the point).
🚫 A limit does not exist at a point if the left and right limits are not equal, indicating the function behaves differently on either side of the point.
🔁 The value of the function at a point (often denoted as f(a)) is not necessarily the same as the limit of the function as x approaches a, emphasizing the distinction between the function's value and its limit.
🌌 Infinite limits occur when the function's output becomes arbitrarily large (positive or negative infinity) as the input approaches a certain value, which can be determined by analyzing the function's behavior as x approaches that value.
📉 A vertical asymptote is a vertical line on the graph of a function where the function approaches infinity or negative infinity as x approaches a certain value, indicating a point or values where the function is not defined.
📚 The existence of a limit, its value, and the identification of vertical asymptotes are fundamental to understanding the behavior of functions in calculus, which is crucial for further mathematical analysis and applications.

Q & A

How is the limit of a function obtained using a calculator?
-The limit of a function is obtained using a calculator by inputting values of the variable (x) that are increasingly close to the point of interest but not equal to it. This is done for both sides of the point (from the left and from the right) to observe how the function values approach as x approaches the given point.
What is the function used as an example to demonstrate limits in the script?
-The function used as an example is f(x) = x^2 - x + 2, and the limit is sought as x approaches 2.
How does the value of a function at a point relate to the limit at that point?
-The value of the function at a point (f(a)) may or may not be equal to the limit of the function as x approaches a. The limit is the value that the function approaches as x gets arbitrarily close to a, and it can exist even if the function is not defined at the point a.
What is a one-sided limit and how is it different from a regular limit?
-A one-sided limit is the limit of a function as the variable approaches a certain point from either the left (denoted as a-) or the right (denoted as a+). It is different from a regular limit in that it only considers the behavior of the function from one direction, whereas a regular limit considers the function's behavior as it approaches the point from both directions.
What does it mean for a limit to not exist at a certain point?
-A limit is said to not exist at a certain point if the one-sided limits from the left and right do not match; that is, the values that the function approaches from either side are different, indicating that the function does not settle to a unique value as it gets closer to that point.
How is the limit of a function related to its graph?
-The limit of a function can often be inferred from its graph. If the graph of the function approaches a certain y-value as x gets closer to a particular x-value, then the limit at that point is the y-value the graph approaches. If the graph does not settle to a single y-value from both sides, then the limit does not exist at that point.
What is a vertical asymptote and how does it relate to limits?
-A vertical asymptote is a vertical line on the graph of a function where the function's values increase without bound (go to infinity or negative infinity) as the input (x) approaches a certain value. It relates to limits in that the function does not have a value at the asymptote, but the one-sided limits as x approaches the value from either side can be infinite.
What is the rigorous definition of a limit?
-The rigorous definition of a limit states that the limit of a function f(x) as x approaches a is equal to L (denoted as lim(x→a) f(x) = L) if for every number ε > 0, there exists a number δ > 0 such that whenever 0 < |x - a| < δ, it follows that |f(x) - L| < ε.
What are the conditions for a function to have a limit as x approaches a certain point?
-A function has a limit as x approaches a certain point if the left and right limits exist and are equal. If the left and right limits are not equal, the limit does not exist at that point, even if the function is defined at the point.
How does the behavior of a function as x approaches infinity or negative infinity relate to infinite limits?
-If a function's value grows without bound (becomes infinitely large) as x approaches infinity or negative infinity, we say that the function has an infinite limit at that point. This is denoted as lim(x→∞) f(x) = ∞ or lim(x→-∞) f(x) = ∞ for positive infinity, and similarly with a negative sign for negative infinity.
What is the significance of finding the left and right limits separately when determining the limit of a function at a point?
-Finding the left and right limits separately is significant because it allows us to determine whether the function approaches the same value from both sides of a point. If the left and right limits are not equal, it indicates that the function does not have a well-defined limit at that point, even if the function is defined at the point itself.

Outlines

00:00

📚 Introduction to Limits through Calculations

The first paragraph introduces the concept of limits within the context of a mathematical lecture. It explains how to calculate limits using a calculator with the function f(x) = x^2 - x + 2 as an example. The process involves substituting values of x close to 2 from both sides to observe the behavior of the function as x approaches 2. The conclusion is that the limit of the function as x approaches 2 is 4. The paragraph also includes a graph representation to visualize the limit and concludes with the formal definition of a limit, emphasizing the difference between the value of the function at a point and the limit as x approaches that point.

05:03

📈 Understanding Limit Behaviors through Graphs

The second paragraph delves into the graphical representation of limits, illustrating different scenarios where the function is defined at a point 'a' and how the limit can be equal to L, different from L, or not existent based on the behavior of the function from the right and left. It also discusses the concept of one-sided limits and provides an example of the limit of (x - 1) / (x^2 - 1) as x approaches 1, concluding that the limit is 0.5. The importance of understanding that the limit can differ from the function's value at a point is emphasized, and the definition of one-sided limits is introduced.

10:06

🚦 Defining One-Sided Limits and Their Significance

The third paragraph focuses on the definition of one-sided limits, using the example of a heavy side function h(t) which is defined differently for negative and non-negative values of t. The concept of right (0+) and left (0-) limits is introduced, and it's explained that the existence of one-sided limits does not necessarily imply the existence of a limit at the point. The paragraph also includes a definition of the left-hand and right-hand limits and how to determine them graphically. The importance of both one-sided limits being equal for the existence of a limit at a point is highlighted.

15:08

🔍 Analyzing Limits and One-Sided Limits in Examples

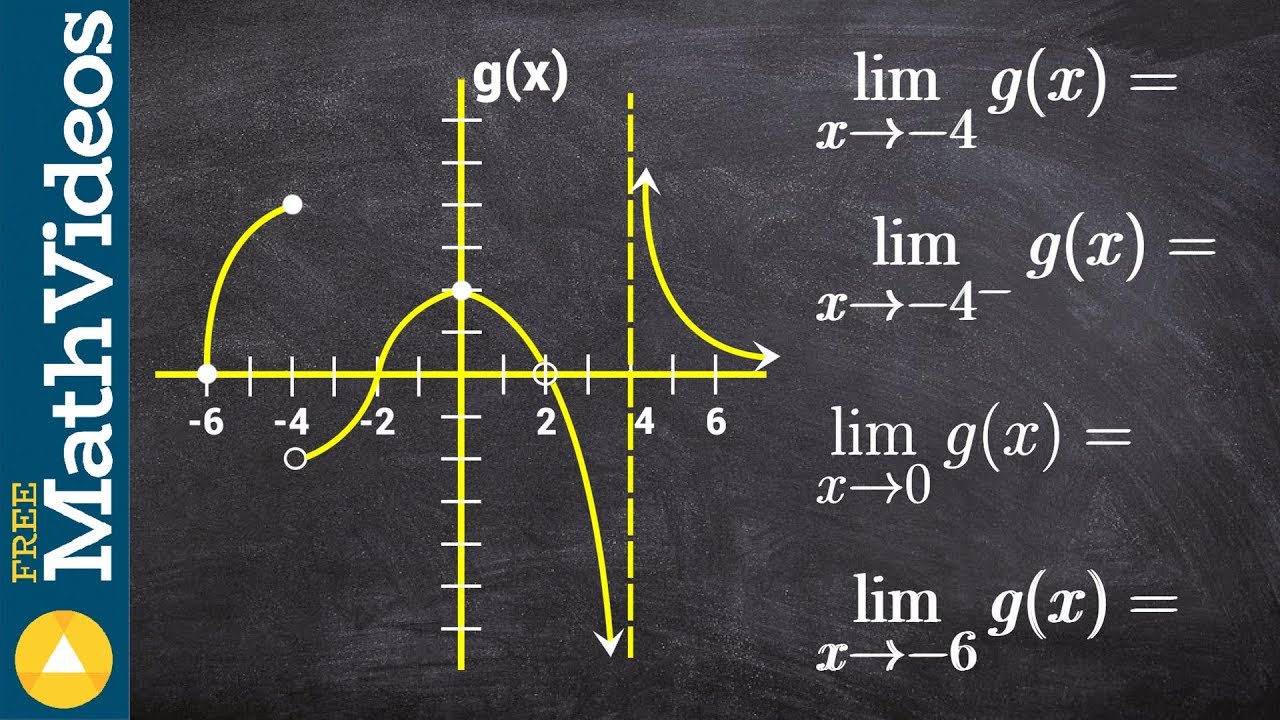
The fourth paragraph provides an example to find limits and one-sided limits for given functions. It discusses how to approach a point from the left and right to determine the limit as x approaches a specific value. The paragraph covers various scenarios where the limit exists or does not exist based on the values obtained from approaching the point from both sides. It also touches on the concept of infinite limits and how they can be determined.

20:09

∞ Exploring Infinite Limits and Vertical Asymptotes

The fifth paragraph explores infinite limits, explaining what it means for a function to tend towards positive or negative infinity as x approaches a certain value. It uses the tangent function as an example to illustrate this concept. The paragraph also introduces the concept of vertical asymptotes, explaining that they occur when the limit as x approaches a certain value is either positive or negative infinity. It further explains how to identify vertical asymptotes from the graph of a function and provides an example using the tangent function.

25:11

📉 Identifying Vertical Asymptotes from Function Graphs

The sixth paragraph continues the discussion on vertical asymptotes, specifically focusing on how to identify them from the graph of a function. It uses the tangent function as an example, noting that vertical asymptotes occur at points where the cosine of x is zero. The paragraph explains the periodicity of the cosine function and how to determine the points that correspond to vertical asymptotes. It concludes by emphasizing the importance of checking both left and right limits to confirm a vertical asymptote.

30:13

🏁 Concluding with Vertical Asymptotes and Limit Calculations

The seventh and final paragraph wraps up the lecture by confirming vertical asymptotes from the graph of a function. It discusses how to determine the limit as x approaches specific values and how these limits can be used to identify vertical asymptotes. The paragraph provides examples and concludes with the identification of vertical asymptotes at x = 3, x = 7, and x = -4, based on the behavior of the function's graph. It reiterates the concept that a limit does not always exist even if the function is defined at a point, and that vertical asymptotes can be identified from the direction in which the function's graph approaches a certain value.

Mindmap

Keywords

💡Limits

Limits are a fundamental concept in calculus that describe the behavior of a function as its input approaches a particular value. In the video, the lecturer introduces limits through computations and graphical analysis, using functions like f(x) = x^2 - x + 2 to demonstrate how to find limits as x approaches a certain value. Limits are crucial for understanding continuity, differentiability, and the overall behavior of functions in calculus.

💡Calculator

A calculator is an electronic device used for performing arithmetic operations and computations. In the context of the video, the lecturer mentions using a calculator to approximate limits by substituting values of x close to the point of interest. For instance, to find the limit as x approaches 2, values like 1.9, 1.99, and 1.999 are used to observe the trend and make an educated guess about the limit.

💡Function

A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. The video discusses functions such as f(x) and g(x), using them to illustrate the process of finding limits. Functions are central to the study of limits as they provide the expressions that are evaluated at different points to understand their behavior.

💡Graph

A graph is a visual representation of data, showing the relationship between variables. In the video, the lecturer uses graphs to help visualize and understand limits. By plotting points and observing the function's behavior as x approaches a certain value, the graph provides a geometric interpretation of the limit concept. For example, the lecturer discusses how the graph of f(x) approaches the value of 4 as x gets closer to 2.

💡One-Sided Limits

One-sided limits, also known as directional limits, are limits that approach a point from either the left or the right. The video explains the concept of one-sided limits by considering the behavior of functions as x approaches a value from both directions. This is important in understanding discontinuities and the behavior of functions at endpoints of intervals.

💡Vertical Asymptote

A vertical asymptote is a vertical line that a graph approaches but never actually intersects. In the video, the lecturer discusses vertical asymptotes in relation to functions that tend towards infinity or negative infinity as x approaches a certain value. The concept is illustrated with examples like tan(x), where the讲师 (lecturer) explains that values of x for which the cosine is zero create vertical asymptotes.

💡Infinity

Infinity, in mathematics, is often treated as an unbounded quantity that is greater than any number. The video explores the concept of limits approaching infinity, which occurs when the function's value grows without bound as the input (x) approaches a certain point. This is exemplified by functions that have vertical asymptotes or when the denominator of a fraction approaches zero.

💡Conjecture

A conjecture is an opinion or conclusion formed based on incomplete information, which is often the result of observation or experimentation. In the context of the video, the lecturer makes conjectures about the value of limits based on the observed behavior of the function as x approaches certain values. For example, by substituting values close to 2 into the function f(x), the lecturer conjectures that the limit as x approaches 2 is 4.

💡Continuity

Continuity in calculus refers to a property of functions where there are no breaks, jumps, or asymptotes in the graph of the function. The video touches on continuity in the context of limits, explaining that for a function to be continuous at a point, the limit as x approaches that point must equal the function's value at that point. The lecturer contrasts this with cases where the function has a removable discontinuity or an undefined value at a point.

💡Rigorous Definition

A rigorous definition is a precise and comprehensive explanation of a concept, often used in mathematics to eliminate ambiguity. The video includes a rigorous definition of a limit, stating that the limit of f(x) as x approaches a is equal to L if the values of f(x) can be made arbitrarily close to L by choosing x values sufficiently close to a, but not equal to a. This formalizes the intuitive idea of a limit used throughout the lecture.

💡Tangent Function

The tangent function, often abbreviated as tan(x), is a trigonometric function that measures the ratio of the length of the side opposite to an angle in a right triangle to the length of the adjacent side. In the video, the lecturer uses the tangent function to illustrate the concept of infinite limits and vertical asymptotes, noting that tan(x) approaches infinity or negative infinity at certain angles, such as x approaching pi/2.

Highlights

Introduction to limits using calculations with the example of the function f(x) = x^2 - x + 2.

Explains how to obtain limits using a calculator by taking values close to the point of interest.

Demonstrates the concept of limits by showing how values approach a certain number without actually reaching it.

Discusses the rigorous definition of the limit and its notation.

Differentiates between the value of the function at a point and the limit at that point.

Introduces the concept of one-sided limits (left and right) and their definitions.

Illustrates the difference between the function value and the limit with the example of x - 1 / (x^2 - 1) as x approaches 1.

Explains the existence of one-sided limits and when the overall limit does not exist due to the discrepancy between left and right limits.

Provides the definition of a limit involving the equality of left and right one-sided limits.

Discusses the concept of vertical asymptotes and their relation to infinite limits.

Uses the tangent function as an example to explain vertical asymptotes and their values at specific points.

Explains how to identify vertical asymptotes from the graph of a function.

Provides examples to find limits and vertical asymptotes for different functions and values.

Discusses the difference between the value of a function at a point and the limit at that point, emphasizing that they are not always the same.

Explains the concept of infinite limits and how they can be either positive or negative infinity.

Details the conditions under which a vertical line x = a is considered a vertical asymptote for a function.

Concludes the lecture with a summary of key points and a reminder of the importance of understanding limits and their applications.

Transcripts

Browse More Related Video

Limits via Graphs!

Evaluate all the limits from a given graph

Limits! Part 1

Calculus AB/BC – 1.3 Estimating Limit Values from Graphs

Math 11 - Sections 1.1-1.2

Limits of piecewise functions | Limits and continuity | AP Calculus AB | Khan Academy

Related Tags

Calculus Limits Infinite Limits One-Sided Limits Vertical Asymptote Graph Analysis Mathematical Concepts Function Behavior Tangent Function Educational Content Math Tutorial