Calculus Chapter 5 Lecture 46 Differences II
TLDRIn this calculus lecture, Professor Greist introduces the concept of discrete calculus, focusing on finite differences for sequences. He explains forward and backward differences, drawing parallels to derivatives, and demonstrates with examples like the Fibonacci sequence and exponential functions. The lecture delves into the discrete version of e, exploring the properties of falling powers and their relationship to polynomial sequences. It concludes with an introduction to operators in discrete calculus, highlighting the algebraic manipulation of these operators for differencing and anti-differentiation, offering a novel perspective on the subject.
Takeaways
- 📚 The lecture introduces the concept of discrete calculus, focusing on the construction of a derivative for sequences, which is simpler than for smooth functions but still profound.
- 🔍 The forward difference of a sequence a_n is defined as Δ a_n = a_{n+1} - a_n, which is analogous to the derivative but with a unit difference in the input.
- 🔙 The backward difference is defined as ∇ a_n = a_n - a_{n-1}, providing a different perspective on the sequence's change by looking at the past term.
- 📈 Examples given include sequences like the constant sequence, the Fibonacci sequence, and 2^N, each demonstrating unique behaviors under forward differences.
- 🔢 The script explains that polynomial sequences have a characteristic pattern when differences are taken repeatedly, eventually leading to a constant zero sequence.
- 📉 The concept of falling powers n ↓ k is introduced as a discrete calculus version of monomials, which simplifies the process of taking differences.
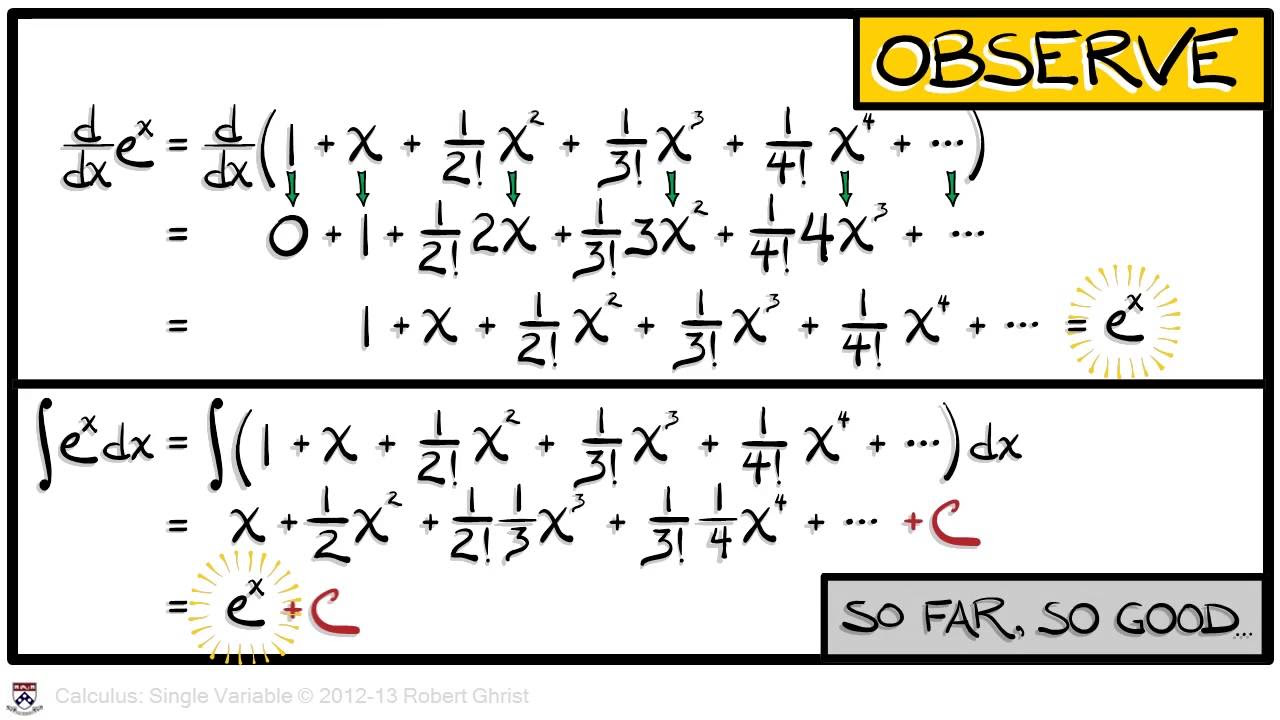
- 🌟 The discrete version of e (Euler's number) is shown to be 2, and the sequence 2^N is highlighted as having properties similar to the continuous e^x.
- 🔄 The lecture discusses operators in discrete calculus, such as the identity, left shift, and right shift operators, which can be manipulated algebraically.
- 🔧 The forward and backward differences are expressed in terms of these operators, providing a formulaic approach to understanding and calculating differences.
- 🔄 The inverse of the forward difference operator is explored, hinting at a method for 'anti-differencing' or reconstructing sequences from their differences.
- 🚀 The script concludes by emphasizing the importance of understanding and careful application of these concepts in the study of discrete calculus.
Q & A
What is the main focus of Professor Greist's lecture 46 on calculus?
-The main focus of the lecture is the construction of a discrete calculus, specifically building the notion of a derivative for a sequence.
What is the definition of the forward difference of a sequence?
-The forward difference of a sequence at position n, denoted as Δa at n, is defined as a(n+1) - a(n), which is the difference between the next term and the current term in the sequence.
How does the definition of a forward difference relate to the definition of a derivative?
-The forward difference is similar to the derivative in that it takes a difference in the output (a(n+1) - a(n)) and relates it to a difference in the input, but in the case of sequences, this difference is always 1.
What is the definition of the backward difference of a sequence?
-The backward difference, denoted as nabla a at N, is defined as a(n) - a(n-1), which is the difference between the current term and the previous term in the sequence.
What happens when you compute the forward difference of the Fibonacci sequence?
-When you compute the forward difference of the Fibonacci sequence, you obtain the Fibonacci sequence itself but shifted over by one step with an additional one out in front.
What does the forward difference of the sequence 2^N reveal about the sequence?
-The forward difference of the sequence 2^N is again 2^N, which is similar to how the exponential function e^x is its own derivative in continuous calculus.
What is the definition of a polynomial sequence in the context of discrete calculus?
-A sequence a is considered a polynomial of degree P if the (P+1)th forward difference is the constant zero sequence.
What are falling powers in discrete calculus, and how are they defined?
-Falling powers are discrete calculus versions of monomials. They are defined as n to the falling K, which is the product of n, n-1, ..., n-k+1, and for k equals 0, n to the falling 0 is defined as 1.
How does the forward difference of n to the falling K relate to the sequence itself?
-The forward difference of n to the falling K is K times n to the falling K-1, showing a direct proportionality between the difference and the sequence.
What is the discrete version of the constant e in calculus, and how does it relate to the sequence 2^N?
-In discrete calculus, the constant e is represented by the value 2 when evaluated at N equals 1. The sequence 2^N is the discrete version of e^x, as the forward difference of 2^N is the sequence itself, similar to e^x being its own derivative.
What is the significance of the operators in discrete calculus, and how do they help in understanding differences?
-Operators in discrete calculus transform sequences into other sequences. They help in understanding differences by allowing algebraic manipulation, such as expressing the forward and backward differences in terms of the left and right shift operators, and simplifying the computation of higher differences.
How can the concept of anti-differentiation or anti-difference be applied in discrete calculus?
-Anti-difference in discrete calculus can be thought of as reversing the differencing process. It involves summing all terms of a sequence that follow from a certain point and can be represented using a geometric series approach, but with caution regarding the sequence's properties.
Outlines
📚 Introduction to Discrete Calculus and Differences
Professor Greist introduces the concept of discrete calculus, focusing on the construction of derivatives for sequences. He explains the simplicity of this definition compared to derivatives of smooth functions and its profound implications. The lecture delves into the notion of finite differences, defining the forward and backward differences for a sequence and drawing parallels to the derivative concept. Examples are provided, such as the constant sequence, the Fibonacci sequence, and the sequence of powers of 2, to illustrate the behavior of differences in various scenarios.
🔍 Exploring the Properties of Differences and Falling Powers
This section explores the properties of differences and introduces the concept of falling powers as discrete calculus versions of monomials. The forward difference of n to the falling K is explained, and its utility is demonstrated through the example of squaring a sequence. The peculiarities of the difference of N squared are addressed, and the discrete version of the mathematical constant e is discussed, revealing its value as 2 in the context of discrete calculus. The summary also touches on the behavior of the sequence 2 to the N and its relation to the exponential function in continuous calculus.
🔄 The Algebra of Operators in Discrete Calculus
Operators in discrete calculus are introduced as tools that transform sequences. The identity operator, left and right shift operators, and the forward and backward difference operators are defined and their algebraic properties are discussed. The lecture explains how these operators can be manipulated algebraically to simplify the computation of higher differences. An example of calculating the second forward difference is given, and a general formula for the k-th forward difference is derived, highlighting the utility of operator algebra in simplifying complex calculations.
🔄 Discrete Indefinite Integrals and Anti-Differencing
The concept of indefinite integrals in discrete calculus is introduced, exploring the inverse of the forward difference operator. The geometric series approach is suggested for anti-differencing, and its validity is tested with a simple sequence example. The process of summing terms from a sequence to compute the inverse difference is described, and a cautionary note is given regarding the need for sequences to terminate in zeros or be summable for the method to work effectively. The summary concludes with a teaser for the next lesson, which will further explore discrete calculus in a digital context.
Mindmap
Keywords
💡Discrete Calculus
💡Forward Difference
💡Backward Difference
💡Sequence
💡Finite Differences
💡Polynomial Sequences
💡Falling Powers
💡Operators
💡Exponential Sequence
💡Indefinite Integral
Highlights
Introduction to the concept of a derivative for a sequence in discrete calculus.
The definition of the forward difference and its analogy to the derivative of a function.
Illustration of the backward difference and its relation to the slope of a sequence.
Examples of computing forward differences for linear and Fibonacci sequences.
The observation that the forward difference of an exponential sequence results in the same sequence.
Discussion on the parallels between differences and derivatives in the context of polynomial sequences.
Introduction of falling powers as discrete calculus versions of monomials.
Explanation of how the forward difference of n squared relates to falling powers.
The discrete version of e and its evaluation at N equals 1 resulting in the value 2.
The connection between the forward difference of 2 to the N and the behavior of e to the X.
Introduction to the concept of operators in discrete calculus and their algebraic manipulation.
The algebraic representation of forward and backward differences using operators.
Application of operator algebra to compute higher-order differences efficiently.
The concept of anti-differentiation or inverse differencing in discrete calculus.
A practical example demonstrating the inverse differencing process on a given sequence.
The cautionary note on the limitations and conditions for applying inverse differencing.
A preview of the next lesson's focus on fully digital applications of differencing and anti-differentiation in discrete calculus.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: