Calculus Chapter 5 Lecture 45 Sequences II

Penn Online Learning

23 Jun 201614:37

EducationalLearning

32 Likes 10 Comments

TLDRIn this calculus lecture, Professor Greist introduces the concept of sequences as discrete functions with natural number inputs and real outputs. He discusses the importance of sequences in digital contexts like music and imagery and highlights their unique behaviors, such as non-repeatability and aliasing. The lecture delves into the limits of sequences, using continuous methods to solve discrete problems, and explores examples including the golden ratio and the Fibonacci sequence, emphasizing the relevance of discrete calculus in understanding digital phenomena.

Takeaways

📚 We are transitioning to the last chapter of the course, focusing on sequences and discrete calculus.
🔢 Sequences are functions with discrete inputs and continuous outputs, which differ from the analog functions previously discussed.
🖥️ Discrete or digital inputs are common in music, imagery, and information, unlike the continuous inputs of analog functions.
🧮 We will revisit sequences with a focus on discrete calculus, redoing previous calculus work for functions with discrete inputs.
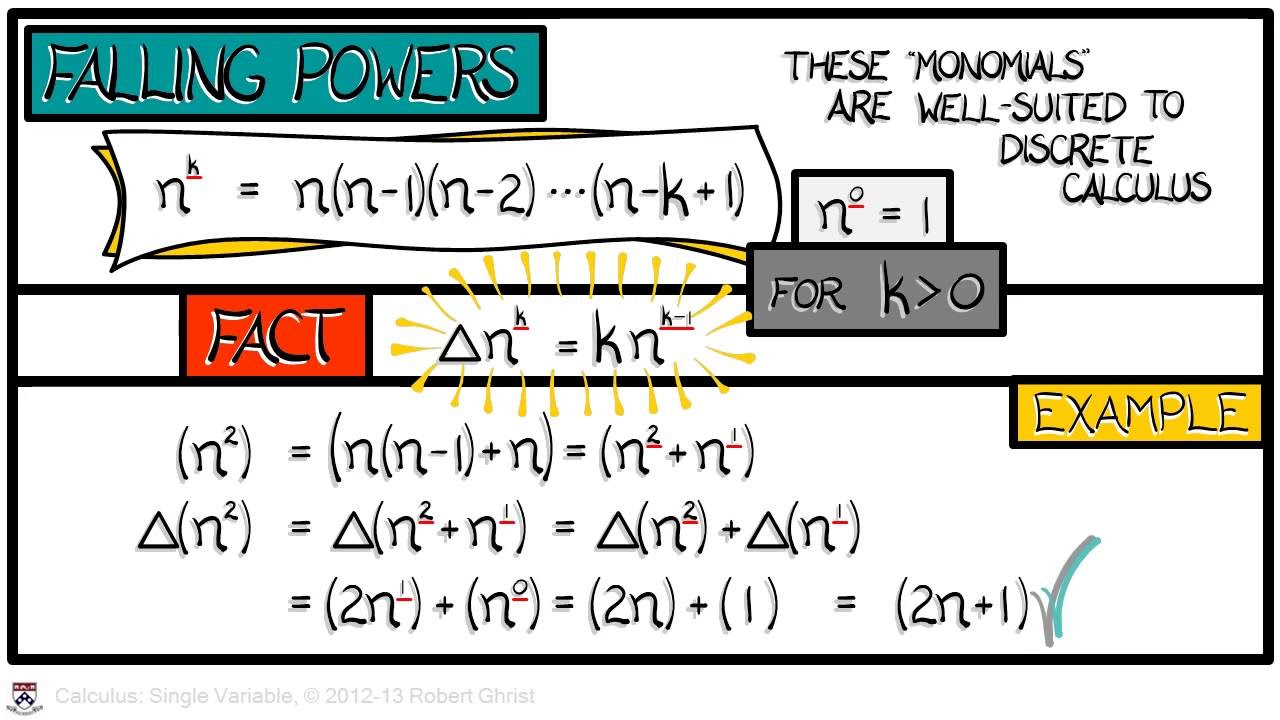
🔍 Notation for sequences will involve writing out terms like a₀, a₁, a₂, etc., focusing on the input-output relationship.
📈 Examples of sequences include polynomial-like (n²), exponential (2ⁿ), and alternating sequences (1, -1, 1, -1).
🌊 Non-repeating sequences like cos(n) exhibit wave-like behavior and are akin to visual phenomena like aliasing.
➖ Taking limits in discrete calculus primarily focuses on limits as n approaches infinity, similar to continuous calculus.
📏 Methods from continuous calculus, such as Taylor series, can be used to solve discrete problems.
🔗 Recursion relations are key in computing limits of complex sequences, such as nested square roots and continued fractions.
🧩 The golden ratio (φ) emerges from solving recurrence relations and is connected to the Fibonacci sequence.
🔍 Future lessons will explore the discrete analog of the exponential function and its relationship to derivatives.

Q & A

What is the main focus of the last chapter of the calculus course as described in the script?
-The main focus of the last chapter is on sequences, which are considered as discrete or digital input functions with an analogue output, and building a discrete calculus by reinventing concepts for these functions.
How are sequences defined in the context of the script?
-In the script, a sequence is defined as a function with discrete or digital input (natural numbers) and an analogue output (reals).
What is the difference between analog and digital functions as mentioned in the script?
-Analog functions have inputs and outputs that vary continuously, allowing for concepts like limits and differentials in calculus. Digital functions, such as sequences, have discrete inputs and are not amenable to smooth calculus.
What is an example of a sequence described in the script that behaves like a trigonometric function but does not repeat?
-The sequence described is 'cosine n', which exhibits wave-like behavior but does not repeat, unlike typical trigonometric functions.
What phenomenon is the script referring to when discussing an object that spins so fast it appears to spin at a different rate or direction?
-The script refers to the phenomenon of 'aliasing', which occurs when an object spins so fast that the visual refresh rate can't keep up, causing it to appear as if it's spinning at a different rate or direction.
What is the significance of taking limits in the context of sequences?
-Taking limits in the context of sequences is significant for understanding the behavior of the sequence as it approaches infinity, which is a key concept in discrete calculus and can be used in approximations like Taylor series.
How does the script suggest using continuous methods to solve discrete problems?
-The script suggests using continuous methods by applying the same principles used in continuous calculus, such as taking logarithms, using Taylor series, and applying Big O notation, to solve problems in discrete calculus.
What is the golden ratio and how is it related to the script's discussion on limits?
-The golden ratio, denoted by the symbol φ (phi), is a positive solution to the equation L^2 - L - 1 = 0, and it is approximately equal to 1 + √5 / 2. In the script, it is derived as the limit of a specific sequence and is a point of interest in the context of discrete calculus.
How does the script describe the process of finding the limit of a sequence that involves a recursion relation?
-The script describes the process by first denoting the limit by L, applying the limit to the recursion relation, substituting L for the terms, and then solving the resulting equation to find the limit.
What is the Fibonacci sequence and how does the script suggest it might relate to discrete calculus?
-The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. The script suggests that there is interesting mathematics behind the Fibonacci sequence and hints that calculus might provide insights into its properties.

Outlines

00:00

📚 Introduction to Discrete Calculus

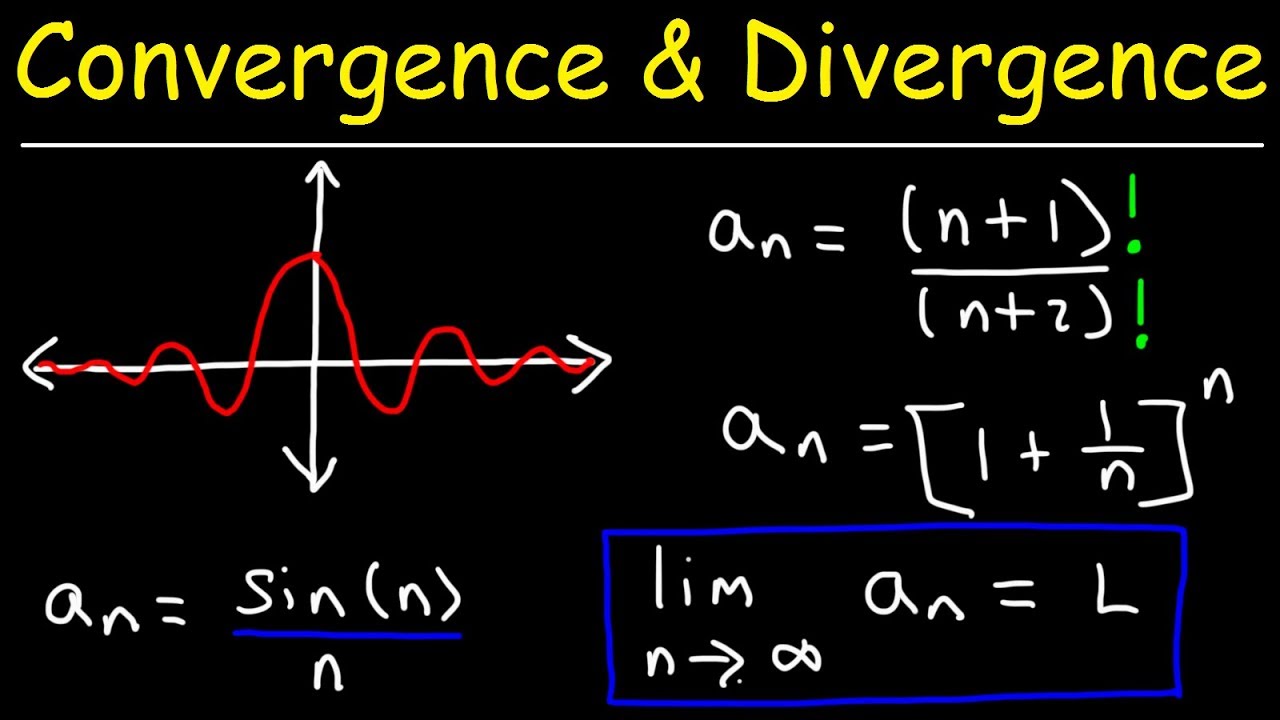
Professor Greist introduces the final chapter of the calculus course, focusing on sequences as a form of discrete calculus. He explains the difference between analog and digital functions, with sequences being digital input functions with an analog output. The professor emphasizes the ubiquity of sequences in various fields such as economics and digital signals. The lecture aims to re-evaluate sequences from the perspective of discrete calculus, starting with examples of interesting sequences, including polynomial-like, exponential, and trigonometric sequences. The concept of limits in the context of sequences is also introduced, with a focus on limits as n approaches infinity, which is a key concept in understanding the behavior of sequences.

05:03

🔍 Understanding Sequences and Their Limits

This paragraph delves deeper into the concept of limits for sequences. The professor explains the epsilon-N definition of a limit, which is applicable for sequences as n approaches infinity. The importance of limits in sequences is illustrated through examples like the Taylor series approximation of 'e' and Newton's method. The paragraph also explores the use of continuous methods to solve discrete problems, such as calculating the limit of a sequence using logarithms and Taylor series. The professor provides examples of sequences with polynomial and exponential growth, as well as more complex sequences that involve trigonometric functions and non-repeating behavior, highlighting the phenomenon of aliasing in fast-spinning objects.

10:04

🔢 Calculating Limits Using Recursion Relations

The third paragraph discusses the computation of limits for sequences that satisfy a recursion relation. The professor demonstrates how to apply the limit to a recursion relation to find the limit of a sequence, using algebraic manipulation and solving polynomial equations. Examples provided include sequences that involve nested square roots and the golden ratio, which is derived from a specific recursion relation. The paragraph also touches on the Fibonacci sequence and its relation to discrete calculus, suggesting further exploration of its mathematical properties in bonus material. The lecture concludes with a look forward to the next lesson, which will examine the discrete analog of the exponential function and its connection to derivatives.

Mindmap

Keywords

💡Calculus

Calculus is a branch of mathematics that deals with the study of rates of change and accumulation. In the context of this video, it refers to the transition from the continuous study of functions to the discrete study of sequences, which is a fundamental shift in perspective. The video discusses how calculus, traditionally focused on analog functions, can be reinvented for digital or discrete inputs, such as sequences.

💡Sequence

A sequence in mathematics is an ordered list of numbers or functions. In this video, sequences are presented as the discrete analog to functions, where the input is a natural number and the output is a real number. The concept of sequences is central to the theme of the video, as it explores how to apply calculus to these discrete inputs.

💡Discrete Calculus

Discrete calculus is a field that parallels traditional calculus but applies to discrete rather than continuous quantities. The video script introduces the concept of discrete calculus as a way to extend the methods and theories of calculus to sequences and other discrete inputs, which is a key theme of the lecture.

💡Analog Functions

Analog functions are those whose inputs and outputs vary continuously. The video contrasts analog functions with the discrete nature of sequences, highlighting the difference in how calculus is applied to these two types of mathematical objects. The script discusses how most of the course has focused on analog functions up to this point.

💡Limit

In calculus, a limit is the value that a function or sequence approaches as the input approaches some value. The video discusses the concept of limits in the context of sequences, specifically as the input approaches infinity. Limits are essential for understanding the behavior of sequences and are a central concept in the construction of discrete calculus.

💡Taylor Series

A Taylor series is an expansion of a function into an infinite sum of terms calculated from the values of the function's derivatives at a single point. The video mentions Taylor series in the context of approximating values, such as the number E, and as a method for computing limits, illustrating the connection between continuous and discrete approaches in calculus.

💡Polynomial Sequence

A polynomial sequence is one where the terms can be described by a polynomial expression. In the script, the sequence N squared is given as an example of a polynomial-like sequence, demonstrating how some sequences grow in a manner similar to polynomial functions.

💡Exponential Sequence

An exponential sequence is one where the terms grow at an exponential rate. The video provides the sequence 2 to the power of N as an example of an exponential sequence, contrasting it with polynomial sequences and illustrating the variety of growth behaviors in sequences.

💡Trigonometric Function

Trigonometric functions are mathematical functions relating to the angles of a triangle and are periodic in nature. The video script uses the cosine function as an example to describe a sequence that repeats in a wave-like pattern, but also introduces the concept of non-repeatability in sequences, such as 'cosine n', which never repeats.

💡Aliasing

Aliasing in the context of the video refers to the phenomenon where a rapidly spinning object appears to be spinning at a different rate or direction due to the limitations of the visual refresh rate. It is used as an analogy to describe non-repeating sequences that may appear to behave differently than expected.

💡Fibonacci Sequence

The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding ones, often starting with 0 and 1. The video mentions the Fibonacci sequence as an example of a sequence with interesting mathematical properties and suggests that calculus can provide insights into its behavior.

💡Golden Ratio

The golden ratio, denoted by the Greek letter phi (φ), is a mathematical constant approximately equal to 1.61803398875. It often appears in art, architecture, and nature. The video discusses the golden ratio in the context of a limit computation involving a recursive sequence, highlighting its significance in discrete mathematics.

Highlights

Introduction to the final chapter on sequences in the course, emphasizing the shift from analog to digital calculus.

Explanation of sequences as discrete input functions with an analog output, with natural numbers as inputs and reals as outputs.

The ubiquity of sequences in various fields such as economics and digital signals.

The notation for sequences, including writing out terms and the use of a sub n to denote the output for a given n.

The goal of recreating calculus concepts in a digital form for sequences.

Examples of sequences, including polynomial-like sequences and exponential sequences.

Description of a curious repeating sequence that resembles a trigonometric function.

Introduction of the concept of aliasing in the context of non-repeatable sequences.

The importance of taking limits in sequences, especially as n approaches infinity.

The use of continuous methods to solve discrete problems, illustrated with an example sequence.

The application of Taylor series and Big O notation in the discrete setting for evaluating limits.

A method to compute limits using recursion relations and algebraic manipulation.

The computation of a limit involving a nested square root sequence, leading to a quadratic equation.

The concept of the golden ratio and its relation to a specific sequence limit.

The Fibonacci sequence and its mathematical properties, hinting at further exploration in calculus.

The connection between the discrete calculus and the exponential function, setting the stage for the next lesson.

Transcripts

Browse More Related Video

Calculus Chapter 5 Lecture 46 Differences II

Calculus Chapter 5 Lecture 54 Power Series

Ch. 12.1 Sequences and Summation Notation

1. Signals and Systems

Calculus Chapter 5 Lecture 48 Numerical Odes II

Converging and Diverging Sequences Using Limits - Practice Problems