Why don't they teach Newton's calculus of 'What comes next?'
TLDRThe video delves into the fascinating world of sequence calculus, exploring the mysterious 'what's next' puzzles and revealing the hidden patterns within seemingly random sequences. By introducing the concept of differences and antidifferences, it bridges the gap between traditional calculus and this new realm of sequences. The video highlights the power of the Gregory-Newton interpolation formula in uncovering the underlying polynomial rules of sequences and emphasizes the practical applications of sequence calculus in real-world scenarios. It also touches on the geometric interpretations of sums and differences, drawing parallels with integral calculus. The content is rich with mathematical insights, offering viewers a new perspective on problem-solving and the beauty of mathematical patterns.
Takeaways
- 🔢 The video introduces a mathematical guessing game involving a sequence that appears random but arises naturally in mathematics.
- 🎯 The game involves identifying patterns in sequences, and the video challenges viewers to find another power of 2 in the given sequence.
- 📈 The video transitions from the guessing game to discussing the concept of 'calculus of sequences', which parallels the familiar calculus taught in schools.
- 🌐 In sequence calculus, sequences play the role of functions, differences play the role of derivatives, and sums play the role of integrals.
- 📚 The video explains how to use the Gregory-Newton interpolation formula to find a polynomial rule that fits a given sequence.
- 🔍 The process of finding the polynomial rule involves creating a difference scheme and using the Gregory-Newton formula to reconstruct the original sequence.
- 🌟 The video demonstrates the formula's application by solving a 'what's next' riddle involving the mathematical constants pi, phi, and e.
- 💡 The video highlights the beauty of mathematics by showing how the Gregory-Newton formula can be used to solve complex sums and find areas under curves.
- 🧩 The video pieces together the connections between school calculus and sequence calculus, showing that everything in school calculus has a counterpart in sequence calculus.
- 📊 The video provides insights into how sequence calculus can be applied to real-life numerical problems, such as approximating areas under curves using polynomial approximations.
- 🎓 The video concludes with a proof of the Gregory-Newton formula, showing its effectiveness in reconstructing a sequence from its difference scheme.
Q & A
What is the main topic of the Mathologer video discussed in the transcript?
-The main topic of the video is the exploration of sequence calculus, specifically focusing on the Gregory-Newton interpolation formula and its applications in solving 'what's next' puzzles and understanding various mathematical sequences.
How does the video introduce the concept of sequence calculus?
-The video introduces sequence calculus by drawing parallels with familiar concepts in standard calculus. It explains that sequences play the role of functions, differences play the role of derivatives, sums play the role of integrals, and difference equations mirror differential equations.
What is the significance of the sequence 1, 2, 4, 8, 16 in the video?
-The sequence 1, 2, 4, 8, 16 is used as an example of a mystery sequence that initially appears to follow a pattern (powers of 2) but then deviates, leading to a discussion on how to discover hidden patterns in sequences.
What is the role of the bottom row of 1s in the difference scheme?
-The bottom row of 1s in the difference scheme is significant because it helps in reconstructing the entire difference scheme and understanding the pattern of the original sequence.
How does the video demonstrate the concept of differences in sequence calculus?
-The video demonstrates the concept of differences by showing how the difference of the sequence (the second row) is the slope of the line segments in the diagram, analogous to the derivative of a function in standard calculus.
What is the Gregory-Newton interpolation formula mentioned in the video?
-The Gregory-Newton interpolation formula is a method for finding a polynomial rule that fits a given sequence. It is a significant part of the video's discussion on sequence calculus and its applications.
How does the video connect the concept of sequence calculus to real-world problems?
-The video suggests that real-world calculus problems are often solved using sequence calculus, as it provides a systematic approach to understanding and manipulating sequences, which can be applied to various practical situations.
What is the significance of the 'falling powers' in the context of sequence calculus?
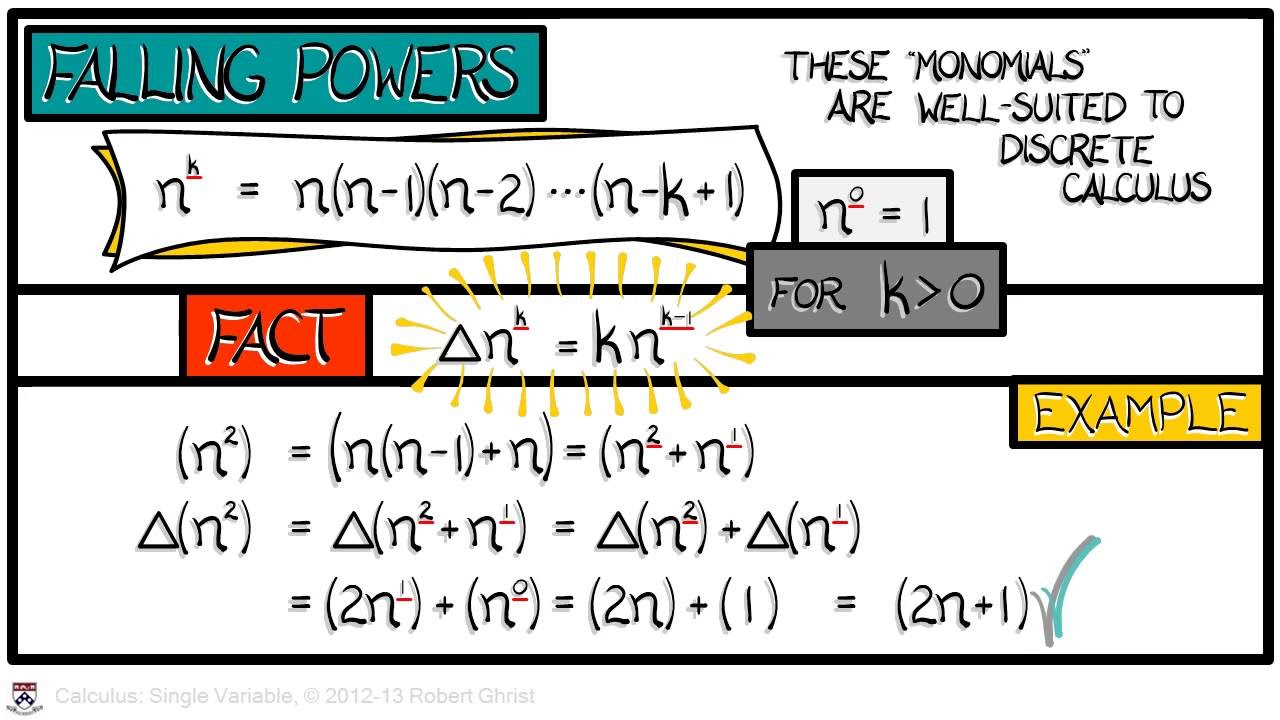
-Falling powers are special products that behave similarly to normal powers in terms of differencing. They are introduced as counterparts to the nth powers in school calculus and are used to express things in sequence calculus, providing a fix for the fact that differences of normal powers don't behave as nicely as their derivatives.
How does the video use the concept of anti-differentiation in sequence calculus?
-Anti-differentiation in sequence calculus is used to find formulas for the sums of sequences. The video demonstrates this by showing how to extend a difference scheme going up and then using the Gregory-Newton formula to find the sum of the squares.
What is the fundamental theorem of sequence calculus, and how does it relate to the fundamental theorem of calculus?
-The fundamental theorem of sequence calculus states that every sequence has a unique difference scheme up to a constant, and every difference scheme corresponds to a unique sequence. This theorem mirrors the fundamental theorem of calculus, which deals with functions and their derivatives and integrals.
How does the video explain the geometric interpretation of sums in sequence calculus?
-The video explains that the sums in sequence calculus can be interpreted geometrically as the areas under a staircase formed by the sequence values. This is analogous to how antiderivatives in standard calculus are used to find areas under curves.
Outlines
🧩 Introduction to Sequences and Guessing Games
The video begins with an introduction to a familiar mathematical guessing game, where the first few terms suggest a pattern of powers of 2. However, the sequence quickly becomes less predictable. The speaker introduces a method for deciphering such sequences by calculating differences between consecutive terms. This method reveals a hidden pattern of 1s, suggesting a connection to powers of 2. The video sets the stage for exploring the mathematics behind 'what's next' puzzles and introduces the concept of sequence calculus as a way to systematically solve these puzzles.
📚 Understanding Sequences through School Calculus
The speaker explains how to approach sequences using the concept of functions from school calculus, with the original sequence represented as a function f. The introduction of a 0th term leads to the idea of graphing sequences and the concept of differences as slopes of line segments, drawing parallels with derivatives in calculus. The video also introduces the idea of higher differences and the potential for reconstructing sequences from partial information. The speaker then provides examples of differencing simple sequences like powers of 2 and squares, highlighting the similarities and differences from standard calculus.
🔢 Algebraic Patterns and Polynomial Sequences
This paragraph delves into the algebraic patterns found in sequences, particularly focusing on polynomial sequences. The speaker discusses the properties of difference schemes for sequences like squares and cubes, and how these relate to familiar mathematical concepts like factorials. The video also introduces rules for manipulating difference schemes, such as the effect of multiplying a sequence by a constant or adding two sequences together. The speaker emphasizes that all polynomial sequences result in constant rows in their difference schemes, hinting at the nature of the mystery sequence introduced earlier.
🤔 Solving 'What's Next' Riddles and the Gregory-Newton Formula
The speaker introduces the Gregory-Newton interpolation formula as a powerful tool for solving 'what's next' riddles and finding the underlying polynomial rule of a sequence. The video demonstrates the application of the formula to the mystery sequence from the introduction, showing how it can accurately predict the next terms. The speaker also discusses the broader implications of the formula, including its ability to handle an infinite number of terms and its application to non-integer values, highlighting the beauty and utility of the Gregory-Newton formula in sequence calculus.
🌟 Insights and Applications of the Gregory-Newton Formula
The speaker provides a deeper exploration of the Gregory-Newton formula, offering insights into its applications and connections to other mathematical concepts. The video discusses how the formula can be used to solve any 'what's next' puzzle, even with non-traditional sequences like pi, phi, and e. The speaker also touches on the limitations of such puzzles and the importance of scientific context in truly understanding sequences. The video concludes with a promise to provide the mathematical context for the mystery sequence in a future segment.
🎲 The Fibonacci Sequence and Difference Equations
The speaker shifts focus to the Fibonacci sequence, exploring its difference scheme and how it mirrors the sequence itself. The video highlights the geometric and algebraic properties of the sequence, leading to the formulation of a difference equation. The speaker then connects this to the concept of solving differential equations, showing that the Fibonacci sequence can be solved in a manner similar to linear second-order homogeneous differential equations. The video concludes with a teaser for the proof of the Gregory-Newton formula and its application in real-life numerical calculations.
📈 Proof of the Gregory-Newton Formula and Sequence Calculus
The speaker provides a sketch of the proof for the Gregory-Newton formula, focusing on sequences that end in a constant row. The video uses the example of n choose 4 to illustrate how the formula works and how it can be extended to other sequences. The speaker also discusses the broader implications of sequence calculus, drawing parallels with school calculus and highlighting the fundamental theorem of sequence calculus. The video concludes with a challenge for the viewer to prove the fundamental theorem themselves and a brief overview of how sequence calculus can be applied to real-life numerical problems.
Mindmap
Keywords
💡Mathologer
💡sequence
💡difference
💡calculus
💡Gregory-Newton interpolation formula
💡Pascal's triangle
💡Fibonacci sequence
💡binomial coefficients
💡Maclaurin series
💡antidifferentiation
Highlights
The video introduces a mathematical guessing game involving a sequence that appears random but arises naturally in mathematics.
The sequence starts with the first five terms being powers of 2, but then the pattern breaks down and the numbers seem random.
By subtracting consecutive terms of the sequence, a hidden pattern of all 1s is revealed, suggesting a key to the sequence's pattern.
The video challenges viewers to find another power of 2 in the sequence and to identify a pattern where the powers of 2 occur.
The video introduces the concept of 'calculus of sequences', a parallel universe to the familiar calculus taught in schools, where sequences play the role of functions.
In the calculus of sequences, differences play the role of derivatives, sums play the role of integrals, and difference equations mirror differential equations.
The video provides a crash course in the calculus of sequences and its applications, including the Gregory-Newton interpolation formula.
The video explains that the difference of the powers of 2 is again the powers of 2, drawing a parallel to the exponential function e^x being its own derivative in standard calculus.
The difference of the sequence of squares (n^2) results in the sequence of odd numbers, and the second difference is the constant number 2.
The video demonstrates that the difference schemes of all polynomial sequences end in constant rows, and that polynomial sequences are the ones that result in constant rows.
The video introduces the Gregory-Newton interpolation formula as a way to find a polynomial rule that fits a given sequence.
The video shows how the Gregory-Newton formula can be used to 'solve' any 'what's next' riddle, providing an example with the mathematical constants pi, phi, and e.
The video emphasizes that the 'what's next' game is fundamentally flawed unless the answer can be justified within a proper scientific context.
The video provides the mathematical context for the mystery sequence, showing that it is related to the maximum number of regions that can be formed by connecting pairs of dots on a circle.
The video explains how the Gregory-Newton formula can be used to find formulas for the sums of sequences, providing an example with the sum of squares.
The video discusses the concept of falling powers in sequence calculus, which behave similarly to normal powers in terms of differencing.
The video shows that the Gregory-Newton formula for 2^n works for any positive real number, not just non-negative integers, and can be used to approximate root 2.
The video highlights the fundamental theorem of sequence calculus, drawing parallels with the fundamental theorem of calculus from school mathematics.
The video concludes with a sketch of a proof for the Gregory-Newton formula, showing its effectiveness for sequences whose difference schemes end in a constant row.
Transcripts
Browse More Related Video
Calculus Chapter 5 Lecture 46 Differences II
Introduction to Sequences (Precalculus - College Algebra 67)

Math Antics - Number Patterns

Calculus 2 Lecture 9.1: Convergence and Divergence of Sequences

Arithmetic Sequences (Precalculus - College Algebra 69)
Geometric Sequences (Precalculus - College Algebra 71)
5.0 / 5 (0 votes)
Thanks for rating: