Calculus Chapter 1 Lecture 1 Functions

Penn Online Learning
23 Jun 201615:54
EducationalLearning
32 Likes 10 Comments

TLDRProfessor Greist introduces the foundational concepts of calculus through the lens of functions, emphasizing their roles in mathematical narratives. He explains the domain and range, composition, and inverse functions, with examples like the square root of 1 minus x squared. The lecture delves into polynomials, rational functions, and the importance of understanding fractional and irrational powers. Trigonometric, inverse trigonometric, and exponential functions are highlighted, with a special focus on the mysterious and fundamental constant 'e', setting the stage for deeper exploration in subsequent lessons.

Takeaways
  • 📚 The lecture introduces the concept of functions as the central theme in calculus, emphasizing their role in mathematical interactions and characterizations.
  • 🔍 Functions are described both graphically and mechanistically, with the domain as all possible inputs and the range as all possible outputs.
  • 🔗 Composition of functions is a critical operation, where one function's output is used as the input for another, denoted as F(G(x)).
  • 🔄 The inverse function is introduced as a concept that 'undoes' the original function, with the notation f^(-1)(x).
  • 📈 Polynomials are highlighted as a fundamental class of functions, characterized by their degree and expressed using summation notation.
  • 📉 Rational functions are presented as another common class, defined as the ratio of two polynomials, with caution advised when the denominator approaches zero.
  • 👁 Fractional and irrational powers of x are discussed, including their geometric interpretations and implications for function behavior.
  • 🌀 Trigonometric functions are identified as essential in calculus, with a focus on the Pythagorean identity and the unit circle's role in their definitions.
  • ↔️ Inverse trigonometric functions are introduced, with a preference for using 'arc' notation to avoid confusion with reciprocal functions.
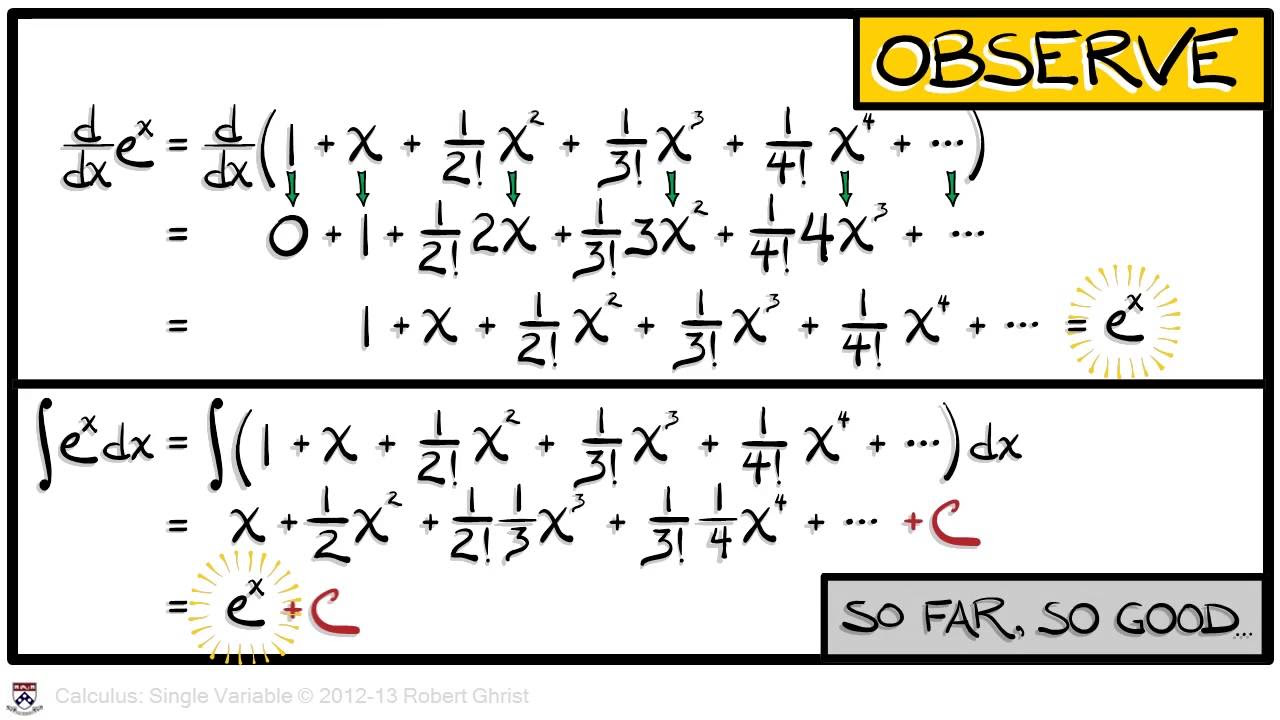
  • 📊 Exponential functions are characterized by their base 'e' and their unique properties, including being their own derivative and integral.
  • 🧬 Euler's formula is introduced as a mysterious yet fundamental concept linking exponential functions with trigonometric functions, involving the imaginary unit 'i'.
Q & A

  • What is the main focus of the calculus course as described in the script?

    -The main focus of the calculus course is on functions, their interactions, and their characteristics, including local behaviors and global asymptotics.

  • How is a function typically visualized in the context of this script?

    -A function is visualized as a machine where 'X' is the input and 'f(X)' is the output.

  • What is the domain of a function?

    -The domain of a function consists of all possible inputs that can be put into the function.

  • What is the range of a function?

    -The range of a function consists of all possible outputs that can be received from the function.

  • What is function composition and how is it denoted?

    -Function composition is the operation where one function takes the output of another function as its input. It is denoted as 'F composed with G of X' or 'F(G(X))'.

  • Can you provide an example of a function and its decomposition into the composition of two functions F and G?

    -The function 'square root of (1 - x^2)' can be decomposed into the composition of F and G, where G(x) = 1 - x^2 and F is the square root function.

  • What is the inverse of a function and how is it denoted?

    -The inverse of a function 'f' is denoted as 'f^(-1)' and it is the function that takes an input 'X' and returns 'f^(-1)(X)' such that when composed with 'f', it gives back the original value of 'x'.

  • What is the inverse function of 'X cubed'?

    -The inverse function of 'X cubed' is 'X to the 1/3 power' or the cube root of 'x'.

  • What are polynomials and how are they represented in summation notation?

    -Polynomials are functions of the form 'a constant plus a constant times X plus a constant times X squared' up to a finite degree. They are represented in summation notation as 'Σ (C_K * X^K) from K=0 to N', where 'C_K' are coefficients.

  • What are rational functions and what do they look like?

    -Rational functions are functions of the form 'P(X) / Q(X)', where 'P' and 'Q' are polynomials. An example is '(3X - 1) / (X^2 + X - 6)'.

  • Why are trigonometric functions important in calculus?

    -Trigonometric functions are important in calculus due to their prevalence in various mathematical and real-world applications, as well as their unique properties, such as the Pythagorean identity 'cos^2(θ) + sin^2(θ) = 1'.

  • What is Euler's formula and what does it relate?

    -Euler's formula states that 'e^(iθ) = cos(θ) + i*sin(θ)'. It relates the exponential function with imaginary unit 'i' to trigonometric functions.

  • What is the significance of the number 'e' in mathematics, particularly in the context of exponential functions?

    -The number 'e' is significant as it is the base of the natural logarithm and is the value whose logarithm is equal to 1. It is also the unique number such that the derivative of 'e^x' is 'e^x' itself, making it fundamental in calculus.

Outlines
00:00
📚 Introduction to Calculus and Functions

Professor Greist begins the calculus course by introducing the fundamental concept of functions as the main characters in the calculus narrative. Functions are described from both a graphical perspective, where they are represented as graphs, and a mechanistic one, where inputs are transformed into outputs. The professor explains key function terminology such as domain and range, and introduces the concept of function composition, where one function is applied after another. He also discusses the inverse of a function, which is the 'undoing' of a function's effect, using the example of the cube root being the inverse of cubing a number.

05:03
🔍 Exploring Function Classes and Operations

The script delves into various classes of functions, starting with polynomials, which are sums of terms involving powers of the variable x with constant coefficients. Rational functions, which are ratios of polynomials, are also highlighted, with a caution about undefined behavior when the denominator is zero. The discussion continues with non-integer powers, including roots and reciprocals, and then moves to trigonometric functions, emphasizing the Pythagorean identity. The properties and interpretations of trigonometric functions, such as sine and cosine, are reviewed, along with their inverses, which have restricted domains.

10:04
📉 Asymptotes and the Mystique of Exponential Functions

The script addresses functions with vertical asymptotes, such as those involving ratios that become undefined when the denominator is zero. It then transitions to the importance of exponential functions, particularly the function e^x, which has unique properties including being its own derivative and integral. The professor introduces Euler's formula, which connects exponential functions with trigonometric functions through the imaginary unit i, and hints at the significance of the number e, which will be explored further in the next lesson.

15:07
🌟 The Enigma of the Exponential Function

The final paragraph wraps up the script with an intriguing note on the exponential function, specifically the mystery surrounding the number e. While e is known for its unique mathematical properties, such as its relationship with the natural logarithm, the professor leaves the audience with a question about the true meaning and significance of e, promising to delve deeper into this in the subsequent lesson.

Mindmap
Keywords
💡Functions
Functions are the central theme of calculus and the video script emphasizes their importance by describing them as the 'cast of characters' in the 'story of calculus.' A function, in mathematical terms, is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. In the script, functions are introduced with the mechanistic view of an input-output model, where 'X' is fed into 'F' to produce 'f(X)'. This concept is foundational for understanding the interactions and behaviors of functions throughout the course.
💡Domain
The domain of a function is the set of all possible inputs for that function. In the script, it is mentioned as the 'all possible inputs' that one can put into a function. The domain is crucial for defining the scope within which a function operates and is particularly important in single-variable calculus where it often consists of real numbers or subsets of the real number line.
💡Range
The range of a function is the set of all possible outputs or values that the function can produce. It is defined in the script as 'all possible outputs' that one might receive from a function 'F'. The range is significant for understanding the behavior of a function and its possible values, which in single-variable calculus, like the domain, is often the real number line or a subset of it.
💡Composition
Function composition is a critical operation where one function is applied after another. In the script, it is denoted as 'F composed with G of X', which is described as 'G(X) fed into the function F'. This operation is visualized as 'chaining together' the functions in a specific order, where the output of one function becomes the input of the next, and it is essential for understanding how functions interact.
💡Inverse
The inverse of a function, denoted as 'F^(-1)' in the script, is a function that 'undoes' what the original function does. It is defined such that when composed with the original function, it returns the original input value. The script uses the example of the inverse of 'X cubed' being 'X to the 1/3 power', illustrating the concept of reversing the roles of input and output to achieve the inverse relationship.
💡Polynomials
Polynomials are a class of functions that are sums of powers of 'X' with coefficients. They are defined in the script as functions of the form 'a constant plus a constant times X, plus a constant times X squared, up to some finite degree'. The degree of a polynomial is the highest power of 'X' present. Polynomials are fundamental in calculus and are often represented using summation notation, as in 'Σ C_K * X^K'.
💡Rational Functions
Rational functions are another class of functions that are the ratio of two polynomials, as described in the script with the example '3X - 1 over X squared + X - 6'. They are important in calculus and have applications in various mathematical fields. However, the script cautions about the undefined nature of rational functions when the denominator is zero.
💡Trigonometric Functions
Trigonometric functions, such as sine and cosine, are prevalent in calculus and are mentioned in the script with the fundamental identity 'cosine squared plus sine squared equals 1'. They are related to the geometry of a unit circle and have various interpretations, including their connection to right triangle ratios and the equation of a circle.
💡Exponential Functions
Exponential functions, exemplified by 'e to the X' in the script, are functions where the variable is in the exponent. They have unique properties, such as being their own derivative and integral. The script introduces 'e' as a base of these functions and hints at its significance, which will be explored further in the course.
💡Euler's Formula
Euler's formula, as mentioned in the script, is a profound mathematical statement that connects exponential functions with trigonometric functions. It is given by 'e^(iX) equals cosine of X plus i times sine of X'. The script introduces this formula as a mystery that will be unraveled in subsequent lessons, indicating its importance in understanding complex numbers and their exponential representation.
Highlights

Introduction to the concept of functions as the central theme of calculus.

Explanation of functions in terms of their graphs and mechanistic view as input-output relationships.

Definition of domain and range of a function in the context of single-variable calculus.

Importance of function composition and its notation, F composed with G of X.

Visualizing function composition as chaining functions F and G in sequence.

Decomposition of the square root of 1 minus x squared into the composition of functions F and G.

Introduction to the concept of inverse functions and their mathematical notation.

Example of finding the inverse of the function f(x) = x cubed, resulting in the cube root.

Discussion on the significance of polynomials and their representation using summation notation.

Introduction to rational functions, their definition, and potential issues with denominators.

Explanation of non-integer powers of x, including fractional and negative exponents.

Overview of trigonometric functions, their identities, and geometric interpretations.

Clarification on inverse trigonometric functions and the correct notation to avoid confusion.

Importance of exponential functions, their properties, and their role in calculus.

Introduction to Euler's formula and its relation to exponential functions with imaginary numbers.

Mystery surrounding the value of e and its significance in exponential functions.

Algebraic properties of exponential functions, including multiplication and exponentiation rules.

Differential and integral properties of the exponential function e to the x, being its own derivative and integral.

Transcripts

Browse More Related Video

Calculus Chapter 1 Lecture 2 Exponentials

Finding Inverse Functions (Precalculus - College Algebra 51)

Calculus Chapter 2 Lecture 16 d As Operator

Precalculus Introduction, Basic Overview, Graphing Parent Functions, Transformations, Domain & Range

Calculus Chapter 2 Lecture 10 Derivatives

Calculus Chapter 1 Lecture 9 Orders of Growth

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus BasicsFunction TheoryTrigonometric IdentitiesInverse FunctionsPolynomialsRational FunctionsExponential FunctionsNatural LogarithmEuler's FormulaEducational ContentMathematics LectureFunction CompositionDomain and RangeAlgebraic PropertiesDifferential PropertiesIntegral PropertiesImaginary NumbersTrigonometric FunctionsInverse Trigonometry