Calculus Chapter 2 Lecture 10 Derivatives
TLDRIn this calculus lecture, Professor Greist explores the concept of derivatives beyond the traditional interpretation of slopes, emphasizing their broader significance in various fields. He introduces and compares three definitions of the derivative, illustrating each with examples like polynomials, exponential functions, and trigonometric functions. The lecture highlights derivatives' ubiquity in physics, economics, and engineering, showcasing their importance in rates of change and beyond.
Takeaways
- 📚 The lecture introduces the concept of derivatives and their interpretations beyond just slopes, emphasizing their broader significance in various contexts.
- 🔍 Derivatives are differentiated from their interpretations, with the lecture focusing on the definitions that underpin their understanding.
- 🤔 The traditional interpretation of derivatives as slopes is challenged, as it is not universally applicable, especially in multivariable calculus.
- 📈 Three definitions of the derivative are presented, each offering a unique perspective on how the rate of change of a function is conceptualized.
- 📝 The first definition of the derivative is framed as a limit of the change in output over the change in input, highlighting its conceptual clarity.
- 📉 The second definition, using a change of variables, is shown to be essentially the same as the first, with the focus on the limit as the change in input approaches zero.
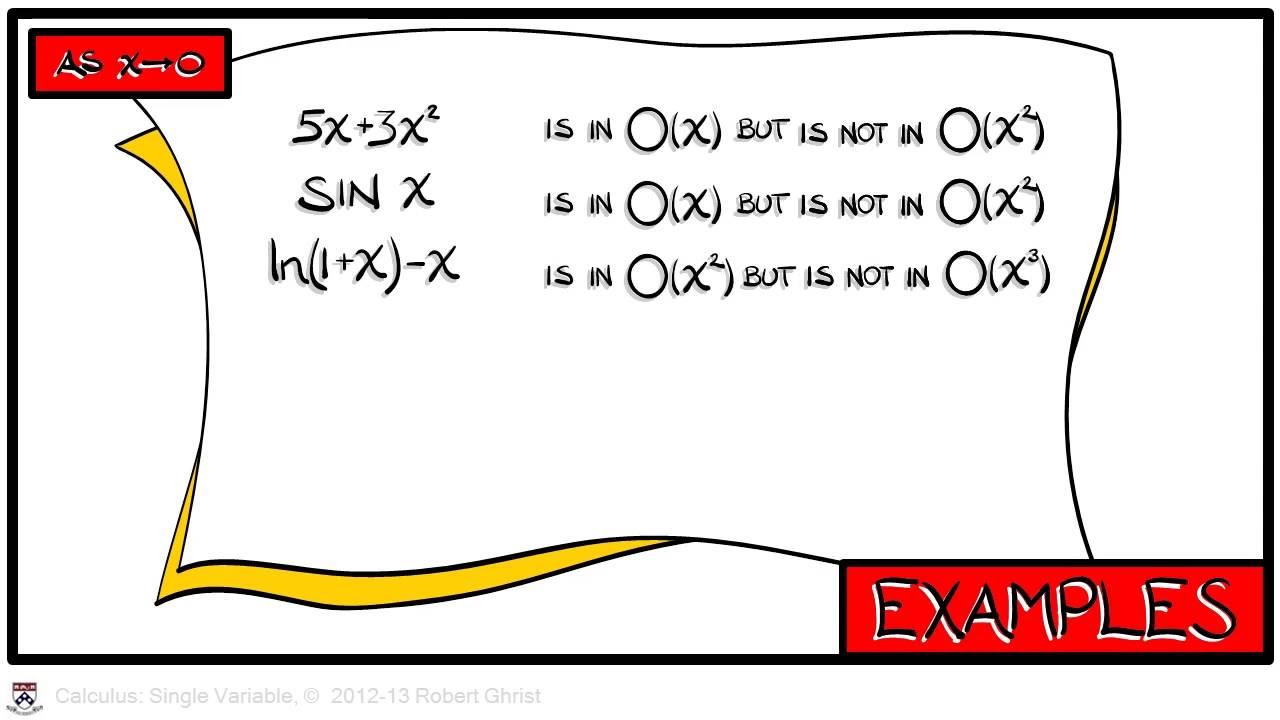
- 📊 The third definition introduces the concept of the first-order variation of the output, defining the derivative as the constant coefficient in front of the first-order term in a Taylor expansion.
- 🌟 Examples are used to illustrate the computation of derivatives for functions like \( f(x) = x^n \), \( e^x \), \( \cos(x) \), and \( \sqrt{x} \), demonstrating the application of the definitions.
- 📚 Notation for derivatives is discussed, with a focus on clarity and avoiding confusion with other mathematical symbols.
- 🚀 Derivatives are shown to be applicable in various fields, including physics, chemistry, economics, and more, underlining their ubiquity and importance.
- 🔑 The lecture concludes by emphasizing the importance of understanding the proper definition of derivatives for their correct interpretation and application.
Q & A
What is the main focus of the lecture on derivatives?
-The lecture focuses on the interpretation and definition of derivatives, distinguishing between the concept of slope as a poor interpretation and exploring the actual meanings of derivatives in various mathematical contexts.
Why is the concept of slope not the definition of a derivative according to the lecture?
-Slope is considered a poor interpretation of a derivative because it does not apply to functions with multiple inputs and outputs, or to functions that are not smooth enough to have a well-defined slope.
What are the three definitions of the derivative presented in the lecture?
-The three definitions are: 1) The limit as X approaches a of (f(X) - f(a)) / (X - a), 2) The limit as h approaches 0 of (f(a + h) - f(a)) / h, and 3) The constant C in the first-order term of the Taylor expansion of f(a + h).
How does the lecture explain the first definition of the derivative?
-The first definition is explained as the limit of the change in the output over the change in the input as the input approaches a certain value.
What is the significance of the second definition of the derivative in the lecture?
-The second definition is significant because it provides a familiar interpretation of the derivative as the limit of the change in output over the change in input as the change in input approaches zero.
What does the third definition of the derivative involve?
-The third definition involves the first-order variation of the output, where the derivative is defined as the constant coefficient in front of the first-order term in the Taylor expansion of the function evaluated at a plus h.
How does the lecture illustrate the computation of derivatives using the binomial theorem?
-The lecture uses the binomial theorem to simplify the computation of derivatives for functions like f(X) = X^n, showing how the terms involving powers of h cancel out or become negligible as h approaches zero.
What are some examples of functions discussed in the lecture to illustrate the computation of derivatives?
-Examples include e^X, cosine(X), and the square root of X, where the derivatives are computed by evaluating the functions at X plus h and simplifying using the binomial theorem or other mathematical properties.
Why is the notation 'dy/dx' considered the best for denoting derivatives?
-'dy/dx' is considered the best notation because it clearly indicates the rate of change of Y with respect to a change in X, making it explicit which variables are involved.
What are some common misconceptions about derivatives that the lecture aims to clarify?
-The lecture clarifies that derivatives are not just about slopes and are not limited to rates of change with respect to time. It emphasizes that derivatives are ubiquitous and can be found in various fields beyond physics, such as economics, chemistry, and engineering.
How does the lecture connect the concept of derivatives to real-world applications?
-The lecture connects derivatives to real-world applications by mentioning examples such as velocity, acceleration, current, reaction rates, spring constants, elastic modulus, viscosity, and marginal tax rates, all of which are defined in terms of rates of change.
Outlines
📚 Introduction to Derivatives and Their Interpretations
Professor Greist introduces the concept of derivatives in calculus, emphasizing the distinction between the interpretation and definition of a derivative. The lecture aims to clarify that derivatives are more than just slopes, and they are applicable in various contexts, including multivariable calculus and non-smooth functions. Three definitions of the derivative are discussed: the limit definition, the change in output over input, and the first-order variation of the output. The professor also touches on the importance of understanding derivatives beyond their slope interpretation.
🔍 Exploring Derivative Definitions with Examples
This section delves deeper into the definitions of derivatives by examining specific examples, such as the function f(x) = x^n. The professor demonstrates how the derivative can be computed using the limit as h approaches zero and how it relates to the first-order variation of the output. The discussion includes the binomial theorem and the simplification of higher-order terms as Big O of h squared. The examples serve to illustrate the application of the derivative definitions in various mathematical contexts.
📈 Derivatives of Common Functions and Notation
The script continues with the computation of derivatives for common functions like e^x, cosine(x), and the square root of x. The professor uses the first-order variation method to determine the derivatives and highlights the importance of proper notation when dealing with derivatives. The section also clarifies the difference between various notations such as dy/dx and f'(x), emphasizing the need to maintain clarity and avoid ambiguous or incorrect notation.
🌐 Applications of Derivatives in Various Fields
In this final paragraph, the professor broadens the scope of derivatives beyond mathematics to their applications in physics, chemistry, economics, and engineering. Examples include velocity and acceleration in physics, reaction rates in chemistry, spring constants and elastic modulus in materials science, and marginal tax rates in economics. The paragraph concludes with an encouragement to recognize the ubiquity of derivatives in everyday phenomena and the importance of understanding their definitions for practical use.
Mindmap
Keywords
💡Derivative
💡Differentiation
💡Limit
💡Slope
💡Multivariable Calculus
💡First-Order Variation
💡Taylor Expansion
💡Big O Notation
💡Binomial Theorem
💡Elastic Modulus
💡Marginal Tax Rates
Highlights
Introduction to the concept of derivatives beyond just slopes, emphasizing their broader mathematical and practical significance.
Differentiation between the interpretation and definition of a derivative, highlighting the importance of understanding the underlying principles.
Explanation of the derivative as the limit of the change in output over the change in input, providing a foundational definition.
Introduction of three different definitions of the derivative, offering a comprehensive understanding of its mathematical representation.
Clarification that slope is an interpretation of the derivative, not its definition, especially in contexts where slope is not well-defined.
Discussion on the derivative in multivariable calculus, where functions have multiple inputs and outputs, expanding the concept beyond single-variable functions.
Use of the limit process to define the derivative, emphasizing the conceptual clarity it provides in understanding rate of change.
Illustration of the derivative computation for the function f(x) = x^n, demonstrating the application of the binomial theorem.
Introduction of the first-order variation definition of the derivative, explaining it in terms of the function's output perturbation.
Comparison of different definitions using the example of f(x) = x^n, to show the equivalence and computation process.
Derivation of the derivative for exponential functions, e^x, using the first-order variation method.
Explanation of the derivative for trigonometric functions, specifically cosine, using the summation formula and its properties.
Derivation of the derivative for the square root function, involving simplification and application of the binomial theorem.
Discussion on the notation used for derivatives, emphasizing the importance of clarity and standardization in mathematical communication.
Highlighting the misuse of notation and the importance of adhering to standard derivative notation to avoid confusion.
Examples of derivatives in physics, such as velocity and acceleration, as rates of change with respect to time.
Application of derivatives in other fields like chemistry, economics, and engineering, showcasing their ubiquity and importance.
Encouragement to observe derivatives in everyday phenomena, emphasizing their relevance and the value of understanding their definition.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: