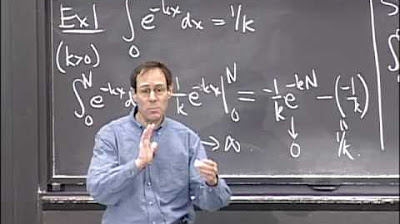Calculus Chapter 1 Lecture 9 Orders of Growth
TLDRIn this calculus lecture, Professor Greist introduces the concept of asymptotics and Big O notation to describe the growth rates of functions as they approach infinity or zero. He illustrates the hierarchy of growth, from constant functions to exponential growth, and beyond, with examples like monomials, exponential functions, and logarithms. The lecture also covers how to apply Big O notation to analyze the dominant terms in functions and the rules for combining functions with different growth rates, setting the stage for a deeper understanding of derivatives.
Takeaways
- 📚 The lecture introduces the concept of asymptotics, which is the study of how functions behave when they approach very large or very small values.
- 📈 The script discusses the rates at which different types of functions grow to infinity or approach zero, highlighting the hierarchy of growth from polynomial to exponential and beyond.
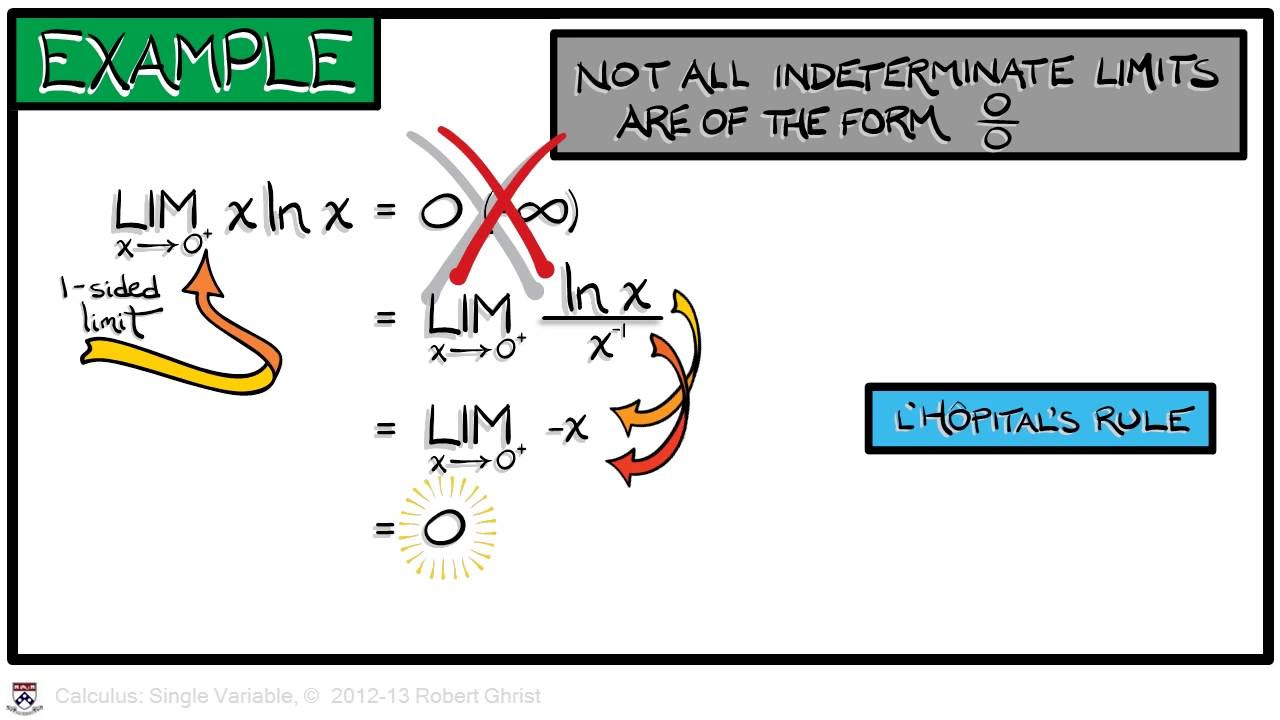
- 🔍 L'Hôpital's rule is used to compare the growth rates of exponential functions and monomials, showing that exponential functions grow faster than polynomials.
- 📉 The natural logarithm function, when raised to a power, grows slower than linear functions, indicating a hierarchy of growth rates even among different forms of the same type of function.
- 🌐 The script establishes a hierarchy of functional growth, starting with constant functions, moving to logarithmic, linear, quadratic, and so on up to exponential growth, and beyond with factorial growth.
- 🔑 The Big O notation is introduced as a language to describe the upper bounds of the growth rates of functions, with two forms: one for functions approaching infinity and another for those approaching zero.
- 🔍 The importance of the limit direction (towards infinity or zero) is emphasized, as it affects which terms in a function dominate and thus the function's growth rate.
- 📝 The script provides examples of how to apply Big O notation to various functions, including polynomials, logarithms, and exponential functions, to describe their growth or decay.
- 📚 The rules of asymptotic analysis are outlined, including how to handle multiplication and addition of functions within the Big O notation, affecting the resulting growth rate.
- 🔧 The script uses examples to demonstrate the application of Big O notation, showing how to simplify expressions and understand the dominant terms as functions approach certain limits.
- 🚀 The lecture concludes by connecting the concepts of asymptotics and growth rates to the upcoming topic of derivatives, setting the stage for further exploration in calculus.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the study of asymptotics, specifically focusing on orders of growth in functions as they approach very small or very large values.
What does the Big O notation represent in the context of this lecture?
-The Big O notation represents an upper bound on the growth rate of a function, providing a way to describe and compare the rates at which functions grow or approach zero.
How does the growth rate of an exponential function compare to that of a monomial?
-The exponential function grows faster than any monomial or polynomial function. This is demonstrated by applying L'Hôpital's rule and showing that the derivative of the exponential function eventually outpaces that of the monomial.
What is the hierarchy of functional growth as X approaches infinity?
-The hierarchy of functional growth as X approaches infinity starts with constant functions, then moves to logarithmic growth, followed by linear, quadratic, cubic, and so on, up to exponential growth and beyond, such as factorial growth.
How does the behavior of functions change as X approaches zero compared to when X approaches infinity?
-As X approaches zero, higher order terms dominate, with X to the power of n+1 being less than X to the power of N. Conversely, as X approaches infinity, lower order terms dominate, with X to the power of n+1 being greater than X to the power of N.
What is the definition of a function being in Big O of X to the N?
-A function f is said to be in Big O of X to the N if there exists a constant C such that the absolute value of f(X) is less than C times X to the N, indicating an upper bound on the growth of the function.
How does the concept of Big O notation apply to the Taylor series expansion of arctan(X)?
-In the Taylor series expansion of arctan(X), the first term is X, and all other terms are of higher order in X. Thus, we can say that arctan(X) is Big O of X squared, indicating that the growth of the function is dominated by the X term and the higher order terms are less significant.
What is the difference between the behavior of the function 5x + 3x^2 as X approaches zero and as X approaches infinity?
-As X approaches zero, the function 5x + 3x^2 is dominated by the 5x term, making it Big O of X. As X approaches infinity, the 3x^2 term dominates, and the function is not in Big O of X squared, indicating a faster growth rate.
How can the rules of Big O notation be applied when adding or multiplying functions?
-When multiplying functions, if one is in Big O of X to the M and the other is in Big O of X to the N, the result is in Big O of X to the M plus N. When adding functions, the resulting function is in Big O of the minimum of M and N as X approaches zero, and in Big O of the maximum of M and N as X approaches infinity.
What is an example of a function that grows faster than any polynomial function?
-An example of a function that grows faster than any polynomial function is the exponential function, such as e^X, which demonstrates faster growth as X approaches infinity.
How does the script illustrate the importance of the direction of the limit when analyzing the growth of functions?
-The script emphasizes that the direction of the limit (whether X is approaching zero or infinity) significantly affects the analysis of a function's growth, as it determines which terms dominate and thus the overall behavior of the function.
Outlines
📚 Introduction to Asymptotics and Big O Notation
Professor Greist begins lecture 9 by introducing the concept of asymptotics, which is the study of how functions behave as they approach infinity or near zero. The focus is on the rates at which functions grow or shrink, and how to quantify these changes using Big O notation. The lecture provides examples of different functions, such as monomials and exponential functions, to illustrate varying rates of growth. The concept of derivatives and L'Hôpital's rule is briefly touched upon to compare the growth rates of different types of functions, emphasizing that exponential functions grow faster than polynomials and monomials, and that linear growth outpaces logarithmic growth. The lecture sets the stage for understanding the hierarchy of functional growth and the importance of Big O notation in describing these growth rates.
🔍 Analyzing Growth Rates and the Dominance of Terms
This paragraph delves deeper into the comparison of growth rates by examining the behavior of functions as they approach both zero and infinity. The professor uses the example of a polynomial function to demonstrate how lower-order terms dominate as the variable approaches zero, while higher-order terms become significant as the variable approaches infinity. The importance of understanding the direction of the limit is highlighted to avoid confusion. The concept of Big O notation is formally introduced with a clear definition and its two forms, one for functions approaching infinity and the other for functions approaching zero. The paragraph also explains how Big O notation can be applied to various mathematical expansions, such as the Taylor series for arctan(x), to provide an upper bound on the growth of functions.
📈 Examples and Properties of Big O Notation
The third paragraph provides a series of examples to illustrate the application of Big O notation to different mathematical functions, both as they approach zero and infinity. It discusses how certain functions fall within the Big O category for specific powers of the variable, while others do not. The properties of Big O notation are explored, such as the rules for multiplication and addition of functions within this notation. The paragraph also uses the binomial series to provide more precise bounds on the growth of functions and emphasizes the importance of these rules in understanding the behavior of functions in the context of asymptotic analysis.
🌐 Conclusion and Transition to Derivatives
In the concluding paragraph, the professor summarizes the key points of the lecture on asymptotics, emphasizing the importance of understanding growth rates and the utility of Big O notation in describing these rates. The lecture concludes with a segue into the next chapter, which will focus on the concept of derivatives. The connection between the rates of change discussed in the lecture and the formal definition of derivatives is highlighted, indicating that the knowledge gained from the study of asymptotics will be foundational for understanding the derivative as a measure of instantaneous rate of change.
Mindmap
Keywords
💡Asymptotics
💡Big O Notation
💡L'Hôpital's Rule
💡Monomial
💡Exponential Function
💡Polynomial Function
💡Logarithmic Function
💡Factorial Growth
💡Order of Growth
💡Taylor Series
💡Limit
Highlights
Introduction to Lecture 9 on orders of growth and asymptotics, focusing on how functions behave when they become very small or large.
Explanation of how different functions, such as monomials and exponential functions, grow at different rates as X approaches infinity.
Use of L'Hôpital's rule to compare the growth rates of functions, illustrating that exponential functions grow faster than polynomials.
Demonstration that linear growth is faster than logarithmic growth, even when the logarithmic function is raised to a power.
Introduction of the concept of Big O notation as a language to describe the upper bounds of growth rates of functions.
Description of the hierarchy of functional growth as X approaches infinity, from constant functions to exponential growth.
Discussion on factorial growth, which is faster than exponential growth, as an example of growth beyond exponential.
Analysis of the behavior of monomials X^N for N > 0 as X approaches both infinity and zero, highlighting the duality in growth rates.
Example of calculating limits for a polynomial expression as X approaches zero and infinity, showing the dominance of lower and higher order terms respectively.
Emphasis on the importance of the direction of the limit (X approaching 0 or infinity) in understanding the growth or shrinkage of functions.
Definition of a function f being in Big O of X^N, with an explanation of the upper bound it implies for the growth of f.
Examples of functions and their Big O classifications, such as arctan(X) being Big O of X^3 and e^(-1/X^2) being Big O of any positive power of X.
Explanation of the rules of Big O notation, including the effects of multiplication and addition of functions on their Big O classifications.
Application of Big O rules to simplify expressions involving exponential and polynomial functions as X approaches zero.
Transition from the first chapter to the second, where the concepts of rates of change will be formalized into the notion of a derivative.
Overall, the lecture provides a comprehensive introduction to the concepts of growth rates, asymptotic behavior, and Big O notation in the context of calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: