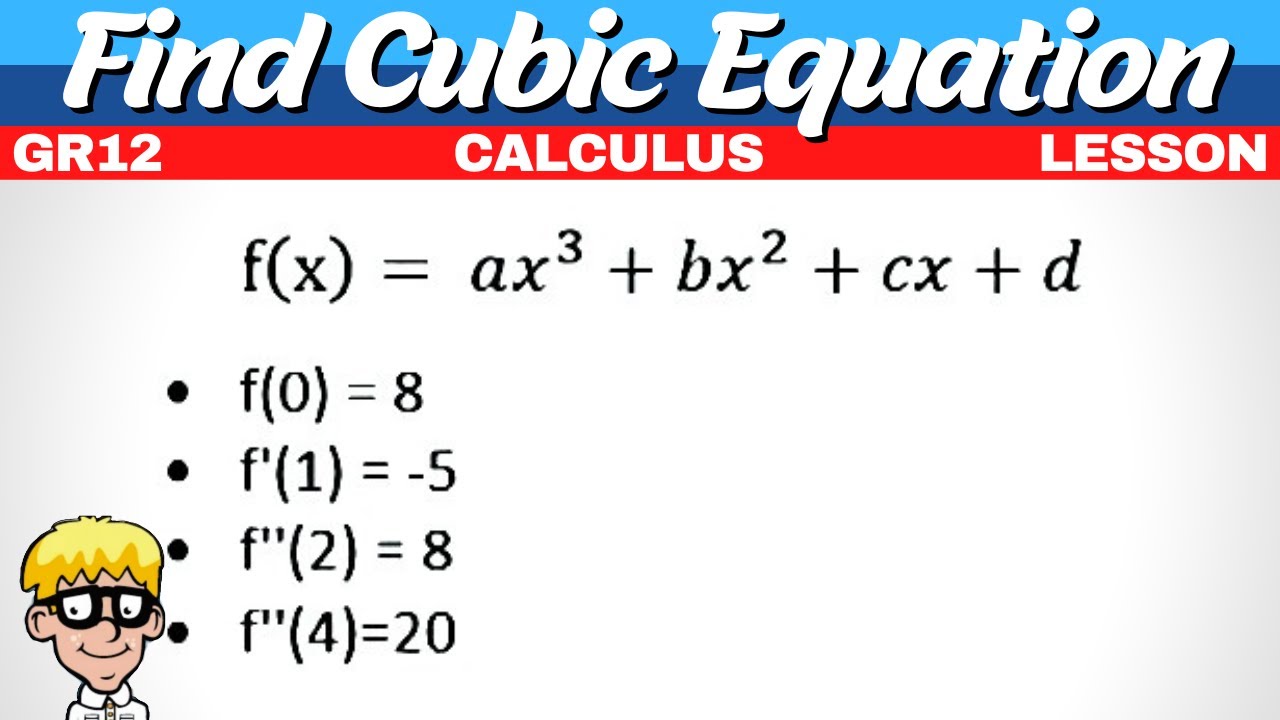Determine Cubic Equation grade 12
TLDRIn this educational video, the instructor guides viewers through solving a calculus problem involving finding the equation of a quadratic function. They emphasize the importance of using given x-intercepts and derivatives to simplify the process. The method involves plugging in values to form equations, reducing the number of variables, and solving simultaneous equations to find the coefficients a, b, c, and d. The instructor demonstrates a step-by-step approach, highlighting the ease of obtaining the solution and encouraging viewers to master the technique for easy marks.
Takeaways
- 😀 The video is about solving a mathematical problem involving finding the equation of a function given certain conditions.
- 😄 It emphasizes that the problem is easy and the conditions provided are helpful for finding the solution.
- 😁 The video mentions x-intercepts but notes that the problem at hand involves the first and second derivatives instead.
- 😉 The first condition given is that when x is zero, y is minus four, which helps find the value of 'd' in the equation.
- 😊 The first derivative of the function is derived and used to find a relationship between coefficients 'a', 'b', and 'c'.
- 😌 When x is two, the first derivative equals -26, leading to an equation involving 'a' and 'b'.
- 😆 The second derivative is discussed, and it's noted that as derivatives are taken, the number of variables decreases, which is beneficial.
- 😎 The value of the second derivative when x is one is used to create another equation involving 'a' and 'b'.
- 😏 The video demonstrates how to combine the equations to solve for the variables 'a' and 'b' using simultaneous equations.
- 😇 It's shown that 'a' can be isolated and solved for, finding that 'a' equals one.
- 🙂 Once 'a' is known, it's used to find the value of 'b', which turns out to be negative eight.
- 😉 With 'a' and 'b' determined, the video shows how to find 'c' using the previously derived equations.
- 😃 Finally, the complete function is expressed with the found coefficients and the constant 'd'.
Q & A
What is the significance of finding the x-intercepts in a problem?
-Finding the x-intercepts is significant because it simplifies the process of determining the equation of a curve. If the x-intercepts are given, it's easier to establish the form of the equation by substituting these points directly into the equation.
Why is it beneficial to have fewer variables in an equation when solving for derivatives?
-Having fewer variables in an equation makes it easier to solve, as it reduces the complexity of the system. It allows for a more straightforward application of algebraic methods to find the values of the remaining variables.
What is the purpose of the first derivative in the context of the given script?
-The first derivative is used to find the slope of the curve at any given point. In the script, it is used to establish a relationship between the coefficients of the equation when a specific x-value is given.
How does the second derivative relate to the problem discussed in the script?
-The second derivative provides information about the concavity of the curve and is used to find the points where the curve changes direction. In the script, it helps to further constrain the values of the coefficients by providing another equation when a specific x-value is given.
What does the script suggest about the process of solving for the coefficients of a polynomial given its derivatives?
-The script suggests a methodical approach where information from the first and second derivatives at specific points is used to create a system of equations. This system can then be solved to find the unknown coefficients of the polynomial.
Why is it important to plug the given information into the equations derived from the derivatives?
-Plugging the given information into the equations is crucial because it allows you to create a system of equations that can be solved for the unknown variables. This step is essential for finding the specific form of the polynomial.
What is the role of the value 'd' in the script, and how is it found?
-In the script, 'd' represents the y-intercept of the polynomial. It is found by using the given information that when x is zero, y is minus four, which directly gives the value of 'd' as -4.
How does the script handle the situation where the x-intercepts are not given?
-When the x-intercepts are not given, the script uses the information related to the first and second derivatives at specific x-values to set up a system of equations. This system is then solved for the coefficients of the polynomial instead.
What is the strategy for solving simultaneous equations in the context of the script?
-The strategy involves isolating one variable in one equation and then substituting this value into the other equation to find the second variable. This process is repeated until all variables are determined.
How does the script ensure that the solution for the coefficients is correct?
-The script ensures the correctness of the solution by using the derived equations from the given information about the derivatives and the curve's behavior at specific points. Once all coefficients are found, they can be substituted back into the original equations to verify the solution.
What is the final form of the polynomial found in the script?
-The final form of the polynomial, as derived from the script, is f(x) = x - 8x^2 - 6x - 4, with the coefficients a, b, c, and d found to be 1, -8, -6, and -4, respectively.
Outlines
😀 Introduction to Solving Equations with Given Derivatives
The speaker begins by encouraging a positive attitude towards a math problem involving finding an equation of a curve given certain conditions. They explain that even though the problem may seem lengthy, it is straightforward and worth the effort. The focus is on using given x-intercepts and derivatives to find the equation of the curve. The speaker emphasizes that when x-intercepts are provided, the problem becomes simpler, but in this case, the information given relates to the first and second derivatives, requiring a different approach.
📚 Utilizing Given Points and Derivatives to Find Coefficients
The speaker proceeds to guide through the process of using the given points and derivatives to find the coefficients of the equation. They start by identifying a point where x=0 and y=-4, which helps in determining the value of 'd'. Next, they move on to find the first derivative and use the information that at x=2, the derivative equals -26. This leads to an equation involving 'a', 'b', and 'c', which cannot be solved immediately but is noted for further use. The speaker also introduces the second derivative and its role in simplifying the equation by reducing the number of variables.
🔍 Solving for Variables Using Simultaneous Equations
The speaker continues by focusing on the second derivative and the given y-value when x=1, which is -10. They form an equation involving 'a' and 'b' and then cleverly use the information to isolate 'b' in terms of 'a'. The speaker demonstrates the process of substituting this expression for 'b' into another equation to solve for 'a'. They find that 'a' equals 1 and then use this value to find 'b', which turns out to be -8. This step-by-step method of solving simultaneous equations is highlighted as a key strategy for finding the unknowns.
🎯 Finalizing the Equation with Found Coefficients
With 'a' and 'b' determined, the speaker concludes the process by using these values to find 'c' from one of the earlier equations. They substitute the values of 'a' and 'b' into the equation involving the first derivative at x=2, which yields the value of 'c' as -6. The speaker then presents the final equation of the curve as f(x) = x^3 - 8x^2 - 6x - 4, summarizing the entire process and emphasizing the satisfaction of arriving at the correct solution through systematic problem-solving.
Mindmap
Keywords
💡x-intercepts
💡first derivative
💡second derivative
💡simultaneous equations
💡variable
💡function
💡slope
💡concavity
💡tangent line
💡coefficients
💡equation
Highlights
Finding the equation of a quadratic function using given information about x-intercepts, first and second derivatives.
If x-intercepts are given, it's easy to find the equation by filling in the values.
When x-intercepts are not given, use information about the first and second derivatives instead.
Plug in the given point (0, -4) to find the value of d.
The first derivative is 3ax^2 + 2bx + c, with d falling away.
Use the given first derivative value at x=2 to create an equation with a, b, and c.
The second derivative simplifies to 6ax + 2b as you take more derivatives.
Plug in the y value at x=1 to create another equation with a and b.
Combine the two equations with two unknowns (a and b) to solve them simultaneously.
Isolate b in one equation and substitute it into the other to solve for a.
Once a is found, substitute it back to find the value of b.
With a and b known, find c using another equation.
The final equation is f(x) = ax^2 + bx + c + d, with all coefficients found.
Emphasizes the importance of careful work to avoid simple mistakes like misplaced signs.
Highlights the method of solving for coefficients in a quadratic function given derivative information.
Encourages learners to not only follow the presented method but also explore other ways to solve simultaneous equations.
Provides a step-by-step guide on how to approach the problem methodically.
Stresses the value of reducing the number of variables in equations to simplify solving.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: