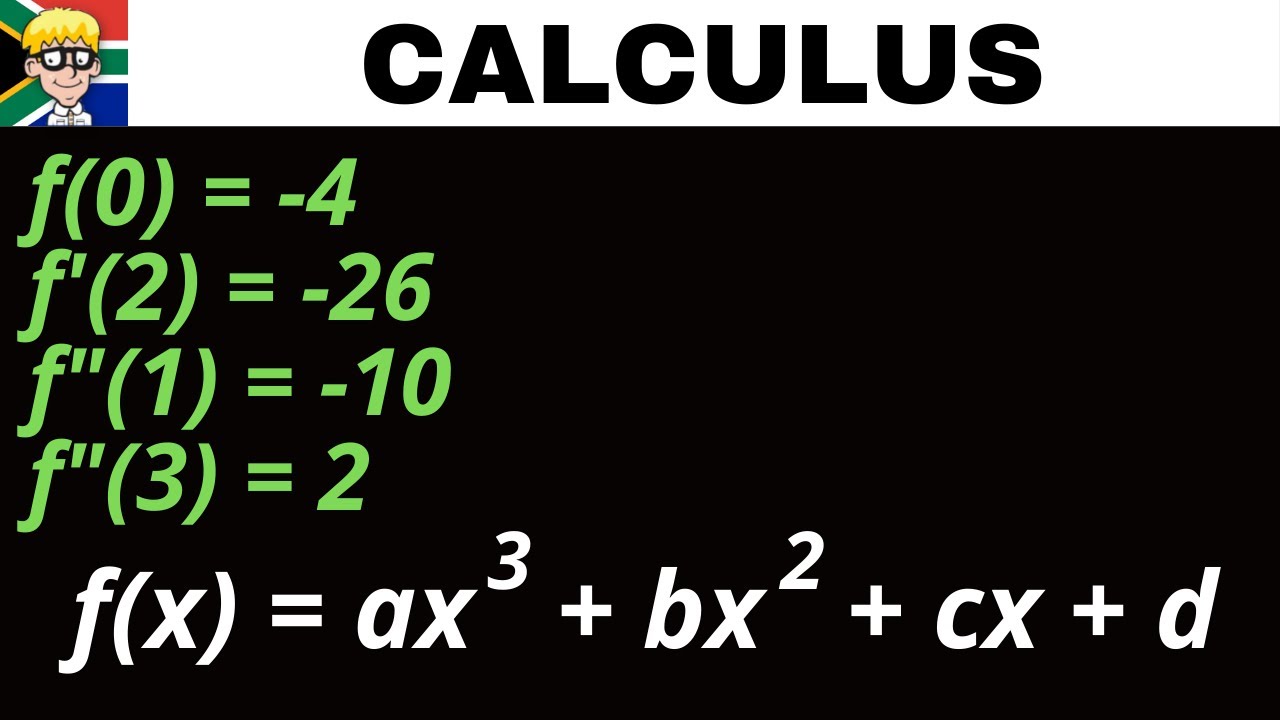Determine Cubic Equation Calculus grade 12

Kevinmathscience

18 Sept 202004:28

EducationalLearning

32 Likes 10 Comments

TLDRThis lesson teaches the method of determining the equation of a cubic graph using given information. The instructor demonstrates the process by substituting values into the cubic equation and its derivatives to solve for the coefficients. The steps include finding the value of 'd' by setting x to zero, deriving the first and second derivatives, and using additional points to establish equations for 'a' and 'b'. Through solving simultaneous equations, the values of 'a' and 'b' are determined, and subsequently, 'c' is found. The final cubic function is constructed, emphasizing the importance of systematic substitution and solving.

Takeaways

📚 The lesson focuses on determining the equation of a cubic graph using given information.
🔍 To find the equation, plug the provided values into the appropriate mathematical equations step by step.
📝 Start by substituting x = 0 into the cubic function to find the value of 'd', which is 8 in the given example.
📈 Derive the first derivative of the cubic function to find the slope at a specific point, in this case, when x = 1, resulting in an equation with 'a' and 'b'.
📉 Take the second derivative to further analyze the function's concavity and find another equation involving 'a' and 'b' when x = 2.
🔢 Use the second derivative again with x = 4 to create a third equation that will help solve for 'a' and 'b'.
🔑 Solve the system of equations derived from the second and third derivatives to find the values of 'a' and 'b'.
🔄 Substitute the found values of 'a' and 'b' back into the first derivative equation to solve for 'c'.
📐 With all coefficients determined, construct the complete cubic function equation.
📝 Remember to include the constant term 'd' in the final equation, which was found to be 8.
🔎 The most crucial part of the process is accurately plugging in the values and solving the resulting equations.

Q & A

What is the main topic of the lesson?
-The main topic of the lesson is determining the equation of a cubic graph using given information and plugging it into the appropriate equations.
What is the first step in finding the equation of the cubic graph?
-The first step is to plug in the x value of zero into the function f to find the value of d, which is given to be 8 in this case.
How is the first derivative of a cubic function represented?
-The first derivative of a cubic function is represented as 3ax^2 + 2bx + c, where a, b, and c are coefficients to be determined.
What is the purpose of plugging the x value of 1 into the first derivative?
-The purpose is to find a relationship between the coefficients a and b, as the derivative at x=1 is given to be -5, which helps in forming an equation to solve for these coefficients.
What does the second derivative represent in the context of this lesson?
-The second derivative, represented as 6ax + 2b, is used to find additional relationships between the coefficients a and b by plugging in different x values.
How many equations are formed by plugging in x values of 2 and 4 into the second derivative?
-Two equations are formed: one from x=2, which gives 12a + 2b = 8, and another from x=4, which gives 24a + 2b = 20.
What method is used to solve for the coefficients a and b?
-Simultaneous equations are used to solve for the coefficients a and b by substituting one equation into the other and simplifying.
What is the value of a found using the simultaneous equations?
-The value of a is found to be 1 by solving the simultaneous equations.
What is the value of b after substituting the value of a?
-After substituting a = 1, the value of b is found to be -2.
How is the value of c determined in the equation?
-The value of c is determined by plugging in the found values of a and b into the equation derived from the first derivative at x=1, which results in c = -4.
What is the final cubic function equation found in the lesson?
-The final cubic function equation is f(x) = x^3 - 2x^2 - 4x + 8.

Outlines

00:00

📊 Understanding the Cubic Graph Equation

This paragraph introduces the process of working out the equation of a cubic graph. It emphasizes the importance of using provided information and correctly plugging it into the appropriate equation. The example given involves determining the equation of a graph by systematically using given x-values and their corresponding outputs.

🔢 Solving for the Constant 'd'

The second part explains how to find the constant 'd' by substituting x = 0 into the cubic equation. This step is demonstrated by showing that when x = 0, the equation simplifies, allowing for the determination of d, which is found to be 8. This is the first step in solving for the constants of the cubic equation.

📈 First Derivative and Plugging in Values

Here, the focus shifts to the first derivative of the cubic function. The paragraph describes how to obtain the first derivative and how to use a given x-value of 1 to find one of the constants in the equation. The process of plugging in the x-value and simplifying the equation to obtain useful information is emphasized.

🧮 Second Derivative for Further Solutions

This paragraph details the use of the second derivative to further solve the cubic equation. By plugging in x = 2 into the second derivative, the equation is simplified to provide another relationship between the constants 'a' and 'b'. This step is crucial for gathering additional equations needed to solve the system.

📝 Simultaneous Equations for 'a' and 'b'

In this section, the method of solving the system of simultaneous equations is explained. Two equations with two unknowns, 'a' and 'b', are solved by substitution. The process involves rearranging one equation and substituting it into the other to find the values of 'a' and 'b'.

🔄 Final Steps: Solving for 'c' and Forming the Equation

The final paragraph concludes the process by solving for 'c' using the previously found values of 'a' and 'b'. After finding 'c', the complete cubic equation is formed, summarizing the entire process of determining the cubic function. The paragraph reinforces the importance of methodically using the given information to solve for all constants.

Mindmap

Keywords

💡Cubic Graph

A cubic graph refers to a mathematical graph that represents a cubic function, which is a polynomial of degree three. In the video, the cubic graph is the subject of the lesson, where the process of determining the equation of such a graph is explained using given information and algebraic manipulation.

💡Equation

An equation is a statement that asserts the equality of two expressions, typically involving variables. In the context of the video, the equation refers to the specific form of a cubic function that the instructor is guiding the viewer to derive using provided data points and derivatives.

💡Derivative

The derivative of a function is a measure of the rate at which the function's value changes with respect to its variable. In the video, the first and second derivatives of the cubic function are calculated to find specific coefficients (a, b, and c) that define the cubic equation.

💡First Derivative

The first derivative of a function is the initial step in finding the rate of change or slope of the function at any given point. In the script, the first derivative is used to find the value of the function's slope when x is 1, which helps in determining the coefficients of the cubic equation.

💡Second Derivative

The second derivative provides information about the concavity of a function and the rate of change of the first derivative. In the video, the second derivative is used to find the values of the coefficients a and b by plugging in specific x values and solving the resulting equations.

💡Coefficients

In algebra, coefficients are numerical factors in a term of a polynomial. In the context of the video, the coefficients a, b, and c are the unknowns that need to be determined to find the complete equation of the cubic graph.

💡Simultaneous Equations

Simultaneous equations are a set of equations that are solved together to find a common solution for the variables they contain. In the video, the instructor uses two equations with two unknowns (a and b) to solve for these coefficients using the method of substitution or elimination.

💡Plugging In

To 'plug in' refers to the process of substituting specific values into an equation or expression to find an unknown. Throughout the video, the instructor repeatedly plugs in different x values into the derivatives to derive the necessary coefficients for the cubic equation.

💡Solving

Solving in mathematics involves finding the values of variables that make an equation true. In the video, the process of solving involves using the information obtained from plugging in values into the derivatives to find the specific coefficients of the cubic equation.

💡Algebraic Manipulation

Algebraic manipulation refers to the process of transforming equations or expressions using algebraic rules to simplify or solve them. In the video, the instructor uses algebraic manipulation to rearrange and combine equations to isolate and solve for the coefficients of the cubic function.

💡Contextualization

Contextualization in the video refers to the specific application of mathematical concepts to the problem at hand. The instructor contextualizes the process of finding the cubic equation by applying the given information to the correct algebraic forms and solving for the unknowns.

Highlights

Lesson focuses on finding the equation of a cubic graph using given information.

Plugging in x=0 gives f(0)=8, allowing us to find that d=8.

Finding the first derivative f'(x)=3ax^2+2bx+c helps in further calculations.

Plugging x=1 into f'(x) and setting it to -5 gives an equation for a and b.

Calculating the second derivative f''(x)=6ax+2b is key for finding a and b.

Setting f''(2)=8 provides an equation involving a and b.

Simplifying equations by dividing helps in solving for a and b.

Using the second derivative at x=4 gives another equation to solve for a and b.

Solving the system of equations for a and b using simultaneous equations.

Rearranging equation B to isolate b and substituting into equation A.

Solving for a gives a=1 by comparing coefficients.

Substituting a=1 into the equation to find b=-2.

Using found values of a and b to solve for c from the original equation.

Determining c=-4 by simplifying the equation.

Final cubic equation is f(x)=x^3-2x^2-4x+8.

Emphasizing the importance of plugging values into the appropriate equations and solving.

Transcripts

Browse More Related Video

Determine Cubic Equation grade 12

Draw Cubic Graph Grade 12

Determine Cubic Equation grade 12

7.1.1 Solving a System of Equations Using Substitution

Draw Cubic Graph Grade 12

Calculus Grade 12: Practice