Definite integral as the limit of a Riemann sum | AP Calculus AB | Khan Academy
TLDRThe video script discusses the concept of approximating the area under a curve using rectangles, a method known as Riemann sums. It explains how equal partitions of the interval and the function's value at specific points determine the height of the rectangles. The script further clarifies that Riemann sums can take various forms, such as using trapezoids or non-equal partitions, and emphasizes that the Riemann integral is a rigorous definition of an integral, obtained by taking the limit of Riemann sums as the number of partitions approaches infinity.
Takeaways
- 📈 The concept of approximating the area under a curve using rectangles is introduced as a fundamental technique in calculus.
- 📊 The method of equal partitioning of the interval between two boundaries (a and b) and using the function's value at the left endpoint to determine the height of rectangles is explained.
- 🧩 The generalization of this approach into sigma notation is discussed, highlighting the summation of areas of rectangles as an approximation of the actual area under the curve.
- 🔄 The possibility of varying the height of the rectangles based on the function's value at the right endpoint or midpoint is mentioned, expanding on the initial example.
- 🏗️ The construction of trapezoids as an alternative to rectangles for a more accurate approximation is introduced, emphasizing the flexibility of Riemann sums.
- 🌐 Riemann sums are defined as a broader concept, not limited to the specific methods discussed, and can involve non-equal partitions as well.
- 👨💼 Bernhard Riemann, after whom Riemann sums are named, is recognized for his significant contributions to mathematics, particularly the Riemann integral.
- 🔢 The Riemann integral is presented as a rigorous and mainstream formal definition of an integral, building upon the ideas of Newton and Leibniz.
- 💭 The limit of a Riemann sum as the number of partitions (n) approaches infinity is described as the way to define the definite integral.
- 📊 The visual representation of the limit process is provided, illustrating how infinitesimally small rectangles (dx) approximate the actual area under the curve.
- 🔍 The notion of 'dx' as an infinitely small change is explored, connecting the concept to the width of the rectangles and the summation process.
Q & A
What is the main concept discussed in the video?
-The main concept discussed in the video is the Riemann sum, a method for approximating the area under a curve by breaking it into rectangles and summing their areas.
How does the Riemann sum relate to the concept of a definite integral?
-The Riemann sum is used to approximate the area under a curve, and as the number of rectangles (partitions) increases and the width of each rectangle (Δx) approaches zero, the Riemann sum converges to the exact value of the definite integral.
What are the different types of Riemann sums mentioned in the video?
-The video mentions left Riemann sum, right Riemann sum, and midpoint Riemann sum, as well as the use of trapezoids for approximation.
How does the left Riemann sum approximate the area under a curve?
-The left Riemann sum approximates the area by using the left endpoint of each partition to determine the height of the rectangles, summing these areas to estimate the total area under the curve.
How does the right Riemann sum differ from the left Riemann sum?
-The right Riemann sum differs from the left Riemann sum by using the right endpoint of each partition to determine the height of the rectangles, instead of the left endpoint.
What is the significance of Bernhard Riemann in the context of this video?
-Bernhard Riemann is the mathematician after whom Riemann sums and Riemann integrals are named. He is known for his contributions to mathematics, particularly the rigorous definition of the integral in calculus.
What happens when the number of partitions (n) in a Riemann sum increases?
-As the number of partitions (n) increases, the width of each rectangle (Δx) decreases, leading to a more accurate approximation of the area under the curve. In the limit as n approaches infinity, the Riemann sum converges to the exact value of the definite integral.
How is the concept of dx related to the Riemann sum?
-The concept of dx can be thought of as an infinitely small change in x (but not zero), which is related to the width of the rectangles (Δx) in the Riemann sum. The integral is represented as the sum of the product of the function value and an infinitesimally small change in x (dx) over the interval from a to b.
What is the connection between the width of the rectangles (Δx) and the differential (dx)?
-The width of the rectangles (Δx) can be conceptualized as approaching the differential (dx) as it becomes infinitely small. This connection helps in understanding the transition from Riemann sums to the integral as a limit process.
How does the video script relate to the historical development of calculus?
-The video script relates to the historical development of calculus by mentioning that while Newton and Leibniz formulated the idea of the integral, it was the Riemann integral that provided a more formal and rigorous definition of what an integral is.
What is the purpose of discussing the Riemann sum in the context of calculus?
-Discussing the Riemann sum in calculus helps in understanding the concept of integration and provides a foundation for the Riemann integral, which is a fundamental tool for solving a wide range of mathematical problems.
Outlines
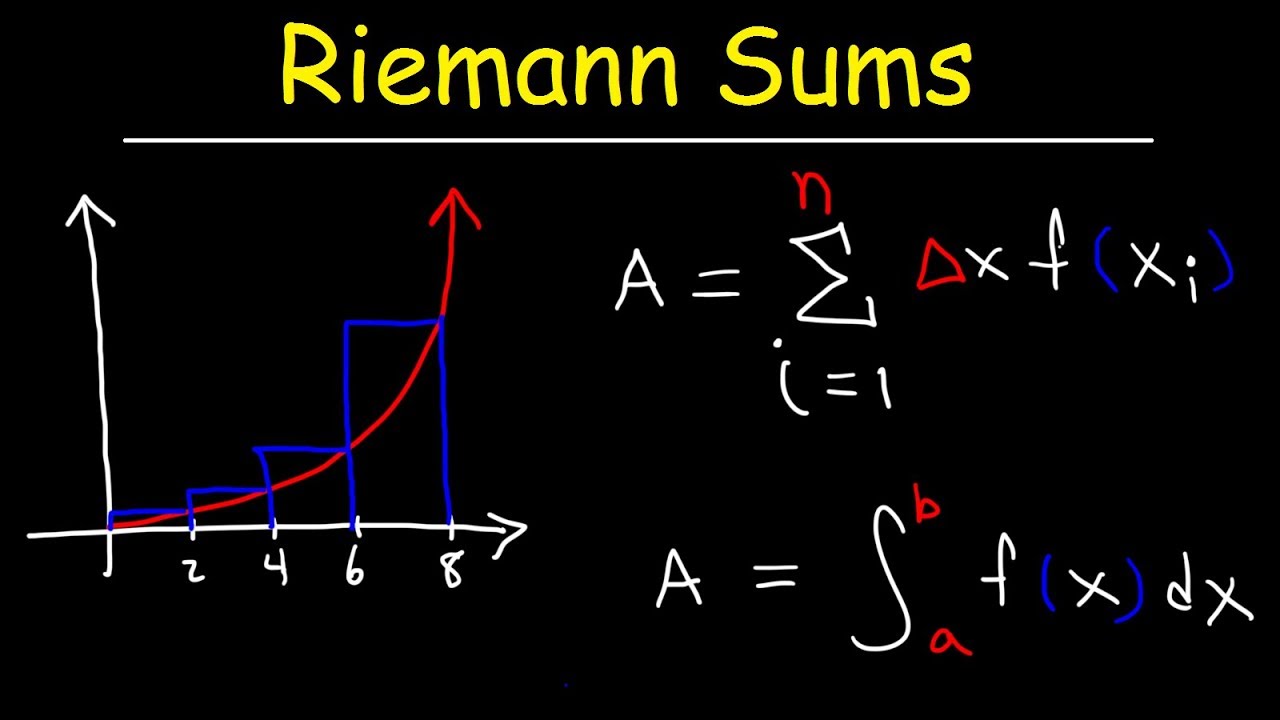
📊 Introduction to Riemann Sums and Approximating Areas Under Curves
The paragraph introduces the concept of approximating the area under a curve using Riemann sums. It explains the method of dividing the area into rectangles with equal width, using the function value at the left endpoint to determine the height of the rectangles. The idea of generalizing this process with sigma notation is also mentioned. The paragraph further discusses variations of Riemann sums, such as using right endpoints or midpoints for determining the height and constructing trapezoids. The concept of Riemann sums is related to the work of Bernhard Riemann, and it is highlighted that these sums form the basis for the Riemann integral, which is a formal definition of an integral in calculus. The integral is defined as the limit of Riemann sums as the number of rectangles approaches infinity, symbolized by the integral from a to b of f(x) dx. The paragraph concludes by noting that while the definition of the integral has been introduced, the actual evaluation of it will be covered in future videos.
Mindmap
Keywords
💡Approximating Area
💡Riemann Sums
💡Equally-Partitioned Intervals
💡Sigma Notation
💡Trapezoids
💡Definite Integral
💡Limit
💡Bernhard Riemann
💡Newton and Leibniz
💡Differential (dx)
💡Left Riemann Sum
Highlights
The video discusses approximating the area under a curve using rectangles.
The method involves breaking the area into rectangles and summing their areas as an approximation.
The rectangles have equal width, and the interval between boundaries a and b is equally partitioned.
The height of the rectangle is determined by the function evaluated at the left endpoint.
The concept was generalized and expressed in sigma notation.
Different methods of defining the height of rectangles were explored, such as right endpoint or midpoint.
Trapezoids were constructed as a particular instance of Riemann sums.
Riemann sums are named after Bernhard Riemann, a prominent mathematician.
Riemann is most known for the Riemann sum and the Riemann integral in first-year calculus courses.
The Riemann integral is a rigorous definition of an integral, different from the ideas of Newton and Leibniz.
The integral is defined as the limit of Riemann sums as n approaches infinity.
As n approaches infinity, the rectangles become infinite in number and better approximate the actual area.
The actual area under the curve is denoted by the integral from a to b of f(x)dx.
The concept of dx as an infinitely small change is introduced.
The differential dx can be thought of as an infinitely small but non-zero change.
The video explains that the integral is the sum of an infinite number of function times differential dx from a to b.
Different types of Riemann sums are mentioned, such as left Riemann sum, right Riemann sum, and using the midpoint.
The limit of any Riemann sum as n approaches infinity yields the Riemann definition of the integral.
The video is a part of a series, with further evaluation of Riemann sums to be discussed in future videos.
Transcripts
Browse More Related Video

BusCalc 13.4 Riemann Sums

Business Calculus - Math 1329 - Section 5.3 - The Definite Integral and Fundamental Thm of Calculus

Riemann Sums and Definite Integrals

Calculus 1: Definition of the Integral Examples

AP Calculus AB: Lesson 6.2 Riemann and Trapezoidal Sums
Riemann Sums - Left Endpoints and Right Endpoints
5.0 / 5 (0 votes)
Thanks for rating: