Proof: Volume ratios in a carnot cycle | Thermodynamics | Physics | Khan Academy
TLDRThe video script presents a mathematical proof of a fundamental thermodynamics concept: the ratio of volumes in a Carnot cycle at different states equates to the ratio of volumes at other states. Starting with the first law of thermodynamics and the definition of internal energy, the presenter uses calculus to integrate changes in temperature and volume during adiabatic processes. The proof concludes with a simple yet elegant result, demonstrating the relationship between volumes and temperatures in different states of the cycle.
Takeaways
- 📚 The video aims to prove a fundamental result in thermodynamics related to the ratio of volumes in a Carnot cycle.
- 🔍 The ratio of volume at state B to state A is equivalent to the ratio of volume at state C to state D in a Carnot cycle.
- 🧩 The proof involves understanding the concept of adiabatic processes, where there is no heat transfer (Q = 0).
- ⚙️ The first law of thermodynamics is central to the proof, stating that the change in internal energy (ΔU) equals the work done by the system minus the heat applied.
- 🔄 The internal energy (U) at any point in time is shown to be 3/2 times nRT, which is also equal to 3/2 times PV.
- 🌡️ A change in internal energy implies a change in temperature, as other factors like the number of molecules (n) and the universal gas constant (R) remain constant.
- 📉 The ideal gas law (PV = nRT) is used to express pressure in terms of temperature and volume, simplifying the equations for the proof.
- ∫ The proof involves integrating over infinitesimally small changes in volume (dV) and temperature (dT) during the adiabatic process.
- 📚 The antiderivative of 1/T is the natural logarithm of T, which is used to simplify the integral expressions.
- 🔗 The final result of the proof is that the ratio of final to initial temperatures and volumes for two adiabatic processes are equal, leading to the initial goal of showing VB/VA = VC/VD.
- 🎯 The proof concludes by demonstrating that the volume ratios in the Carnot cycle are consistent with the principles of adiabatic processes and the first law of thermodynamics.
Q & A
What is the main goal of the video?
-The main goal of the video is to prove that the ratio of the volume at state B to the volume at state A in a Carnot cycle is equal to the ratio of the volume at state C to the volume at state D.
What is an adiabatic process in thermodynamics?
-An adiabatic process is one where there is no transfer of heat into or out of the system, meaning the system is completely isolated from its surroundings.
How is the first law of thermodynamics applied in this video?
-The first law of thermodynamics is applied by stating that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system, which in an adiabatic process equals zero since no heat is transferred.
What is the relationship between internal energy and temperature in the context of this video?
-The internal energy at any point in time is related to the temperature by the formula 3/2 * n * R * T, where n is the number of molecules, R is the universal gas constant, and T is the temperature. A change in internal energy implies a change in temperature.
How is the ideal gas equation used in the video?
-The ideal gas equation, PV = nRT, is used to solve for the pressure P in terms of the other variables, which helps in the derivation of the relationship between changes in internal energy, pressure, and volume during an adiabatic process.
What is the significance of integrating over small changes in temperature and volume?
-Integrating over small changes in temperature and volume allows the calculation of the total work done by the system during an adiabatic process, which is crucial for proving the main result of the video.
What mathematical property is used to simplify the equation involving changes in internal energy and volume?
-The property of logarithms is used to simplify the equation, allowing the separation of variables and making it possible to integrate over changes in temperature and volume.
What is the final result derived from the integration process in the video?
-The final result derived is that the ratio of the final temperature to the initial temperature raised to the power of 3/2, multiplied by the ratio of the final volume to the initial volume, equals 1 for an adiabatic process.
How does the video relate the derived result to the specific volumes and temperatures in the Carnot cycle?
-The video applies the derived result to the specific adiabatic processes in the Carnot cycle, showing that the ratio of volumes and temperatures for the process from B to C is equal to the ratio for the process from D to A.
What is the final equation that the video proves?
-The final equation proved in the video is that the ratio of volume B to volume A (VB/VA) is equal to the ratio of volume C to volume D (VC/VD).
Outlines
🔍 Introduction to Proving a Thermodynamic Ratio
The video begins with an introduction to the goal of proving a simple thermodynamic result: the ratio of volumes in a Carnot cycle. The presenter emphasizes that this is a straightforward result, suggesting that viewers familiar with the concept may not need to watch the entire video. However, for those interested in the mathematical journey, the video promises to explore adiabatic processes in more depth. The key steps in the proof revolve around the adiabatic process from state D to A, where no heat is transferred, and the first law of thermodynamics is applied to establish a foundational equation relating internal energy change, pressure, and volume change.
📚 Derivation of the Adiabatic Process Equation
This paragraph delves into the mathematical derivation for the adiabatic process. The presenter uses the first law of thermodynamics and the ideal gas law to establish an equation that relates changes in internal energy, pressure, and volume. By setting the heat transfer to zero for an adiabatic process, an equation is derived that equates the change in internal energy plus the work done by the system to zero. The internal energy is then expressed in terms of temperature and volume, leading to an integral equation that will be used to analyze the adiabatic process in detail.
🧩 Integrating Over Adiabatic Changes
The presenter continues by discussing the integration over small changes in temperature and volume during the adiabatic process. By dividing the derived equation by nRT and simplifying, an integral equation is formed that relates the natural logarithms of temperature and volume changes. The antiderivative of the equation is taken, leading to an expression that equates the natural logarithm of the ratio of final to initial temperatures and volumes. This is set to zero, indicating that the sum of all infinitesimal changes in the adiabatic process equals zero.
🎯 Conclusion of the Thermodynamic Proof
The final paragraph concludes the proof by applying the results of the adiabatic process to the specific volumes and temperatures of the Carnot cycle. The presenter demonstrates that the ratio of final to initial temperatures and volumes for two different adiabatic processes are equal to one another, leading to the conclusion that the ratio of volumes VB to VC is equal to the ratio of VA to VD. This result is derived through a series of mathematical manipulations and applications of logarithmic properties, ultimately providing a clear and concise outcome that relates the volumes in the Carnot cycle.
Mindmap
Keywords
💡Carnot cycle
💡Adiabatic process
💡First law of thermodynamics
💡Internal energy
💡Ideal gas equation
💡Volume ratio
💡Temperature change
💡Kinetic energy
💡Logarithmic properties
💡Integral
Highlights
The video aims to prove a simple result about the ratio of volumes in a Carnot cycle.
The ratio of volume B to A is equal to the ratio of volume C to D in a Carnot cycle.
The proof involves adiabatic processes where there is no heat transfer.
Adiabatic processes are completely isolated from the rest of the world.
The first law of thermodynamics relates change in internal energy to heat and work done.
In an adiabatic process, the change in internal energy plus work done equals zero.
Internal energy at any point is equal to 3/2 times nRT, which is also 3/2 times PV.
Change in internal energy is related to change in temperature, as other factors are constant.
Using the ideal gas law PV = nRT to solve for pressure.
Substituting expressions for internal energy and pressure into the first law equation.
Dividing by nRT simplifies the equation to integrate over small changes in temperature and volume.
Integrating the simplified equation over the entire adiabatic process.
The antiderivative of 1/T is the natural log of T, and 1/V is the natural log of V.
The integrated equation relates the natural logs of final and initial temperatures and volumes.
The final equation derived is that the temperature ratio to the 3/2 power times the volume ratio equals 1.
Applying the derived equation to the two adiabatic processes in the Carnot cycle.
Setting the two equations equal to each other and simplifying leads to the desired result.
The final result is that the ratio of volume B to A is equal to the ratio of volume C to D.
The proof uses fundamental thermodynamic principles and mathematical integration.
Transcripts
Browse More Related Video

Carnot Engine

Entropy Change For Melting Ice, Heating Water, Mixtures & Carnot Cycle of Heat Engines - Physics
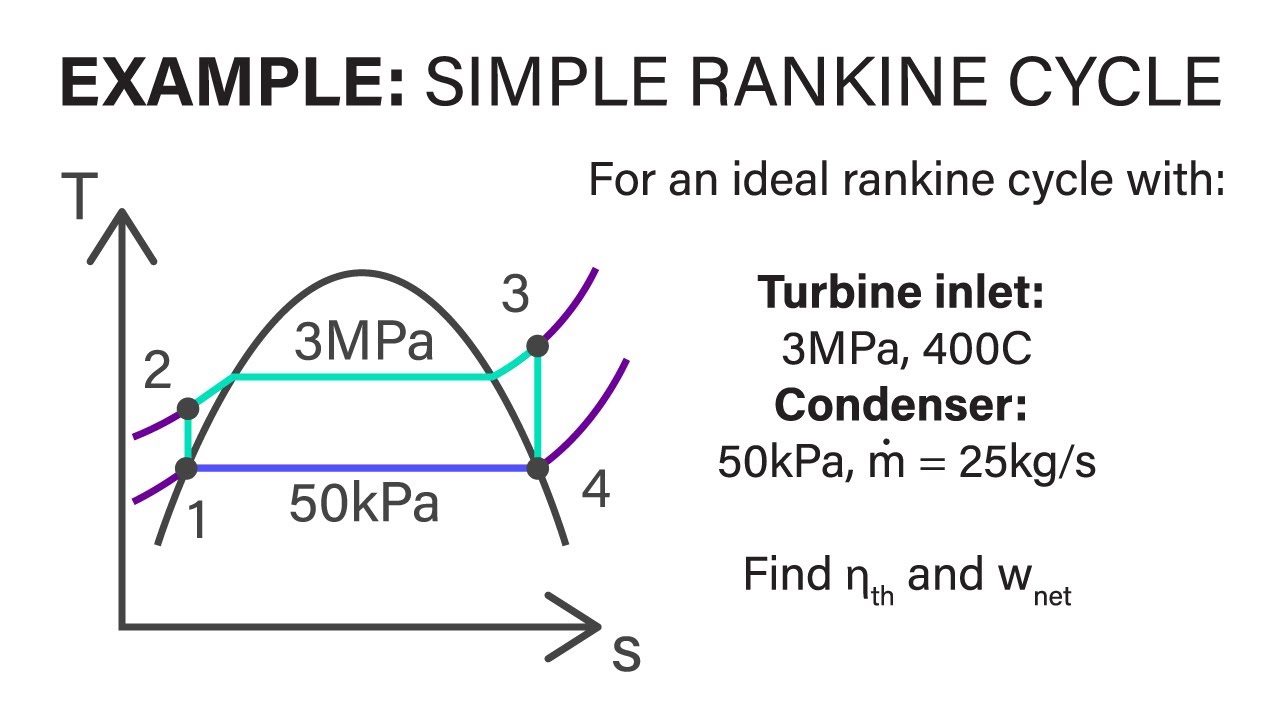
Mechanical Engineering Thermodynamics - Lec 21, pt 1 of 5: Example - Simple Rankine Cycle

Proof: S (or entropy) is a valid state variable | Thermodynamics | Physics | Khan Academy

23. The Second Law of Thermodynamics and Carnot's Engine
22. The Boltzmann Constant and First Law of Thermodynamics
5.0 / 5 (0 votes)
Thanks for rating: