Mechanical Engineering Thermodynamics - Lec 21, pt 1 of 5: Example - Simple Rankine Cycle

Ron Hugo
9 Oct 201314:43
EducationalLearning
32 Likes 10 Comments

TLDRThis lecture focuses on solving Rankine cycle problems, starting with a simple ideal cycle operating between 3 MPa boiler pressure and 50 kPa condenser pressure. The steam enters the turbine at 400°C, with a mass flow rate of 25 kg/s. The goal is to illustrate the cycle on a TS diagram, calculate the thermal efficiency, and determine the net power output in megawatts. The process involves using steam tables, reversible steady flow work equations, and the first law of thermodynamics to find unknown states and efficiency, revealing a 28.4% efficiency due to expansion into the two-phase region.

Takeaways
  • 📚 The lecture focuses on solving example problems involving the Rankine cycle, a thermodynamic cycle used in heat engines.
  • 🔍 The Rankine cycle in question is a simple ideal cycle with specified pressure limits and steam temperature at the turbine inlet.
  • 📈 The problem requires illustrating the cycle on a TS (Temperature-Entropy) diagram to understand the thermodynamic process.
  • 🔧 The thermal efficiency and net power output of the cycle are the main outcomes to be calculated from the problem.
  • 💧 The cycle starts with a compressed liquid state at the condenser pressure of 50 kPa and moves through the pump to the boiler pressure of 3 MPa.
  • 🌡️ The steam at the turbine inlet is superheated at 400 degrees Celsius, corresponding to the boiler pressure.
  • 🚀 The mass flow rate of the steam is given as 25 kg/s, which is crucial for calculating the power output.
  • ⚙️ The Rankine cycle involves a reversible steady flow work equation to determine the enthalpy changes in the pump and turbine.
  • 📊 The TS diagram is essential for identifying the states of the cycle, including the two-phase region where the efficiency may drop.
  • 🔥 The thermal efficiency is calculated using the first law of thermodynamics and the heat input to the boiler.
  • ⚡ The net power output is determined by multiplying the work per unit mass by the mass flow rate, resulting in megawatts.
  • 📉 The example problem demonstrates a Rankine cycle with an efficiency of 28.4%, which is affected by the expansion into the two-phase region.
Q & A

  • What is the Rankine cycle?

    -The Rankine cycle is an idealized thermodynamic cycle that converts heat into work, typically used in power plants to produce electricity. It consists of four stages: 1) pumping a liquid to a high pressure, 2) heating the liquid to a high temperature, 3) expansion through a turbine to generate work, and 4) condensing the fluid back to a liquid state.

  • What are the pressure limits of the Rankine cycle described in the script?

    -The Rankine cycle in the script operates between a boiler pressure of 3 MPa and a condenser pressure of 50 kPa.

  • What is the temperature and pressure at the inlet to the turbine?

    -The steam at the inlet to the turbine is at 400 degrees Celsius and corresponds to the boiler pressure of 3 MPa.

  • What is the mass flow rate of the cycle?

    -The mass flow rate of the cycle is given as 25 kilograms per second.

  • What is the purpose of showing the cycle on a TS diagram?

    -A TS (Temperature-Entropy) diagram is used to visualize the thermodynamic process of the cycle, helping to understand the changes in state variables and the work and heat transfer during each stage of the cycle.

  • What is the thermal efficiency of the cycle?

    -The thermal efficiency of the cycle is calculated to be 28.4%, which indicates the efficiency of converting heat into work.

  • What is the net power output of the cycle in megawatts?

    -The net power output of the cycle is calculated to be 20.51 megawatts.

  • Why is the specific volume important in the Rankine cycle?

    -The specific volume is important because it is used in the calculation of the work done by the pump, which is essential for determining the enthalpy changes in the cycle.

  • What does the script suggest about the expansion process in the turbine?

    -The script suggests that the expansion process in the turbine is assumed to be isentropic, meaning there is no entropy change during the expansion.

  • Why is it not ideal to expand into the two-phase region in a Rankine cycle?

    -Expanding into the two-phase region is not ideal because it can lead to the formation of droplets, which can cause a drop in efficiency due to the additional work required to vaporize the liquid droplets.

  • How is the enthalpy at state four determined?

    -The enthalpy at state four is determined using the known entropy at state three and the assumption of an isentropic expansion, which allows for the calculation of the state at 50 kPa in the two-phase region.

Outlines
00:00
🔍 Introduction to the Rankine Cycle Problem

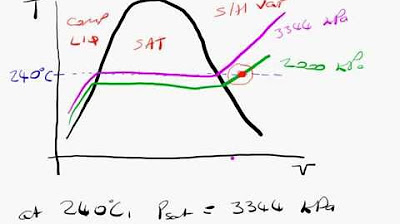
The script begins with an introduction to the Rankine cycle, outlining the task of solving example problems related to it. The focus is on a simple ideal Rankine cycle operating between specific pressure limits of 3 MPa and 50 kPa. The steam's temperature at the turbine inlet is given as 400°C, corresponding to the boiler pressure. The mass flow rate is 25 kg/s, and the goal is to illustrate the cycle on a TS diagram, calculate the thermal efficiency, and determine the net power output. The speaker emphasizes the importance of starting by noting down known information and sketching the TS diagram, which is a crucial step in understanding the problem's dynamics.

05:00
📚 Detailed Analysis of the Rankine Cycle States

This paragraph delves into the specifics of the Rankine cycle, starting with the known conditions at state one and moving through the pump to state two. The reversible steady flow work equation is used to calculate the enthalpy at state two, given the known pressure change and specific volume from the steam tables. The script then discusses the determination of whether the state is superheated by checking the conditions at 3 MPa and 400°C, leading to state three. The entropy is identified as a key parameter for calculating state four, assuming an isentropic expansion in the turbine. The script explains the process of linking states three and four using the constant entropy principle and finding the quality and enthalpy at state four, which completes the cycle's state analysis.

10:03
🔧 Calculation of Thermal Efficiency and Net Power Output

The final paragraph focuses on calculating the thermal efficiency and net power output of the Rankine cycle. The thermal efficiency is defined as the net work output divided by the heat input. The net work is calculated as the work out of the turbine minus the work into the pump, using the first law for steady flow devices. The heat input is determined from the enthalpy values on the TS diagram for the boiler process. By substituting the known values, the thermal efficiency is calculated to be 28.4%, which is considered not very high due to the expansion into the two-phase region. The net power output is then found by multiplying the mass flow rate with the work per unit mass, resulting in a power output of 20.51 MW. The script concludes by summarizing the problem-solving process and the importance of correctly drawing the TS diagram for accurate analysis.

Mindmap
Keywords
💡Rankine cycle
The Rankine cycle is a theoretical thermodynamic cycle that forms the basis for the operation of steam turbine systems used in power plants. In the context of the video, it represents the process by which the thermal energy is converted into work, which is then used to generate electricity. The script discusses solving problems related to this cycle, indicating its importance in understanding the efficiency and power output of the system.
💡Thermal efficiency
Thermal efficiency is a measure of how effectively heat energy is converted into work in a thermodynamic system. In the script, the concept is central to evaluating the performance of the Rankine cycle. The video explains how to calculate this efficiency by comparing the work output of the turbine to the heat input in the boiler, with the script revealing a thermal efficiency of 28.4% for the given example.
💡Net power output
Net power output refers to the usable power generated by a system after accounting for the power consumed by auxiliary equipment such as pumps. The script describes how to calculate this by multiplying the work per unit mass by the mass flow rate of the steam, resulting in a power output measurement in megawatts for the example problem.
💡Mass flow rate
Mass flow rate is the quantity of substance that passes a given point per unit of time. In the script, it is given as 25 kilograms per second and is a critical parameter in calculating the net power output of the Rankine cycle, as it determines the amount of steam that can be processed by the turbine.
💡Boiler pressure
Boiler pressure is the pressure at which steam is generated in a boiler, which is a key operating condition for the Rankine cycle. The script mentions a boiler pressure of 3 MPa, which is a high pressure that allows for efficient heat absorption and superheating of the steam.
💡Condenser pressure
Condenser pressure is the pressure at which steam is condensed back into water in the condenser, typically at a much lower pressure than the boiler to facilitate cooling. In the script, the condenser pressure is given as 50 kPa, which is significantly lower than the boiler pressure, indicating a pressure drop that drives the turbine.
💡Superheated steam
Superheated steam is steam that has been heated to a temperature above its saturation temperature, thus holding more energy than saturated steam at the same pressure. The script discusses the steam at the inlet to the turbine being at 400 degrees Celsius, which corresponds to being superheated at the boiler pressure of 3 MPa.
💡TS diagram
A TS diagram, or temperature-entropy diagram, is a graphical representation used in thermodynamics to illustrate the state changes of a system. The script emphasizes the importance of using a TS diagram to visualize the Rankine cycle, showing the process of heating, expansion, and cooling of the working fluid.
💡Isentropic process
An isentropic process is an idealized thermodynamic process in which the entropy of the system remains constant. In the script, the assumption of an isentropic expansion in the turbine allows for the determination of state four by equating the entropy at state three to that at state four, despite the unknowns in the system.
💡Two-phase region
The two-phase region refers to the area in a phase diagram where a substance can exist as a mixture of liquid and vapor. The script mentions that the expansion in the turbine leads to a state in the two-phase region, which is generally undesirable as it can lead to a drop in efficiency due to the formation of droplets.
Highlights

Introduction to solving example problems involving the Rankine cycle.

Explanation of the simple ideal Rankine cycle operating between boiler pressure at 3 MPa and condenser pressure of 50 kPa.

Description of steam conditions at the inlet to the turbine at 400 degrees Celsius and 3 MPa.

Presentation of the mass flow rate of 25 kilograms per second.

Objective to show the cycle on a TS diagram and calculate thermal efficiency and net power output.

Importance of beginning with known conditions when solving Rankine cycle problems.

Use of steam tables to find enthalpy and specific volume at state one (50 kPa).

Application of the reversible steady flow work equation to determine enthalpy at state two.

Identification of the superheated state at 3 MPa and 400 degrees Celsius for state three.

Utilization of entropy to link state three and four assuming an isentropic expansion process.

Determination of state four in the two-phase region using steam table values for SF and SG.

Calculation of the enthalpy at state four and the quality of the steam.

Application of the first law of thermodynamics to determine the thermal efficiency.

Calculation of the heat input in the boiler using enthalpy values.

Determination of the net work output and its relation to thermal efficiency.

Conclusion of the example problem with a thermal efficiency of 28.4% and a net power output of 20.51 MW.

Discussion on the implications of expanding into the two-phase region and its effect on efficiency.

Emphasis on the importance of correctly drawing the TS diagram for problem-solving.

Transcripts

Browse More Related Video

Engines: Crash Course Physics #24

Carnot Heat Engines, Efficiency, Refrigerators, Pumps, Entropy, Thermodynamics - Second Law, Physics

Steam tables: example 1

Carnot Engine

Carnot efficiency 2: Reversing the cycle | Thermodynamics | Physics | Khan Academy

Proof: Volume ratios in a carnot cycle | Thermodynamics | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Rankine CycleThermal EfficiencyTS DiagramSteam TablesSuperheatedTwo-Phase RegionPump WorkTurbine WorkNet Power OutputEngineering Problems