Work done by isothermic process | Thermodynamics | Physics | Khan Academy
TLDRThis educational video script explores the concept of isothermal processes in thermodynamics, using a container with a movable piston to illustrate the behavior of a gas under varying conditions. It explains how temperature, pressure, and volume are interrelated, and the role of a heat reservoir in maintaining constant temperature during expansion. The script delves into the mathematical representation of these processes, demonstrating how work done on the system and heat transfer are related, culminating in the formula for calculating work in an isothermal expansion.
Takeaways
- 📚 The classic system used for instruction involves a container with a movable piston and molecules creating pressure.
- ⚙️ The system starts with an initial pressure (P1), volume (V1), and temperature (T1), all in equilibrium.
- 🪨 Adding or removing rocks (pebbles) from the top of the piston helps approximate a quasi-static process, allowing the system to stay close to equilibrium.
- 🌡️ An isothermic process keeps the temperature constant throughout the process.
- 🛠️ Removing pebbles without external heat exchange (adiabatic process) would decrease the temperature as work is done by the system.
- ♻️ Placing the system on a reservoir maintains a constant temperature, creating an isothermic condition.
- 📈 On a PV (pressure-volume) diagram, an isothermic process traces a rectangular hyperbola, showing the relationship between pressure and volume at constant temperature.
- 🔢 The ideal gas law (PV = nRT) explains that at constant temperature, the product of pressure and volume is constant (PV = constant).
- 📉 Work done in an isothermic process is calculated as nRT times the natural log of the ratio of final to initial volume (W = nRT ln(V2/V1)).
- 🔥 In an isothermic process, the heat added to the system (Q) is equal to the work done by the system (Q = W), ensuring no change in internal energy.
Q & A
What is the significance of the movable piston in the container system described in the script?
-The movable piston represents a boundary that can change, allowing for variations in volume. It is crucial for demonstrating how changes in pressure, volume, and temperature affect the system during thermodynamic processes.
Why is the system described as being in equilibrium?
-The system is in equilibrium because all its properties, such as volume, pressure, and temperature, are uniform and consistent throughout. This uniformity is necessary to define macroscopic properties of the system.
What is an isothermic process, and how does it relate to the script's content?
-An isothermic process is a thermodynamic process in which the temperature of the system remains constant. The script discusses this process to explain how the system behaves when the temperature is maintained, even as other properties like volume change.
What does the term 'adiabatic' mean in the context of the script?
-Adiabatic refers to a process where there is no exchange of heat with the surroundings. The script uses this term to contrast with the isothermic process and to illustrate what happens when no external heat is added or removed from the system.
How does removing pebbles from the system affect its pressure and volume in an adiabatic process?
-In an adiabatic process, removing pebbles (which allows the volume to increase) results in a decrease in pressure, as the same number of molecules now have more space to move, colliding with the walls less frequently.
What happens to the temperature of an adiabatic system when work is done on it?
-In an adiabatic system, when work is done (such as expanding the volume by removing pebbles), the temperature decreases because the system loses kinetic energy, which is converted into work, and temperature is a measure of average kinetic energy.
Why does the internal energy of an adiabatic system decrease when work is done on it?
-The internal energy decreases because work is done by the system, which requires energy. Since no heat is added in an adiabatic process, the loss of kinetic energy results in a decrease in internal energy.
What role does a reservoir play in maintaining the temperature of a system during an isothermic process?
-A reservoir acts as an infinitely large heat source or sink that maintains the system's temperature constant. It ensures that any heat lost or gained by the system during expansion or compression is compensated for, keeping the temperature unchanged.
How is the relationship between pressure and volume described during an isothermic process?
-During an isothermic process, the relationship between pressure and volume is described by an inverse proportionality, where the product of pressure and volume (PV) remains constant, following the equation PV = nRT, where n, R, and T are constants.
What is the mathematical formula used to calculate the work done during an isothermic process, as described in the script?
-The work done (W) during an isothermic process is calculated using the formula W = nRT * ln(V2/V1), where n is the number of moles, R is the ideal gas constant, T is the constant temperature, and V1 and V2 are the initial and final volumes, respectively.
How is the heat (Q) added to the system during an isothermic process related to the work done (W)?
-In an isothermic process, the heat added to the system (Q) is equal to the work done by the system (W). This is because the internal energy remains constant, as indicated by the unchanged temperature, and the change in internal energy is the heat added minus the work done (ΔU = Q - W).
Outlines
🔬 Basic Concepts of Isothermal Processes
The paragraph introduces a classic system used for instructional purposes, emphasizing its utility in classrooms. It describes a container with a movable piston and molecules or atoms inside, creating pressure (P1) and occupying a volume (V1) at a certain temperature. The system is in equilibrium, and the macro states (pressure, volume, temperature) can only be defined when the system is uniform. The speaker discusses the concept of an isothermal process, where the temperature remains constant, and explores how removing the weight (pebbles) on the piston would affect the system in an adiabatic scenario, where no heat is exchanged with the environment. The key takeaway is that in an adiabatic process, the removal of weight would lead to an increase in volume and a decrease in pressure, but the temperature would also decrease due to the work done by the system.
🌡️ Isothermal Process with a Reservoir
This paragraph delves into the concept of an isothermal process, explaining how it can be achieved by placing the system in contact with a reservoir, which is an infinitely large body at the same initial temperature (T1). The reservoir ensures that the system's temperature remains constant. The speaker uses the analogy of a small particle (A) and a massive structure (B) to illustrate how the temperature of A would adjust to B's temperature if B is significantly larger. The paragraph also discusses the PV diagram for an isothermal process, showing that as the system's volume increases due to the removal of pebbles, the pressure decreases, but the temperature remains constant. The relationship between pressure and volume in an isothermal process is described as a rectangular hyperbola, with PV being a constant value.
📈 Calculating Work in an Isothermal Process
The speaker explains how to calculate the work done during an isothermal process using the ideal gas law (PV = nRT). By assuming the temperature is constant, the relationship simplifies to P = K/V, where K is a constant. The work done is then the area under the curve on the PV diagram, which can be calculated by integrating P with respect to V from the initial volume (V1) to the final volume (V2). The integral results in nRT times the natural log of V2/V1, indicating that the work done is proportional to the change in volume. This calculation is crucial for understanding the energy changes in thermal systems during isothermal processes.
🔥 Heat Transfer in Isothermal Processes
The final paragraph addresses the question of heat transfer during an isothermal process. The speaker clarifies that since the temperature remains constant, the internal energy does not change. Using the principle that the change in internal energy is equal to the heat added to the system minus the work done by the system, it is concluded that the heat added (Q) is equal to the work done (W). This means that the heat added to the system is exactly what is needed to compensate for the work done, maintaining the constant temperature. The speaker also discusses the convention in thermodynamics for representing this heat transfer, using a downward arrow and the letter Q to denote heat added to the system during the isothermal process.
Mindmap
Keywords
💡Isothermic process
💡Piston
💡Movable ceiling
💡Quasi-static process
💡Macro states
💡Reservoir
💡Adiabatic process
💡Ideal gas law
💡Internal energy
💡PV diagram
💡Work done
Highlights
Introduction to a classic system with a movable piston and molecules creating pressure.
Explaining the importance of equilibrium for defining macro states like volume, pressure, and temperature.
Demonstration of a quasi-static process by slowly removing pebbles to approximate a system close to equilibrium.
Introduction of the isothermic process, where temperature remains constant throughout the process.
Explanation of how removing pebbles would affect volume and pressure in an adiabatic process.
Discussion on the relationship between work done, kinetic energy, and temperature in an adiabatic process.
Clarification that in an adiabatic process, the internal energy decreases as work is done without heat exchange.
Introduction of a reservoir to maintain a constant temperature during the process.
Description of how a reservoir acts as an infinitely large object to maintain the system's temperature.
Explanation of the PV diagram and how it changes during an isothermic process.
Derivation of the relationship between pressure and volume during an isothermic process using the ideal gas law.
Illustration of the rectangular hyperbola representing the isotherm in a PV diagram.
Calculation of work done during an isothermic process using the integral of pressure over volume.
Derivation of the formula for work done as nRT times the natural log of V2 over V1.
Discussion on the heat added to the system during an isothermic process to maintain constant temperature.
Conclusion that the heat added to the system is equal to the work done, as the internal energy remains constant.
Summary of the practical implications of understanding isotherms and adiabatic processes in thermodynamics.
Transcripts
Browse More Related Video

23. The Second Law of Thermodynamics and Carnot's Engine
Thermodynamic Processes (Animation)

Work from expansion | Thermodynamics | Physics | Khan Academy

Carnot cycle and Carnot engine | Thermodynamics | Physics | Khan Academy
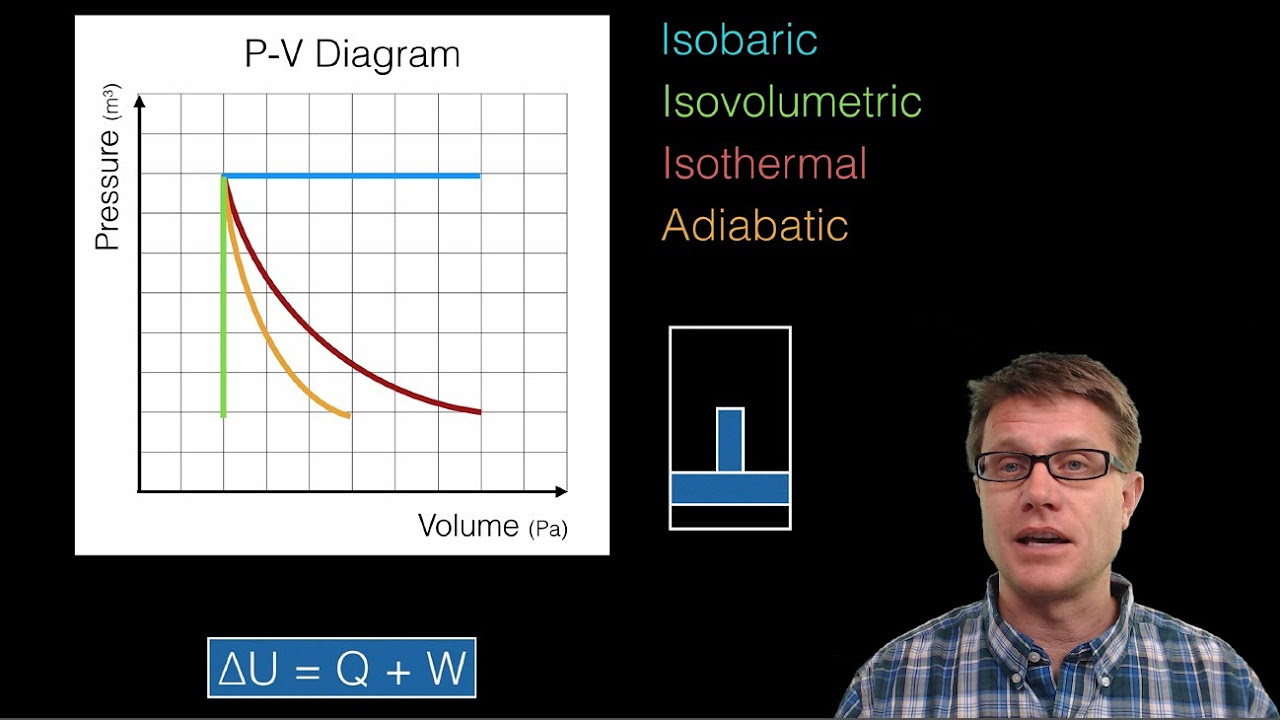
Thermodynamics and P-V Diagrams

AP Physics B - 2013 #5 (Thermodynamics - Work)
5.0 / 5 (0 votes)
Thanks for rating: