Edexcel AS Level Maths: 10.1 Angles in all Four Quadrants (CAST diagram - Trigonometry)

Zeeshan Zamurred
15 Feb 202409:50
EducationalLearning
32 Likes 10 Comments

TLDRThis teaching video covers Chapter 10, Section 1 of an A-level math textbook, focusing on angles in all four quadrants using the CAST diagram. It explains how to measure positive and negative angles from the positive x-axis, and how to determine the trigonometric functions (sine, cosine, and tangent) of these angles. The video includes examples that show how to draw and label angles, calculate acute angles, and express trigonometric ratios in terms of acute angles. Viewers are encouraged to subscribe for more educational content.

Takeaways
  • 📚 The video is a teaching lesson focusing on '10.1 Angles in All Four Quadrants' from a specific A Level Mathematics textbook.
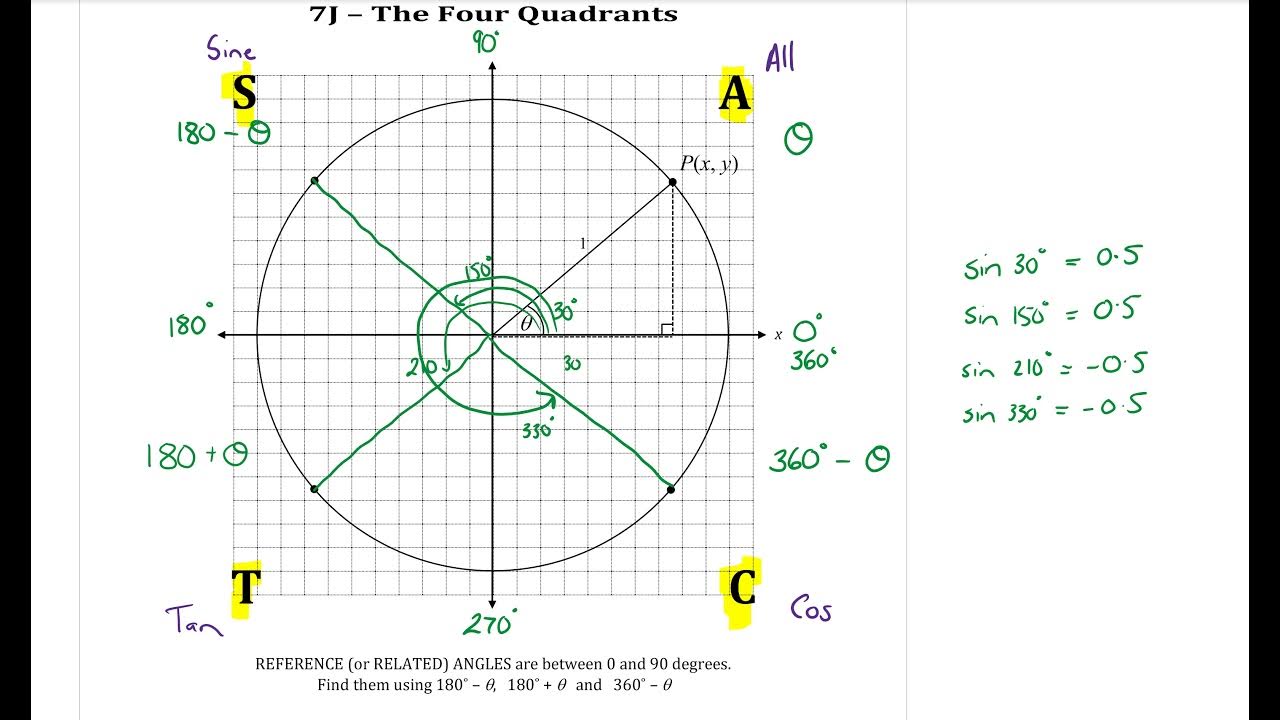
  • 📐 The CAST diagram is introduced as a key tool for understanding the signs of trigonometric functions in different quadrants: Cosine (C), Sine (S), and Tangent (T).
  • 🌐 In the first quadrant, all trigonometric functions (C, S, T) are positive.
  • 📉 In the second quadrant, Cosine is negative while Sine and Tangent are positive.
  • 📈 In the third quadrant, Sine is positive but Cosine and Tangent are negative.
  • 📊 In the fourth quadrant, Tangent is positive while Sine and Cosine are negative.
  • 🔍 Angles are measured from the positive x-axis, with anticlockwise movement representing positive angles and clockwise movement representing negative angles.
  • 📝 The video demonstrates how to calculate trigonometric ratios for angles in different quadrants using the CAST mnemonic.
  • 📌 Examples are provided to illustrate how to determine the acute angle created with the x-axis for given angles of -80°, 200°, 280°, and -160°.
  • 📑 The video includes an exercise to express various angles in terms of trigonometric ratios of acute angles, such as sin(240°), cos(-200°), and tan(-75°).
  • 👍 The instructor encourages viewers to subscribe, like, comment, and turn on notifications for new teaching videos.
Q & A

  • What is the CAST diagram and what does it represent?

    -The CAST diagram is a special diagram used to remember the signs of trigonometric functions in different quadrants. The acronym CAST stands for Cosine, All (referring to sine and tangent), Sine, and Tangent, in that order. It helps to determine which trigonometric functions are positive or negative in each of the four quadrants.

  • How are angles measured in the CAST diagram?

    -Angles are measured from the positive x-axis. Positive angles are measured anticlockwise, and negative angles are measured clockwise.

  • What are the signs of sine, cosine, and tangent in the first quadrant according to the CAST diagram?

    -In the first quadrant, all trigonometric functions are positive, meaning sine, cosine, and tangent are all positive.

  • How does the sign of the trigonometric functions change in the second quadrant?

    -In the second quadrant, sine is positive, but cosine and tangent are negative.

  • What is the process for finding the acute angle created with the x-axis for an angle of -80°?

    -For a negative angle like -80°, you measure clockwise from the positive x-axis. The acute angle created with the x-axis is the positive value of the angle, which in this case is 80°.

  • What is the acute angle created with the x-axis for an angle of 200°?

    -For a positive angle of 200°, measured anticlockwise from the positive x-axis, the acute angle is found by subtracting 180° from 200°, which gives 20°.

  • How is the sine of an angle of 240° expressed in terms of the sine of an acute angle?

    -The sine of 240° is expressed as the negative sine of the acute angle, which is 60°, because sine is negative in the third quadrant.

  • What is the cosine of -200° in terms of the cosine of an acute angle?

    -The cosine of -200° is the negative cosine of the acute angle, which is 20°, because cosine is negative in the third quadrant.

  • How do you express the tangent of -75° in terms of the tangent of an acute angle?

    -The tangent of -75° is the positive tangent of the acute angle, which is 5°, because tangent is positive in the fourth quadrant.

  • What is the significance of the CAST diagram in solving trigonometric problems involving angles in different quadrants?

    -The CAST diagram is crucial for determining the signs of trigonometric functions when solving problems involving angles in different quadrants. It helps to correctly apply the signs to the trigonometric ratios of acute angles to find the values for any given angle.

Outlines
00:00
📐 Introduction to Angles in All Four Quadrants

This section introduces the concept of angles in all four quadrants, referencing Chapter 10, Section 1 of a textbook. It explains the CAST diagram, which helps determine the sign of trigonometric functions in each quadrant. Positive and negative angle measurements are described, along with specific angle calculations such as 180° - Θ, 180° + Θ, and 360° - Θ. Detailed explanations are given for the sign of sine, cosine, and tangent in different quadrants.

05:00
🔄 Examples of Angle Measurements and Acute Angles

The second part provides practical examples of measuring and labeling angles on a diagram. It covers four examples: -80°, 200°, 280°, and -160°. Each example demonstrates how to draw the angle, determine its position on the diagram, and calculate the corresponding acute angle. The explanations clarify how to handle positive and negative angles, and how to find the acute angle related to each given angle.

Mindmap
Keywords
💡CAST Diagram
A mnemonic device used to remember the signs of trigonometric functions in each quadrant of the coordinate plane. CAST stands for Cosine, All, Sine, and Tangent, indicating which trigonometric function is positive in each quadrant. In the script, the CAST diagram is crucial for understanding how angles and their trigonometric functions behave in different quadrants.
💡Quadrants
The four sections of the coordinate plane, divided by the x and y axes. Each quadrant has different rules for the signs of trigonometric functions. The script explains the properties of angles in all four quadrants, including how to measure positive and negative angles from the positive x-axis.
💡Positive Angles
Angles measured counterclockwise from the positive x-axis. In the script, positive angles are essential for understanding the CAST diagram and how trigonometric functions change signs depending on the quadrant.
💡Negative Angles
Angles measured clockwise from the positive x-axis. The script uses negative angles to illustrate how angles can be represented in different quadrants and how their trigonometric functions are affected.
💡Acute Angle
An angle less than 90 degrees. In the script, acute angles are used to simplify and express trigonometric functions in terms of familiar, smaller angles. The acute angle helps in transforming complex angle measurements into more manageable forms.
💡Sine (sin)
A trigonometric function that represents the ratio of the opposite side to the hypotenuse in a right-angled triangle. The script details how the sign of sine changes in different quadrants using the CAST diagram, and provides examples with angles like 240° and 360° - Theta.
💡Cosine (cos)
A trigonometric function that represents the ratio of the adjacent side to the hypotenuse in a right-angled triangle. The script shows how cosine's sign varies across different quadrants and provides examples with angles like -200° and 180° + Theta.
💡Tangent (tan)
A trigonometric function that represents the ratio of the opposite side to the adjacent side in a right-angled triangle. The script explains how tangent changes sign in different quadrants and provides examples like -75° and 180° - Theta.
💡Angle Measurement
The process of determining the size of an angle in degrees, either in a clockwise or counterclockwise direction. The script teaches how to measure angles from the positive x-axis and convert between positive and negative angles, which is fundamental for applying the CAST diagram.
💡Trigonometric Ratios
Ratios of the sides of a right-angled triangle used to define sine, cosine, and tangent. The script uses trigonometric ratios to express angles in terms of acute angles, simplifying the understanding and calculation of trigonometric functions in different quadrants.
Highlights

Introduction to Chapter 10, Section 1 of the A Level Mathematics textbook, focusing on angles in all four quadrants.

Explanation of the CAST diagram, which helps determine the signs of trigonometric functions in different quadrants.

In the first quadrant, cosine, sine, and tangent are all positive.

In the second quadrant, sine and tangent are positive, while cosine is negative.

In the third quadrant, sine is positive, but cosine and tangent are negative.

In the fourth quadrant, tangent is positive, while sine and cosine are negative.

Angles are measured from the positive x-axis, with anticlockwise movement representing positive angles and clockwise movement representing negative angles.

Anticlockwise angles are 90°, 180°, 270°, and 360°, while clockwise angles are -90°, -180°, -270°, and -360°.

Demonstration of how to calculate trigonometric functions for angles like 180° - Theta, 180° + Theta, and 360° - Theta.

For 180° - Theta, sine is positive, cosine is negative, and tangent is negative.

For 180° + Theta, sine is negative, cosine is negative, and tangent is positive.

For 360° - Theta, sine is negative, cosine is positive, and tangent is negative.

Example one involves drawing diagrams to show angles and marking the acute angle made with the x-axis.

Example two involves expressing given angles in terms of trigonometric ratios of acute angles.

For -80°, the acute angle with the x-axis is 80°.

For 200°, the acute angle with the x-axis is 20°.

For 280°, the acute angle with the x-axis is 80°.

For -160°, the acute angle with the x-axis is 20°.

Sine of 240° is expressed as -sin 60°.

Cosine of -200° is expressed as -cos 20°.

Tangent of -75° is expressed as tan 5°.

Transcripts

Browse More Related Video

Trigonometry: How to use the ASTC Rule | The Quadrant | CAST

REFERENCE ANGLES || PRE-CALCULUS

Yr 10 Trigonometry 10 - The four quadrants

Even and Odd Trigonometric Functions & Identities - Evaluating Sine, Cosine, & Tangent

The Unit Circle, Basic Introduction, Trigonometry

How To Find The Exact Values of Trig Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryA-LevelMathematicsAnglesQuadrantsCAST DiagramTrig RatiosAcute AnglesTeaching VideoEducational ContentMath Tutorial