Meeting #5: Lambda Calculus Workshop
TLDRThe video script documents an informal discussion on Lambda calculus and Cartesian closed categories, exploring their theoretical foundations and connections. The conversation begins with technical difficulties and moves into an impromptu lecture on simply typed Lambda calculus, including typing rules and function composition examples. It then delves into category theory, attempting to define a correspondence between Lambda expressions and morphisms in a Cartesian closed category, though the demonstration remains unfinished. The session is interactive, with participants occasionally getting distracted by technical issues and the complexity of the subject matter.
Takeaways
- 😀 The video is a casual discussion about technical topics such as Lambda calculus and Cartesian closed categories.
- 📱 There is an issue with glare and sound quality at the beginning, which seems to be a part of the video's setup.
- 🔍 The participants are trying to troubleshoot technical issues, such as glare and sound, as well as inviting and including participants in the hangout.
- 🤔 The discussion leader admits to not having prepared for the session and plans to 'wing it', indicating an informal and impromptu approach to the content.
- 📝 The script covers the basics of simply typed Lambda calculus, including its rules and the concept of functions within the calculus.
- 🔬 An attempt is made to connect Lambda calculus with Cartesian closed categories, exploring the theoretical underpinnings of functional programming languages.
- 🧠 The conversation delves into the complexities of type theory, with an emphasis on the typing rules and how they apply to expressions and environments.
- 📚 There is a mention of the Omega combinator, a well-known concept in Lambda calculus, but it is noted that it is not relevant to simply typed Lambda calculus.
- 🤷♂️ The participants grapple with the abstract nature of the concepts, acknowledging the difficulty in understanding and explaining the material clearly.
- 🔗 The script attempts to establish a correspondence between Lambda expressions and morphisms in a category, indicating a deeper exploration of the relationship between programming constructs and mathematical categories.
- 🔄 The discussion includes defining a denotation function for Lambda expressions within a Cartesian closed category, although the explanation is complex and not fully fleshed out.
Q & A
What technical issue was initially experienced in the meeting?
-The initial technical issue was glare on the camera, and later there were sound issues with the participants not being able to hear each other clearly.
Who joined the meeting and how were they greeted?
-Kimmy joined the meeting and was greeted with a friendly 'nice hi Kimmy' by the participants.
What was the topic of discussion for the meeting?
-The topic of discussion was Lambda calculus and Cartesian closed categories, and their connection.
What did the participants decide to do while waiting for more people to join the meeting?
-The participants decided to start the meeting with the people present and discuss the topic, despite not having everyone join yet.
Why was there a delay in Greg joining the meeting?
-Greg experienced network issues, which caused him to join and then get dropped from the meeting repeatedly.
What was the confusion regarding the 'join' and 'watch' buttons in the meeting platform?
-The confusion was that Greg was watching the meeting but not participating. It was suggested that he might have clicked the 'watch' button instead of the 'join' button.
What is the Simply Typed Lambda Calculus?
-The Simply Typed Lambda Calculus is a basis for many functional programming languages and is a way to write functions with types. It includes variables, applications, and lambda expressions following specific typing rules.
What is a terminal object in category theory?
-A terminal object in category theory is an object for which there is a unique morphism from every other object in the category to it.
What is an exponential object in category theory?
-An exponential object in category theory is an object that represents functions or morphisms internally, such that there is a natural isomorphism between morphisms of the form A × B → C and A → C^B.
What was the participants' approach to defining a function that maps Lambda expressions to arrows in a category?
-The participants were trying to define a denotation function that takes Lambda expressions and maps them to morphisms in a category, using the typing rules and considering the environment and types as objects in the category.
What was the difficulty in defining the denotation of applications in the category?
-The difficulty was in mapping the application of expressions to morphisms in the category, which required understanding how to use the natural isomorphisms provided by exponential objects and the currying of functions.
What was the final outcome of the meeting?
-The final outcome was inconclusive, as the participants were still in the process of defining the bracket notation and had not yet proven any properties related to the connection between Lambda calculus and Cartesian closed categories.
Outlines
🔊 Sound Issues and Participant Arrival
The paragraph discusses initial technical difficulties with sound during a gathering, possibly a video conference, as participants are arriving. The host is seen troubleshooting the glare from the camera and sound levels, while waiting for more attendees. Kimmy, one of the participants, confirms that she can hear the host clearly. The conversation also includes a discussion about plugging in a device to avoid glare and the possibility of using Google Chat to notify expected participants about the start of the meeting. There's also a casual exchange about work schedules and life balance.
🤔 Technical Support and Participation
This paragraph focuses on the technical support being provided to enable participation in the hangout. A participant named Greg is experiencing issues with joining the conversation; he can only watch but not participate actively. The group discusses potential solutions, such as finding a 'join' button instead of 'watch' and checking Google Chat for notifications. There's a brief mention of the Youtube interface and the need to switch to the hangout interface to participate. The conversation also touches on school-related topics, with a participant mentioning being in school and nearing the end of the semester.
📚 Introduction to Lambda Calculus and Categories
The speaker transitions into a discussion about Lambda calculus and Cartesian closed categories, acknowledging the lack of preparation for the topic. The intention is to introduce simply typed Lambda calculus and its foundational role in functional programming languages. The explanation includes the basic forms of expressions in Lambda calculus, such as variables, applications, and Lambda expressions. The paragraph ends with an introduction to typing rules and types in the context of Lambda calculus.
🔍 Deep Dive into Typing Rules and Lambda Expressions
This paragraph delves deeper into the typing rules of Lambda calculus. It explains the typing judgment and the environment's role in assigning types to variables. The paragraph outlines the rules for typing variables, applications, and Lambda expressions. The discussion includes examples of how to apply these rules to derive types for expressions, emphasizing the importance of understanding the directionality of the rules and the concept of arrow types.
📚 Theoretical Exploration of Lambda Calculus
The speaker continues to explore Lambda calculus, discussing the concept of function composition and its relation to types. The paragraph includes an attempt to prove a property of function composition using typing rules, which involves a detailed examination of the types and expressions involved. The conversation also touches on the idea of variable environments and the typing of Lambda expressions.
🤔 Reflections on Lambda Calculus Complexity
In this paragraph, the speaker reflects on the complexity of the Lambda calculus example provided and whether it was illuminating or necessary. There's a brief discussion about the nature of proofs and proof derivations in type theory. The speaker expresses uncertainty about the practicality of the example and considers avoiding similar complexity in the future.
🔄 Transition to Cartesian Closed Categories
The speaker shifts the focus from Lambda calculus to Cartesian closed categories, discussing the definition and properties of such categories. The paragraph introduces the concept of a terminal object and exponentials, explaining their significance in category theory. The discussion includes the idea of natural isomorphisms and how they relate to functions and morphisms within the category.
🧠 Conceptualizing Cartesian Closed Categories
This paragraph continues the exploration of Cartesian closed categories, focusing on the conceptualization of terminal objects and morphisms. The speaker attempts to define what it means for a type to be terminal and the implications for Lambda expressions as morphisms. The conversation delves into the correspondence between Lambda expressions and categorical structures, considering the need for a unique morphism and the challenges of defining such within the Lambda calculus framework.
🔍 Defining a Denotation for Lambda Expressions
The speaker outlines an approach to define a denotation for Lambda expressions within the context of a Cartesian closed category. The paragraph discusses the process of assigning meanings to environments, types, and expressions based on categorical structures. The conversation includes the use of products, projections, and the application of Currying to interpret Lambda expressions as morphisms in the category.
🤔 Concluding Thoughts on Category Theory and Lambda Calculus
In the final paragraph, the speaker concludes the discussion by reflecting on the connection between category theory and Lambda calculus. The paragraph includes an attempt to define a function that connects the two areas and a consideration of what remains to be proven. The speaker acknowledges the complexity of the task and the need for further exploration, particularly regarding the properties of exponentials in the context of the constructed denotation.
Mindmap
Keywords
💡Lambda calculus
💡Cartesian closed category
💡Type theory
💡Function abstraction
💡Application
💡Environment
💡Typing rules
💡Variable
💡Morphism
💡Denotation
💡Product
Highlights
Introduction to Lambda calculus and its connection to Cartesian closed categories.
Discussion on the preparation for the session and the technical issues faced with sound and glare.
Explaining the concept of simply typed Lambda calculus as a basis for functional programming languages.
Introduction to the grammar of expressions in simply typed Lambda calculus involving variables, applications, and Lambda expressions.
Explanation of typing rules in simply typed Lambda calculus, including variable, application, and Lambda introduction and elimination rules.
Discussion on the challenges of understanding the triviality of basic concepts in the early stages of study.
Attempt to demonstrate a proof in Lambda calculus involving function composition and type theory.
Introduction to category theory and the definition of a Cartesian closed category.
Explanation of terminal objects and exponentials in the context of Cartesian closed categories.
Attempt to establish a correspondence between Lambda expressions and morphisms in a Cartesian closed category.
Discussion on the need for a terminal type in Lambda calculus and its implications.
Exploration of the concept of variables and expressions in Lambda calculus and their analogs in category theory.
Attempt to define a denotation function that maps Lambda expressions to morphisms in a category.
Explanation of the denotation of environments, types, and expressions in the context of category theory.
Discussion on the use of Currying and uncurrying in the interpretation of Lambda expressions as morphisms.
Reflection on the complexity of the construction and the need for further clarification and proof.
Conclusion and acknowledgment of the participants, highlighting the ongoing nature of the exploration.
Transcripts
Browse More Related Video

Martin Hyland: "Algebra & Diagrams in the Lambda Calculus"

The Lambda Calculus, part 1 2 Applied lambda calculi; the simply typed lambda calculus

Lambda (λ) calculus evaluation rules (δ, β, α, η conversion/reduction)

Lambda (λ) Calculus Primer
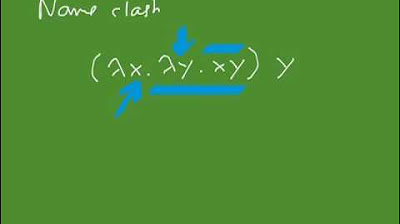
The Lambda Calculus, part 1 1 Syntax and semantics

lambda calculus review
5.0 / 5 (0 votes)
Thanks for rating: