Math Antics - Basic Division
TLDRIn this Math Antics video, you will learn the basics of division, a fundamental arithmetic skill. The lesson starts with simple examples like 9 divided by 3 and explains the concept of remainders with problems such as 9 divided by 4. The video introduces a special division symbol and explains how to use it to solve division problems step-by-step. The method involves setting up the problem, choosing the correct quotient, and dealing with remainders. This foundational knowledge will prepare you for more advanced topics like long division in future lessons. Visit www.mathantics.com for more learning resources.
Takeaways
- 📚 Basic division involves splitting a total into equal groups, like dividing 9 into 3 groups of 3.
- 🔢 Division problems can be solved using multiplication facts, such as knowing that 3 times 3 equals 9.
- 🍪 When dividing, if the total isn't a multiple of the divisor, there will be a remainder, like dividing 9 cookies among 4 kids.
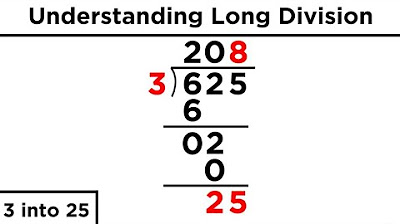
- 📉 The division symbol with a horizontal line and a curved part is used for more complex problems and helps organize the problem into three parts: dividend, divisor, and quotient.
- 📈 The dividend is the number being divided, placed under the horizontal line, and is typically the larger number.
- 🔍 The divisor is the number by which the dividend is divided, placed in front of the division symbol.
- 📉 The quotient is the result of the division, indicating how many units are in each group, and is placed above the horizontal line.
- ❓ The key question in division is 'How many times does the divisor fit into the dividend?', which helps determine the quotient.
- 🚫 If the chosen quotient is too small, the remainder will be larger than the divisor, indicating an incorrect answer.
- 🚫 If the chosen quotient is too large, the multiplication result will exceed the dividend, leading to an impossible remainder.
- 📚 Practice with basic division problems is crucial before moving on to more complex procedures like long division.
Q & A
What is the main topic of the video lesson?
-The main topic of the video lesson is the basics of division.
What is the significance of understanding basic division before learning long division?
-Understanding basic division is crucial because it makes learning long division, which is more complex, much easier.
How is the division problem 9 divided by 3 solved in the video?
-The problem is solved by recognizing that 3 × 3 equals 9, hence 9 divided by 3 is 3.
What is the term used for the number that is being divided in a division problem?
-The number being divided is called the 'dividend'.
What is the term used for the number by which the dividend is divided?
-The number by which the dividend is divided is called the 'divisor'.
What is the term used for the result of a division problem?
-The result of a division problem is called the 'quotient'.
What is the term used for the leftover amount in a division problem?
-The leftover amount in a division problem is called the 'remainder'.
How does the video explain the process of solving a division problem using the division symbol?
-The video explains that you place the dividend under the division symbol, the divisor in front of the division symbol, and the quotient above the division symbol. You then determine how many times the divisor can fit into the dividend to find the quotient and the remainder.
What is the key question to ask when solving a division problem according to the video?
-The key question to ask is 'How many times the divisor will fit into the dividend or almost into it?'
How does the video use the example of 23 divided by 5 to illustrate the division process?
-The video shows that 4 times 5 is 20, which is close to 23 without exceeding it. Subtracting 20 from 23 leaves a remainder of 3, making the quotient 4 and the remainder 3.
What is the importance of ensuring the remainder is less than the divisor in a division problem?
-Ensuring the remainder is less than the divisor is important because it confirms that the division has been done correctly and that the groups are as equal as possible.
What is the next step in learning division after mastering the basics covered in the video?
-The next step is to learn long division, which involves repeating the basic division procedure multiple times.
Outlines
📘 Introduction to Basic Division
The video lesson introduces the basics of division and explains the importance of understanding these fundamentals before learning long division. It starts with a simple example of 9 divided by 3, illustrating that 9 divided by 3 equals 3 because 3 times 3 is 9. The script also touches on fact families and highlights that some division problems, like 9 divided by 4, result in a remainder because 9 is not a multiple of 4. The concept of remainders is explained using the example of dividing 9 cookies among 4 kids.
🔢 Understanding Division with Symbols
This section explains the use of division symbols, starting with the simple division symbol commonly used in fact families. It introduces a more complex division symbol that helps solve harder problems by dividing the division process into three areas: the dividend (number to be divided), the divisor (number of groups), and the quotient (answer). The script demonstrates how to set up a division problem using this symbol, emphasizing the importance of re-writing the problem in this new form before solving it.
🧮 Choosing the Correct Quotient
The focus here is on selecting the correct quotient by asking how many times the divisor can fit into the dividend. Using the example of 9 divided by 4, the script illustrates the process of guessing and checking. It shows that choosing a quotient that is too small results in a large remainder, while a quotient that is too large makes the remainder negative. The correct quotient of 2 is determined, with a remainder of 1, demonstrating the importance of finding a 'just right' quotient.
🍪 Applying Division without Visuals
The paragraph continues the division example, ensuring the viewer understands how to solve it using numbers alone without visual aids like cookies. It reinforces the steps of setting up the problem, choosing the correct quotient, multiplying, and finding the remainder. The script then introduces a new example of 23 divided by 5, walking through the process step by step to find the quotient of 4 with a remainder of 3, and reinforcing the use of the new division symbol.
🔍 Using Multiplication Tables in Division
This section deals with a more challenging division problem: 57 divided by 6. It demonstrates the use of a multiplication table to find the closest multiple of 6 to 57, which is 54. The script explains that 9 is the correct quotient because 9 times 6 equals 54. After subtracting 54 from 57, the remainder is 3, ensuring it is less than the divisor. The process is clearly laid out to show how multiplication tables can aid in finding the quotient.
🏁 Conclusion and Next Steps in Division
The final part of the script summarizes the lesson, emphasizing the importance of mastering basic division problems with remainders before moving on to long division. The video encourages practice and reassures viewers that understanding these basics is crucial for more complex division tasks. It ends with a preview of the next video on long division and a call to action for viewers to visit the Math Antics website for more resources.
Mindmap
Keywords
💡Division
💡Multiplication Facts
💡Fact Families
💡Remainder
💡Dividend
💡Divisor
💡Quotient
💡Long Division
💡Multiplication Table
💡Procedure
💡Goldilocks and the Three Bears
Highlights
Introduction to basic division concepts and its importance for learning long division.
Explanation of division as dividing a total into equal groups.
Use of multiplication facts to simplify division, such as 9 ÷ 3 = 3.
Introduction of division problems that are not part of a fact family, like 9 ÷ 4.
Explanation of remainders in division when the total cannot be evenly divided.
Introduction of the division symbol and its three main areas: dividend, divisor, and quotient.
Description of the dividend as the number being divided.
Description of the divisor as the number by which the dividend is divided.
Description of the quotient as the result of the division.
Procedure for solving division problems by rewriting them in the division symbol format.
Key question in division: 'How many of the divisor will it take to make the dividend or almost the dividend?'
Example of solving 9 ÷ 4 by finding the 'just right' number of 4's to multiply.
Explanation of why a remainder must be less than the divisor.
Demonstration of solving 23 ÷ 5 using the division procedure.
Use of multiplication tables to assist in finding the quotient for 57 ÷ 6.
Final division result of 57 ÷ 6, illustrating the quotient and remainder.
Emphasis on mastering basic division before moving on to long division.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: