Math Antics - Long Division
TLDRThe Math Antics video introduces viewers to the concept of long division, a method for breaking down complex division problems into simpler steps. The script emphasizes the importance of digit-by-digit division, starting from the highest place value and moving right. It guides through examples like dividing 936 by 4, explaining how to handle remainders and combine them with subsequent digits. The video also compares single-step and multi-step division, using 72 divided by 8 and 3 as examples. Tips for mastering long division include memorizing multiplication tables, writing neatly, starting with smaller problems, and checking answers with a calculator. The lesson aims to demystify long division and equip viewers with the skills to tackle larger numbers effectively.
Takeaways
- 📚 Long division is a method to break down complex division problems into a series of simpler steps.
- 🔢 The process involves dividing numbers digit-by-digit, starting from the highest place value and moving to the right.
- 🔄 Division is the reverse of multiplication and addition; it starts from the leftmost digit rather than the rightmost.
- 📉 In long division, if a divisor is too large to divide into the current digit, a zero is placed in the quotient and the process moves to the next digit.
- ✂️ Long division allows for the division of very large numbers by breaking them into manageable parts.
- 📝 It's important to write neatly and keep the division process organized to avoid mistakes.
- 🔍 After completing a long division problem, checking the answer with a calculator can help identify and learn from errors.
- 📉 When there's a remainder from a previous step, it must be combined with the next digit before proceeding with the division.
- 📈 The number of division steps is not always equal to the number of digits in the dividend; it also depends on the size of the divisor.
- 🧠 Memorizing the multiplication table is beneficial for performing long division efficiently.
- 📉 Practice with smaller dividends before moving on to larger problems can help build confidence and skill in long division.
Q & A
What is the purpose of long division according to the video?
-The purpose of long division is to break up a larger division problem into a series of shorter division steps, making it easier to divide numbers of any size.
Why is it important to watch the basic division video before learning long division?
-Watching the basic division video first is important because it provides foundational knowledge that makes learning long division a lot easier.
How does long division differ from basic one-step division?
-Long division differs from basic one-step division in that it involves breaking down the problem into multiple steps, digit-by-digit, rather than solving it all at once.
What is the first step in performing long division as explained in the video?
-The first step in performing long division is to divide the first digit of the dividend by the divisor, ignoring the other digits for now.
How should the answer digit be positioned in long division?
-The answer digit should always be placed directly above the digit that is being divided.
What is the significance of the remainder in long division?
-The remainder is significant in long division because it is carried over to the next step, where it is combined with the next digit of the dividend to continue the division process.
Can you explain the process of bringing down the next digit in long division?
-In long division, after finding the quotient for a particular digit, the next digit of the dividend is brought down next to the remainder to form a new number that will be divided by the divisor in the next step.
What happens if the divisor is too large to divide into the first digit of the dividend?
-If the divisor is too large to divide into the first digit of the dividend, a zero is placed in the answer line for that step, and the process continues with the next digit.
Why is it recommended to practice long division problems starting with smaller dividends?
-Practicing with smaller dividends is recommended because it allows for fewer division steps, making it easier to grasp the concept and build confidence before tackling larger problems.
What is the final step in the long division process as shown in the video?
-The final step in the long division process is to continue the digit-by-digit division until there are no more digits to divide, resulting in a remainder of zero or a final quotient.
Why is it suggested to check answers with a calculator after each practice problem?
-Checking answers with a calculator after each practice problem helps to immediately identify and correct any mistakes, allowing for learning from those errors and also providing practice with calculator usage.
Outlines
📚 Introduction to Long Division
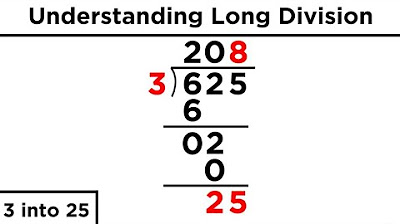
The video introduces long division as a method to break down complex division problems into simpler steps. It emphasizes the importance of understanding basic division before proceeding. Long division allows for the division of very large numbers by thinking about the problem digit-by-digit. The process is demonstrated with a step-by-step example of dividing 936 by 4, illustrating how to handle remainders and combine them with subsequent digits for further division. The video also explains the reverse order of division compared to multiplication and addition, starting from the most significant digit and moving to the least.
🔍 Exploring Long Division with Different Examples
This section of the video script compares long division with basic one-step division problems and demonstrates how the number of division steps can vary depending on the divisor. It uses the example of dividing 72 by 8 and 3 to show that even a seemingly simple problem can require multiple steps. The script also explains the process of dealing with remainders and how to combine them with the next digit in a long division problem. The video proceeds to solve a more complex problem, dividing 315,270 by 5, to illustrate the digit-by-digit approach in action, emphasizing the importance of each step in reaching the correct solution.
🛠 Tips for Mastering Long Division
The final paragraph offers practical advice for those learning long division. It suggests memorizing the multiplication table to facilitate the division process. The importance of neat and organized writing is highlighted to prevent mistakes due to misaligned columns. The script recommends starting with smaller problems and gradually progressing to more complex ones. Lastly, it advises checking answers with a calculator to identify and learn from errors, as well as to gain proficiency with calculators, which is a valuable skill in itself. The video concludes with an invitation to learn more on the Math Antics website.
Mindmap
Keywords
💡Long Division
💡Dividend
💡Divisor
💡Remainder
💡Digit-by-Digit
💡Multiplication Table
💡Subtraction
💡Answer Line
💡Place Holder
💡Graph Paper
Highlights
Introduction to long division as a method for breaking down complex division problems into simpler steps.
Emphasis on the importance of understanding basic division before attempting long division.
Explanation of how long division allows division of very large numbers by breaking them down digit-by-digit.
Clarification that long division starts with the highest place value and works towards the lower ones, unlike addition and multiplication.
Demonstration of dividing a three-digit number by a single-digit number using the digit-by-digit approach.
Illustration of how to handle remainders by combining them with the next digit for subsequent division steps.
Use of multiplication facts to find how many times the divisor can fit into the current number.
Process of multiplying the divisor by the quotient and subtracting from the current number to find the new remainder.
Example of dividing 936 by 4, showcasing the step-by-step method and the importance of placement in the answer.
Highlighting the difference in the number of division steps based on the divisor's size, using 72 divided by 8 and 3 as examples.
Strategy for dealing with a divisor that is too large to fit into the first digit by placing a zero in the quotient.
Division of 315,270 by 5 as an example of a long problem, emphasizing the digit-by-digit process.
Explanation of why zeros are important in long division, even though they represent 'nothing', they serve as placeholders.
The final answer of 315,270 divided by 5 being 63,054, demonstrating the completion of a long division problem.
Advice on practicing long division with smaller problems before moving on to more complex ones.
Suggestion to use graph paper for neat and organized work to prevent mistakes in long division.
Recommendation to check answers with a calculator to learn from mistakes and gain calculator proficiency.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: