Main effects & interactions
TLDRThis instructional video delves into the complexities of main effects and interactions in factorial analysis of variance (ANOVA), a common challenge for students. The presenter uses a simple 2x2 experiment involving sleep deprivation and caffeine effects on memory to illustrate these concepts. The script guides viewers through understanding main effects by comparing average performances across conditions, and interactions by examining the differences between these averages. The example clarifies that caffeine may mitigate the negative impact of sleep deprivation on memory performance.
Takeaways
- 📚 The video aims to explain the concepts of main effects and interactions in factorial analysis of variance, which can be challenging for students.
- 🤔 Main effects and interactions are typically difficult to understand, but practice with journal articles and plots can help in grasping these concepts.
- 📈 The video uses a simple 2x2 factorial design example involving sleep deprivation and caffeine's effect on memory to illustrate the concepts.
- 💤 Sleep deprivation is one factor with two levels: 1 hour and 24 hours, representing different degrees of sleep deprivation.
- ☕ The second factor is the type of supplement, with two levels: a caffeine pill and a placebo pill.
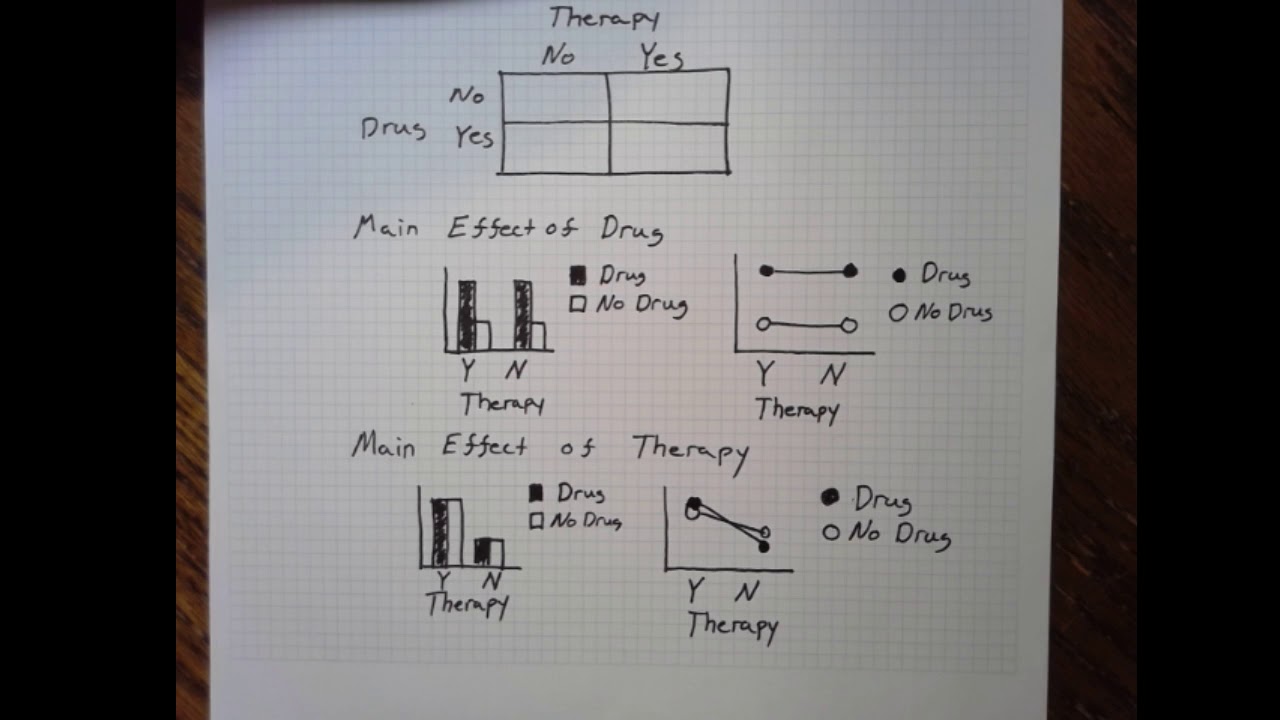
- 📊 In a two-way ANOVA, the main effects are examined by looking at the average performance across the levels of one factor while ignoring the other.
- 🔍 To determine a main effect, compare the average performance for each level of a factor, disregarding the influence of the other factor.
- 🔄 An interaction is identified when the difference in performance between the levels of one factor is different depending on the level of the other factor.
- 🆚 The interaction in the example shows that caffeine seems to mitigate the negative effects of sleep deprivation compared to the placebo group.
- 🧠 Understanding interactions involves recognizing that the performance difference between levels of one factor is influenced by the levels of another factor.
- 💌 The video encourages students to reach out with questions and emphasizes the importance of practice in fully understanding these concepts.
Q & A
What is the main focus of the video script?
-The video script focuses on explaining the concepts of main effects and interactions in factorial analysis of variance (ANOVA), particularly in the context of a 2x2 experimental design.
Why might students struggle with understanding main effects and interactions?
-Students often struggle with these concepts because they can be complex and require an understanding of how different factors and their levels influence outcomes, especially when considering the combined effects.
What is the example used in the script to illustrate the concepts of main effects and interactions?
-The example used is a 2x2 experiment examining the effects of sleep deprivation (1 hour vs. 24 hours) and type of supplement (caffeine pill vs. placebo) on memory performance.
How should one begin to interpret a plot in the context of a two-way ANOVA?
-One should first orient themselves regarding the axes and what the data is showing, before attempting to determine main effects or interactions.
What is the definition of a main effect in the context of ANOVA?
-A main effect is the effect of the levels of one factor while ignoring the levels of the other factor, essentially looking at the impact of one variable on the outcome without considering the influence of the second variable.
What does the script suggest for understanding main effects and interactions?
-The script suggests practicing by examining journal articles and their plots to see if one can identify main effects and interactions in the data presented.
How does the script describe the process of identifying a main effect of sleep deprivation?
-The script describes it as comparing the average performance at 1 hour of sleep deprivation to the average performance at 24 hours, ignoring the type of supplement taken.
What is the purpose of examining the main effect of the type of supplement in the given example?
-The purpose is to determine if there is a difference in average performance between the caffeine group and the placebo group, while ignoring the levels of sleep deprivation.
What does the script define as an interaction in a factorial ANOVA?
-An interaction is defined as the effect where the levels of one factor alter performance across the levels of the other factor, essentially examining if the effect of one variable changes depending on the level of the second variable.
What conclusion can be drawn from the example about the interaction between sleep deprivation and the type of supplement?
-The conclusion is that there is an interaction because the difference in performance between 1 hour and 24 hours of sleep deprivation is significantly different between the caffeine and placebo groups, suggesting that caffeine may alleviate the negative effects of sleep deprivation to some extent.
Outlines
📚 Introduction to Main Effects and Interactions in Factorial ANOVA
This paragraph introduces the concept of main effects and interactions in the context of factorial analysis of variance (ANOVA), a topic that is new to students in their second research methods course. The speaker reassures students that it's common to find these concepts challenging and encourages them to practice by analyzing journal articles. The video aims to clarify these confusing topics, and the speaker offers to answer any questions via email. A simple 2x2 experimental design is introduced to illustrate the concepts, involving sleep deprivation and caffeine's effects on memory.
🔍 Examining Main Effects in Factorial ANOVA
The paragraph delves into how to identify main effects in a factorial ANOVA. It explains that a main effect is the impact of one factor while disregarding the other. The example uses sleep deprivation and supplement type (caffeine or placebo) to demonstrate how to calculate the average performance for each level of the factors and compare them. The speaker emphasizes the importance of understanding the difference between the average performances at different levels of sleep deprivation and the effects of the type of supplement, despite the underlying mathematics being more complex.
🤔 Understanding Interactions Between Factors in Factorial ANOVA
This section focuses on the concept of interactions between factors in a factorial ANOVA. It describes an interaction as the influence of one factor on the performance across the levels of another factor, essentially a 'difference of differences'. Using the sleep deprivation and supplement example, the speaker illustrates how to determine if the performance drop between 1 hour and 24 hours of sleep deprivation is affected by whether participants received caffeine or a placebo. The interaction is identified by comparing the differences in performance between the two levels of sleep deprivation within each supplement group, revealing that caffeine appears to mitigate the negative impact of sleep deprivation.
Mindmap
Keywords
💡Factorial Analysis of Variance (ANOVA)
💡Main Effects
💡Interactions
💡Sleep Deprivation
💡Caffeine
💡Memory Performance
💡2x2 Design
💡Percent Correct
💡Plot
💡Practice
Highlights
Introduction to factorial analysis of variance (ANOVA) and its focus on main effects and interactions.
Assurance that confusion over main effects and interactions is common among students, with an offer of help through practice and review of journal articles.
Explanation of a simple 2x2 factorial design experiment involving sleep deprivation and caffeine's effects on memory.
Description of the experiment's factors: sleep deprivation levels and type of supplement (caffeine or placebo).
Guidance on how to interpret a plot in a factorial ANOVA by understanding axes and data representation.
Definition and method to determine a main effect, focusing on one factor while ignoring the other.
Illustration of calculating the main effect of sleep deprivation by comparing average performances at different deprivation levels.
Similar process for determining the main effect of the supplement, comparing caffeine and placebo groups' average performances.
Introduction to the concept of interaction in factorial ANOVA, examining if one factor influences the performance of the other.
Detailed explanation of how to identify an interaction by comparing the differences in performance between factor levels.
Example provided to show a potential interaction between sleep deprivation and caffeine's mitigating effects.
Clarification that the interaction signifies the difference in performance deterioration rates between caffeine and placebo groups.
Reiteration of the importance of understanding main effects and interactions for correctly interpreting factorial ANOVA results.
Encouragement for students to practice by reviewing journal articles and plots to deepen their understanding of the concepts.
Offer of assistance via email for any questions regarding the video content or the module.
Final summary of the video's content, emphasizing the examination of main effects and interactions in factorial ANOVA.
Transcripts
Browse More Related Video
Factorial Designs: Main Effects & Interactions

Factorial: Main Effects and Interaction Online 2

What's the Best Position to Sleep in? Do we even need a Pillow?

Two-Factor Factorial Design Experiments - ANOVA Model

Statistics 101: Two-way ANOVA with Replication, Marginal Means Graphs

What would happen if you didn’t sleep? - Claudia Aguirre
5.0 / 5 (0 votes)
Thanks for rating: