Factorial Designs: Main Effects & Interactions

S. Wesley Beckwith
12 Nov 201911:30
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into factorial designs, a method of experimentation involving multiple independent variables or 'factors.' It explains how these designs can reveal main effects and interactions between variables, using a 2x2 matrix example to illustrate. The script discusses how to interpret graphical data, identifying main effects through parallel lines and interactions through non-parallel ones, including condensing, fanning, and crossover interactions. A real-life study on encoding specificity further exemplifies these concepts, showcasing the complexity and insights of factorial designs.

Takeaways
  • 🔍 Factorial designs are experiments with multiple independent variables, also known as factors, making them more complex to interpret as more variables are added.
  • 📚 The term 'factorial' comes from the use of multiple factors in the design of the experiment.
  • 🌟 A study by Grant et al. (1998) is used as an example to illustrate encoding specificity, showing the importance of context in learning and memory retrieval.
  • 📈 Factorial designs can be represented in a matrix to visualize the different conditions created by varying independent variables.
  • 🔢 The script introduces '2x2 factorial design' as an example, where '2' represents the number of levels for each independent variable.
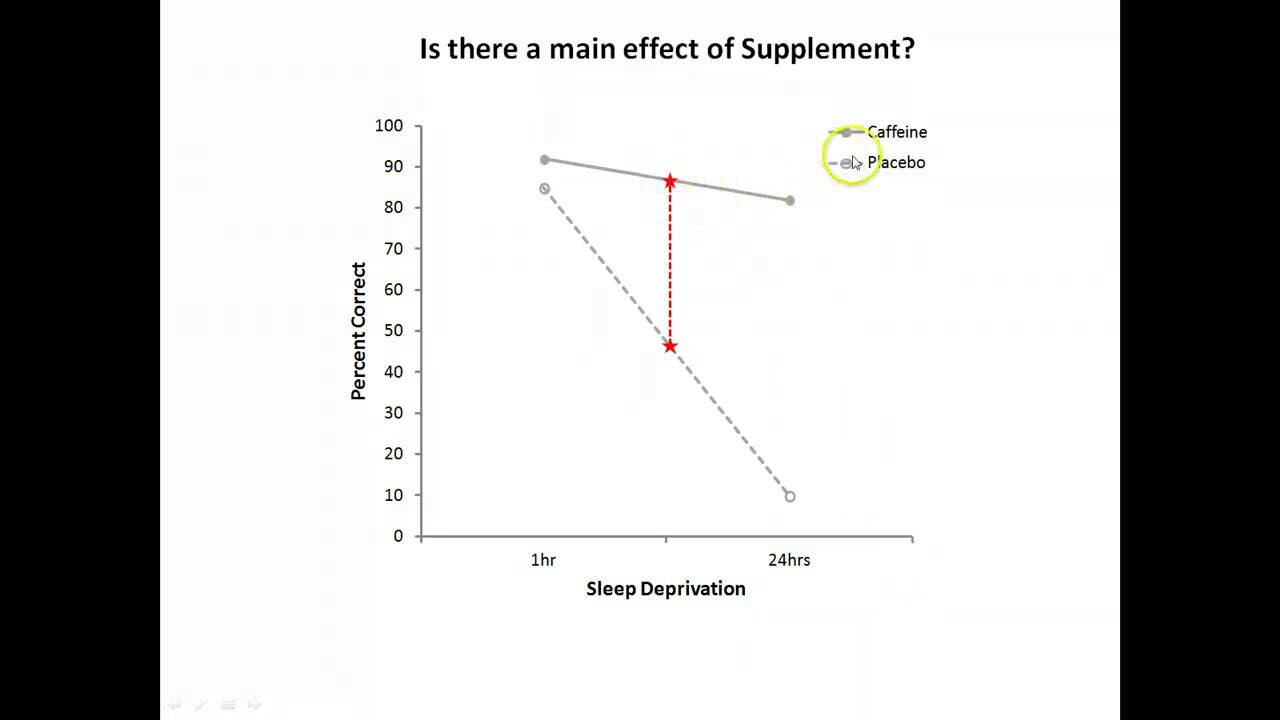
  • 📊 Main effects in factorial designs refer to the impact of an independent variable by itself, while interactions refer to how variables work together.
  • 💊 An example using drug and therapy treatments for depression is given to demonstrate how main effects and interactions can be visualized in a factorial design.
  • 📊 Graphs and bar charts are useful for illustrating the differences in treatment efficacy under various conditions in a factorial design.
  • 🤔 The presence of interactions can be identified by non-parallel lines in graphs, indicating that the effect of one variable changes depending on the level of another.
  • 🔄 A crossover interaction is a specific type of interaction where the effects of the independent variables seem to 'cross over' each other on a graph, flipping their impact.
  • 📝 The script concludes with the importance of identifying main effects and interactions from graphical representations in factorial designs.
Q & A

  • What are factorial designs in the context of experiments or studies?

    -Factorial designs are a type of experiment or study that includes multiple independent variables, which are also known as factors. They allow researchers to examine the effects of these variables and their interactions on a dependent variable.

  • Why is it more challenging to interpret results as more independent variables are added in a factorial design?

    -Adding more independent variables increases the complexity of the design, making it tougher to understand the results due to the higher number of potential interactions and main effects to consider.

  • What is the origin of the term 'factorial design'?

    -The term 'factorial design' comes from the use of multiple factors, which are the independent variables in the study, and the fact that these variables are manipulated in the design.

  • Can you provide an example of a factorial design from the literature?

    -An example from the literature is the study by Grant et al. from 1998, which demonstrated encoding specificity. The study had two independent variables: the study conditions (acquired or noisy environment) and the test conditions (quiet or noisy environments).

  • What is a 2x2 factorial design as mentioned in the script?

    -A 2x2 factorial design is a specific type of factorial design with two independent variables, each having two levels. In the script's example, the two variables are study conditions and test conditions, both with two levels: quiet and noisy.

  • What are main effects and interactions in the context of factorial designs?

    -Main effects refer to the impact of an independent variable on the dependent variable by itself. Interactions, on the other hand, refer to how the effect of one independent variable depends on or is contingent upon the level of another independent variable.

  • How can you visually represent factorial designs?

    -Factorial designs can be visually represented using matrices or graphs. Matrices help in organizing the different conditions created by the levels of independent variables, while graphs can illustrate main effects and interactions through lines or bars.

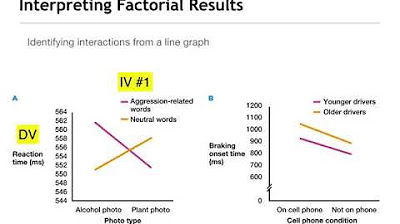
  • What does a parallel line in a graph of a factorial design indicate?

    -Parallel lines in a graph of a factorial design indicate that there are only main effects present, with no interactions between the independent variables.

  • What is a crossover interaction and how can it be identified in a graph?

    -A crossover interaction is a type of interaction where the effect of one independent variable reverses depending on the level of another variable. It can be identified in a graph by the presence of a large 'X' shape, indicating that the lines are not parallel.

  • How can you determine if there is an interaction between independent variables in a factorial design?

    -You can determine if there is an interaction by looking at the graph of the data. If the lines are not parallel, it suggests that there is an interaction between the independent variables. Different patterns of non-parallel lines can indicate different types of interactions.

  • What is the significance of identifying main effects and interactions in a factorial design?

    -Identifying main effects and interactions is crucial for understanding the individual and combined impact of independent variables on the dependent variable. It helps in interpreting the results accurately and drawing meaningful conclusions from the study.

Outlines
00:00
🔍 Introduction to Factorial Designs

This paragraph introduces factorial designs as a type of experiment involving multiple independent variables, also known as factors. It explains the complexity of interpreting results as the number of factors increases. The script references a study by Grant et al., 1998, which demonstrated encoding specificity, using study and test conditions as independent variables in a 2x2 factorial design. The paragraph emphasizes the importance of diagramming factorial designs in a matrix to visualize different conditions and the concept of main effects and interactions, which are central to understanding factorial designs.

05:01
📊 Understanding Main Effects and Interactions

The second paragraph delves deeper into the concepts of main effects and interactions within factorial designs. It uses a hypothetical example of drug and therapy treatments for depression to illustrate how to represent these variables in a matrix and graph. The paragraph explains that main effects show the influence of a single variable, while interactions occur when the effect of one variable is contingent upon another. It also describes how to visually identify these effects through bar and line graphs, highlighting different scenarios where either the drug, therapy, or both have main effects without interaction, or when there is a significant interaction between them.

10:03
📚 Identifying Main Effects and Interactions in Graphs

The final paragraph focuses on how to identify main effects and interactions by analyzing graphs. It explains that parallel lines in a graph indicate main effects, while non-parallel lines suggest an interaction. The paragraph provides examples of different types of interactions, including condensing, fanning, and crossover interactions, and how they appear on a graph. It also revisits the Grant et al., 1998 study to demonstrate a crossover interaction with study and test conditions. The summary includes a step-by-step guide on how to draw and interpret graphs for a 2x2 factorial design, emphasizing the visual distinction between main effects and various types of interactions.

Mindmap
Keywords
💡Factorial designs
Factorial designs are a class of experiments or studies that involve multiple independent variables, which can be two, three, or more. The complexity of understanding the results increases with the number of variables added. In the context of the video, factorial designs are crucial for examining how different factors, such as study conditions and memory tests, interact and influence outcomes. The script uses a 2x2 factorial design example to illustrate the concept, where '2x2' indicates two levels for each of the two independent variables.
💡Independent variables
Independent variables, also known as factors, are the variables manipulated by the researcher in an experiment to observe their effects on the dependent variable. In the video, the study conditions (quiet or noisy) and the type of memory test environment (acquired or noisy) are independent variables. Their effects are analyzed to understand how they influence memory retention, which is central to the theme of the video.
💡Main effects
Main effects refer to the impact of an independent variable on the dependent variable when considered in isolation from other variables. The video explains main effects by discussing how a drug treatment or a therapy treatment might independently affect the treatment efficacy for depression. The script uses graphical representations to illustrate the concept, showing how the presence or absence of a treatment can affect outcomes.
💡Interactions
Interactions occur when the effect of one independent variable on the dependent variable is contingent upon the level of another independent variable. The video script provides examples of interactions, such as the drug and therapy example, where the combined effect is different from the sum of their individual effects. The concept is further clarified with a crossover interaction from the Grant et al. study, where study and test conditions interact to affect memory performance.
💡Encoding specificity
Encoding specificity is a concept demonstrated in the Grant et al. 1998 study mentioned in the video. It refers to the idea that the context in which information is learned can affect how well it is recalled. The video uses this concept to explain the importance of factorial designs in understanding how different study and test environments can interact to influence memory performance.
💡Matrix
In the context of the video, a matrix is used as a diagrammatic tool to organize and visualize the different conditions created by the levels of independent variables in a factorial design. The script describes how to diagram a 2x2 factorial design by placing one independent variable on each side of the matrix, allowing for a clear visualization of all possible experimental conditions.
💡Bar graph
A bar graph is a type of chart used in the video to represent hypothetical results of factorial designs. It visually compares the effects of different treatments or conditions, such as drug versus therapy, on a dependent variable like treatment efficacy. The script uses bar graphs to illustrate main effects and interactions, with filled and unfilled bars representing different conditions.
💡Line graph
A line graph is another graphical representation used in the video to depict the relationship between independent variables and a dependent variable. It is particularly useful for showing the main effects and interactions in a factorial design. The script explains how parallel lines in a line graph indicate no interaction, while non-parallel lines suggest an interaction effect.
💡Crossover interaction
A crossover interaction is a specific type of interaction where the effect of one independent variable reverses depending on the level of another variable. The video uses the Grant et al. study as an example, where the study and test conditions create a crossover interaction, evident when the performance in quiet and noisy environments switches depending on the study environment.
💡Condensing interaction
A condensing interaction is a type of interaction where the effect of one independent variable diminishes or becomes less pronounced as the level of another variable increases. The video script describes this concept using a line graph, where non-parallel lines indicate that the effect of one variable is dependent on the level of another, showing an interaction.
💡Fanning interaction
A fanning interaction is another type of interaction depicted in the video, where the effect of one independent variable diverges or fans out as the level of another variable increases. This is shown in the script with non-parallel lines in a line graph, indicating that the impact of one variable changes with the level of the other variable.
Highlights

Factorial designs involve multiple independent variables, making them complex to interpret.

The term 'factorial' comes from the use of multiple factors or independent variables in the design.

An example from Grant et al. (1998) demonstrates encoding specificity in learning contexts.

The study conditions and test environments are two independent variables in the Grant et al. study.

A 2x2 factorial design implies two independent variables with two levels each.

Main effects and interactions are two key aspects revealed by factorial designs.

Main effects show the impact of one independent variable on its own.

Interactions occur when the effect of one variable depends on the level of another.

A hypothetical example compares drug and therapy treatments for depression.

Diagrams and graphs are useful for visualizing the effects in factorial designs.

A bar graph can illustrate the efficacy of treatments with filled and open bars.

Line graphs can also represent treatment effects with different markers for conditions.

Identifying main effects involves looking for parallel lines in graphs.

Interactions are indicated by non-parallel lines in graphical representations.

A condensing interaction and a fanning interaction are types of interactions with non-parallel lines.

A crossover interaction results in an 'X' pattern on a line graph, indicating flipped effects.

The Grant et al. study showed a crossover interaction between study and test conditions.

Identifying main effects and interactions is crucial for understanding factorial designs.

Transcripts

Browse More Related Video

Factorial Designs Describing Main Effects and Interactions

Factorial: Main Effects and Interaction Online 2

Two-Factor Factorial Design Experiments - ANOVA Model

2^k Factorial Designs Experiment - ANOVA Model

Main effects & interactions

Full Factorial Design (DoE - Design of Experiments) Simply explained

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Factorial DesignExperimentationIndependent VariablesMain EffectsInteraction EffectsEncoding SpecificityStudy ConditionsMemory TestTreatment EfficacyCognitive TherapyDepression Treatment