13 - ANOVA Basics - The Grand Mean

Math and Science
13 Mar 201818:52
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the concept of the grand mean in the context of Analysis of Variance (ANOVA), a statistical method used to compare the means of three or more groups. The instructor explains the grand mean as the average of all sample means, emphasizing its role as a common baseline for comparison. The script guides through the mathematical notation and calculation of the grand mean using a real-life example of the average age of marriage for females in different US states. The detailed explanation aims to demystify ANOVA's equations and prepare viewers for further statistical analysis.

Takeaways
  • 📚 The lesson focuses on the Analysis of Variance (ANOVA), explaining its components and calculations step by step.
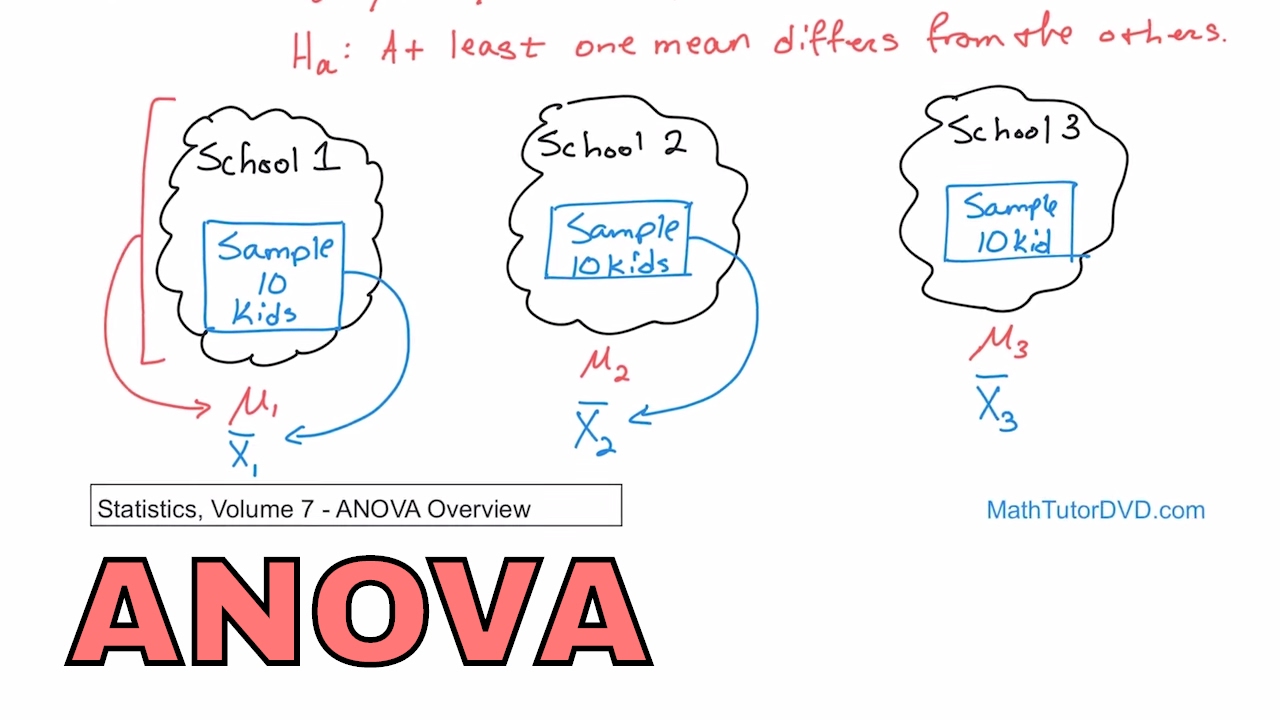
  • 👰 The practical example used is the average age of marriage for females in New York, Texas, and Oregon, with data provided for each state.
  • 🔍 The goal is to determine if the average age of marriage is the same across these three states using an ANOVA test at a 90% confidence level.
  • 🧐 The populations being studied are the entire female populations of the three states, but due to practicality, only samples are taken.
  • ℹ️ The concept of the 'grand mean' is introduced as the average of all sample means, serving as a common baseline for comparison.
  • 📈 The grand mean is calculated by summing all data points from the samples and dividing by the total number of samples.
  • 📝 The mathematical notation for calculating the grand mean is explained in detail to help understand the summation process.
  • 🔢 The actual calculation of the grand mean for the given data results in an average of 19.46667, representing the average age of marriage across all three states.
  • 🔄 The process involves understanding summation symbols and algebraic expressions, which are crucial for further ANOVA calculations.
  • 🚀 The lesson emphasizes the importance of grasping these foundational concepts before moving on to more complex parts of ANOVA testing.
  • 🔍 The next steps will involve comparing individual sample means to the grand mean to identify any significant deviations among the populations.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is the concept of Analysis of Variance (ANOVA), specifically focusing on the calculation of the grand mean in the context of comparing the average age of marriage among females in different states.

  • What is the grand mean in the context of ANOVA?

    -The grand mean is the overall average of all the data points from all the groups or populations being studied. It serves as a common baseline to compare the sample means of each group.

  • Why is the grand mean important in ANOVA?

    -The grand mean is important because it provides a reference point to compare the sample means of each group. It helps in determining if there are any significant differences between the group means.

  • What is the null hypothesis in the context of this ANOVA problem?

    -The null hypothesis is that the average age of marriage for females in New York, Texas, and Oregon is equal, meaning there is no significant difference between the average ages in these three states.

  • What is the alternate hypothesis in this ANOVA problem?

    -The alternate hypothesis is that at least one of the average ages of marriage for females in New York, Texas, and Oregon is different from the others.

  • What is the significance level mentioned in the script, and what does it represent?

    -The significance level mentioned in the script is 0.1, which represents a 90% level of confidence. It is the probability of rejecting the null hypothesis when it is actually true.

  • How many samples were taken from each of the three populations in the example provided?

    -Ten samples were taken from each of the three populations: New York, Texas, and Oregon.

  • What are the populations in this ANOVA example?

    -The populations in this example are the entire female population of New York, Texas, and Oregon, specifically focusing on the age at which they get married.

  • Why can't we sample the entire population in an ANOVA test?

    -Sampling the entire population is not feasible due to constraints such as cost and time. Therefore, a representative sample is taken from each population to perform the analysis.

  • How is the grand mean calculated mathematically?

    -The grand mean is calculated by summing all the data points from all the samples and dividing by the total number of samples across all populations.

  • What does the script suggest about the complexity of the equations used in ANOVA?

    -The script suggests that while the equations used in ANOVA may appear complex and intimidating, the underlying concept, such as the grand mean, is actually quite simple and involves averaging the sample means or all data points together.

Outlines
00:00
📚 Introduction to Analysis of Variance (ANOVA)

The script begins with an introduction to the concept of Analysis of Variance (ANOVA), focusing on the basics. The instructor plans to dissect the components and calculations of ANOVA in detail over several lessons. The context for the problem is set with a real-world example of analyzing the average age at which females get married in three different states: New York, Texas, and Oregon. The data for this analysis is presented, and it's explained that the goal is to determine if there's a significant difference in the average age of marriage across these states using a sample of 10 individuals from each state. The concept of the grand mean is introduced as the first component of the ANOVA calculation.

05:02
🔍 Understanding the Grand Mean in ANOVA

This paragraph delves deeper into the concept of the grand mean, which is the mean of all sample means from different populations being compared. The instructor clarifies that the grand mean is calculated by averaging the individual sample means or by summing all data points and dividing by the total number of samples. The mathematical notation and formula for calculating the grand mean are explained in detail to help the audience understand the process and notation used in statistical analysis. The importance of the grand mean as a common baseline for comparison is emphasized.

10:03
📘 Calculating the Grand Mean: A Step-by-Step Approach

The instructor provides a step-by-step guide on how to calculate the grand mean using the given data. This includes summing all individual data points from each population and dividing by the total number of samples, which in this case is 30 (10 samples from each of the three states). The summation notation is explained, and the process of adding up all values from each population is described in detail. The calculation is demonstrated with the actual data provided, emphasizing the methodical approach to summing and averaging to arrive at the grand mean.

15:03
🔢 Final Calculation of the Grand Mean and its Significance

The final calculation of the grand mean is presented, with all data points from the three populations summed and divided by 30 to get an average of 19.4666667. The instructor highlights the importance of this value as it serves as a representative average of the average age of marriage across the three states. It is emphasized that this grand mean will be used as a baseline to compare the sample means of each state in subsequent parts of the ANOVA test. The summary underscores the simplicity of the grand mean concept and its critical role in the analysis.

Mindmap
Keywords
💡Analysis of Variance (ANOVA)
Analysis of Variance (ANOVA) is a statistical method used to compare the means of three or more groups to determine if there are any statistically significant differences between them. In the video, ANOVA is the central theme as the instructor discusses how to perform this test to compare the average age of marriage among females in New York, Texas, and Oregon. The script mentions that even if the test indicates a difference, it won't specify which groups differ, highlighting a limitation of ANOVA.
💡Grand Mean
The Grand Mean is the average of all sample means in an ANOVA test. It serves as a common baseline for comparing the means of different groups. In the script, the instructor explains that the Grand Mean is calculated by averaging all the data points from the different populations together, which in this case are the ages at which females get married in the three states mentioned.
💡Sample Mean
A Sample Mean is the average of a sample of data collected from a population. The script refers to the sample means of the ages at which females get married in New York, Texas, and Oregon. These sample means are then used to calculate the Grand Mean and are later compared against it to determine if there is a significant variance among the groups.
💡Null Hypothesis
The Null Hypothesis is a statement of no effect or no difference that researchers test in an experiment. In the context of the video, the Null Hypothesis is that the average age of marriage for females in New York, Texas, and Oregon is the same. The instructor emphasizes that the ANOVA test can only tell us if at least one mean is different, not which one.
💡Alternate Hypothesis
The Alternate Hypothesis is what researchers believe might be true if the Null Hypothesis is false. In the script, the Alternate Hypothesis is that at least one of the average ages of marriage among the three states is different. This is what the ANOVA test is designed to evaluate.
💡Population
In statistics, a Population refers to the entire group that is the subject of a study. The script uses the term to refer to the entire female population of New York, Texas, and Oregon, whose average ages of marriage are being studied. The populations are the groups being compared in the ANOVA test.
💡Sample Size
Sample Size is the number of observations or elements in a sample. In the video, the sample size is consistently 10 for each of the three populations being studied (New York, Texas, and Oregon), which means each state's data is based on the ages of 10 females.
💡Significance Level
The Significance Level is the probability threshold at which the Null Hypothesis is rejected. The script mentions a 0.1 level of significance, which corresponds to a 90% level of confidence. This means that if the test results indicate a difference, there is a 90% confidence that the difference is not due to random chance.
💡Summation Symbol
The Summation Symbol (Σ) is used in mathematics to denote the sum of a sequence of numbers. In the script, the instructor uses the summation symbol to explain how to calculate the Grand Mean by adding all the data points from the different samples and then dividing by the total number of samples.
💡Degrees of Freedom
Degrees of Freedom in statistics refer to the number of values that are free to vary in a calculation. While not explicitly mentioned in the script, the concept is implied when discussing the total number of samples, which affects the calculation of the Grand Mean and is a critical component in ANOVA calculations.
💡Rounding Error
Rounding Error occurs when numerical values are rounded to a certain number of decimal places, potentially introducing a small error into the calculation. The instructor in the script is careful to carry many decimal places when calculating the Grand Mean to avoid any rounding errors that might affect the accuracy of the ANOVA test.
Highlights

Introduction to the concept of Analysis of Variance (ANOVA) and its application to compare the average age of marriage among females in three different states.

Explanation of the problem setup involving the ages at which females get married in New York, Texas, and Oregon.

Clarification that the entire female populations of the states are the populations of interest, not just the sampled individuals.

Introduction of the grand mean as the simplest and most fundamental component of ANOVA calculations.

Description of the process to calculate the grand mean by averaging all sample means or by summing all data points and dividing by the total number of samples.

The null hypothesis is that the average age of marriage is the same across all three states, while the alternative hypothesis suggests at least one mean is different.

Emphasis on the limitation that ANOVA does not identify which specific group means differ, only that there is a difference.

Explanation of the mathematical notation and symbols used in ANOVA calculations, including the grand mean represented as \( \bar{X}_{..} \).

Detailed breakdown of the summation notation and how it is used to calculate the grand mean.

The importance of understanding the mathematical equations and notation for grasping the concepts of ANOVA.

Demonstration of calculating the grand mean for the given data set by adding all ages and dividing by the total number of samples.

The calculated grand mean is presented as 19.46666667, representing the average age of marriage across the three states.

The grand mean serves as a common baseline to compare the sample means of each state in subsequent ANOVA calculations.

The transcript provides a step-by-step guide to understanding the calculations by hand before using tools like Excel.

The next steps in the ANOVA process will involve comparing sample means to the grand mean to determine if there are significant differences.

Encouragement for learners to follow along to the next lesson for further breakdown of ANOVA calculations.

Transcripts

Browse More Related Video

ANOVA 1: Calculating SST (total sum of squares) | Probability and Statistics | Khan Academy

SPSS (9): Mean Comparison Tests | T-tests, ANOVA & Post-Hoc tests

12 - Analysis of Variance (ANOVA) Overview in Statistics - Learn ANOVA and How it Works.

Statistics: Sample vs. Population Mean

One Way ANOVA (Analysis of Variance): Introduction | Statistics Tutorial #25 | MarinStatsLectures

Sampling Distributions: Introduction to the Concept

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ANOVAGrand MeanStatistical AnalysisMarriage AgesEducational ContentData ComparisonHypothesis TestingSample SizePopulation StudyStatistical Concepts