Math 119 Chapter 9 part 3
TLDRThis instructional video script covers matched pairs analysis in statistics, focusing on hypothesis testing for dependent samples. The instructor guides through converting two-sample problems into single-sample problems by calculating differences, using t-tests for hypothesis testing, and constructing confidence intervals. Real-world examples, such as weather forecasting accuracy and the superstition of Friday the 13th, are used to illustrate concepts. The script emphasizes consistency in subtraction method and understanding the implications of positive or negative results in hypothesis testing.
Takeaways
- 📚 The lecture is transitioning from a previous section to match pairs, with a discrepancy in section numbers between the notes and the book.
- 🕒 Time constraints mean the final section of the homework will not be covered in the lecture, focusing instead on a quick overview before moving to Chapter 10.
- 🔢 The method for analyzing matched pairs involves calculating the difference between paired sample values to test claims about the population difference and construct confidence intervals.
- 📉 The process involves turning a two-sample problem into a one-sample problem by subtracting the samples, simplifying the analysis as done in previous chapters.
- ⚖️ The sample data for matched pairs should be dependent, often representing before-and-after scenarios, and should ideally follow a normal distribution for the method to be valid.
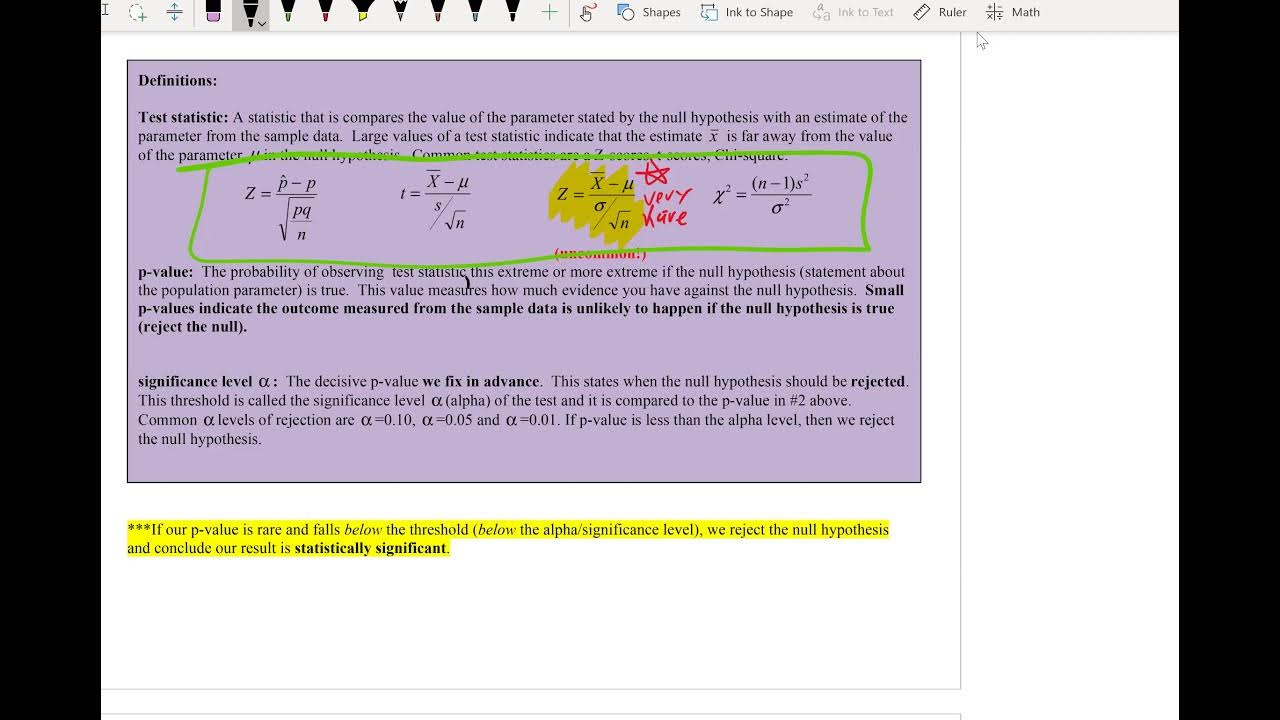
- 🎯 The mean difference (d̄) is a crucial parameter in hypothesis testing for matched pairs, with the null hypothesis typically stating no significant difference (μd = 0).
- 📉 The standard deviation of the differences (sd_d) is used alongside the mean difference to calculate the test statistic for hypothesis testing.
- 🧭 Consistency is key when subtracting paired data; whether it's 'top minus bottom' or 'before minus after', the method should be applied uniformly.
- 📊 The use of a calculator is emphasized for finding the test statistic, standard deviation, and ultimately the p-value to make statistical decisions.
- 🅰️ The significance level (α) is commonly set at 0.05 for hypothesis testing, determining whether to reject the null hypothesis based on the p-value.
- 📝 The script provides step-by-step instructions on conducting a t-test for matched pairs, including entering data, calculating the test statistic, and interpreting the p-value.
- 📉 The script also covers constructing confidence intervals from the data, which can be used to assess whether there is a significant difference between matched pairs.
Q & A
What is the discrepancy between the notes and the textbook regarding the chapter and section numbers?
-The discrepancy is that the notes refer to section 9.4, but the instructor believes it should be 9.3 in the textbook.
Why might the instructor not cover the final section of the homework?
-The instructor does not believe there will be enough time to cover the final section, which is the last part over chapter 9 and 10 in the notes.
What type of data is being discussed in the context of matched pairs?
-Matched pairs data often involves before and after measurements, and it comes from the same sample group, making the samples dependent.
What is the significance of calculating the difference between two values in matched pairs?
-The difference between the two values is used to test claims about the population difference and to construct confidence intervals for these population differences.
What are the conditions for using matched pairs t-test?
-The conditions include having dependent sample data, random samples, a large sample size (n > 30), or differences that approximately follow a normal distribution in the population.
What is the parameter being tested in the hypothesis tests for matched pairs?
-The parameter being tested is the mean difference (mu_d), which is the mean value of the differences in the population of all matched pairs.
What is the general form of the null hypothesis for matched pairs t-tests?
-The general form of the null hypothesis is that the mean difference (mu_d) is equal to zero, indicating no significant difference.
Why is it important to be consistent when subtracting the samples in matched pairs?
-Consistency is important to avoid confusion and to ensure that the direction of the difference (whether it's less than or greater than zero) is clear and interpretable.
What does the instructor mean by 'quick hitter video'?
-A 'quick hitter video' refers to a brief instructional video that covers the material quickly and concisely, without going into extensive detail.
How does the instructor approach the problem of testing the claim about the mean difference in the weather forecast example?
-The instructor demonstrates how to convert two samples into one by subtracting them, calculate the sample mean difference, and then use a t-test to determine if there is sufficient evidence that the mean difference is not zero.
What is the conclusion of the weather forecast example regarding the accuracy of the forecasts?
-The conclusion is that there is insufficient evidence to support the claim that the mean difference is not zero, suggesting that the forecasts may be accurate.
What significance does the p-value have in determining the outcome of a hypothesis test?
-The p-value indicates the probability of observing the test results under the null hypothesis. If the p-value is less than the significance level (alpha), it suggests that the results are statistically significant, and the null hypothesis is rejected.
How does the instructor handle the second example regarding the number of hospital admissions due to motor vehicle crashes?
-The instructor guides through the process of calculating the mean difference and performing a t-test to determine if there is a significant difference in the number of accidents between Friday the 6th and Friday the 13th.
What is the conclusion of the hospital admissions example regarding the belief that Friday the 13th is unlucky?
-The conclusion is that there is sufficient evidence to support the claim that the mean difference in accidents is less on Friday the 6th compared to Friday the 13th, suggesting that Friday the 13th may indeed be considered unlucky in this context.
How does the instructor demonstrate constructing a confidence interval for matched pairs?
-The instructor shows the process of entering the data, calculating the mean difference, and using the t interval function on a calculator to construct a 95% confidence interval.
What does it mean if zero is within the confidence interval for matched pairs?
-If zero is within the confidence interval, it suggests that there is no significant difference between the means of the matched pairs, and the null hypothesis (that there is no difference) cannot be rejected.
Outlines
📚 Introduction to Matched Pairs Hypothesis Testing
The script begins with an introduction to the topic of matched pairs hypothesis testing, found in chapter 9.3 of the book and 9.4 in the notes. The instructor clarifies that they will not cover the final section of the homework due to time constraints. The focus is on methods for testing claims about population differences using matched pairs of sample values, often representing before and after scenarios. The process involves calculating the difference between the two values and using these differences for hypothesis testing and constructing confidence intervals. The instructor emphasizes that the approach will be consistent with previous chapters, transforming a two-sample problem into a one-sample problem by calculating the differences between the pairs.
🔢 Calculating Mean Differences and Hypothesis Testing
The second paragraph delves into the specifics of calculating the mean difference between matched pairs, denoted as d-bar, and using it for hypothesis testing. The null hypothesis (H0) typically states that there is no significant difference (mu_d equals zero), while the alternative hypothesis (Ha) varies based on the claim being tested. The instructor demonstrates how to calculate d-bar using a set of temperatures, both actual and predicted, and how to perform a t-test using a calculator. The process includes entering the differences into the calculator, finding the standard deviation, and computing the test statistic to determine if the forecast is accurate.
📉 Hypothesis Testing for Weather Forecast Accuracy
In this paragraph, the instructor applies the hypothesis testing method to determine if there is sufficient evidence to conclude that the mean difference in weather forecasts is not zero, indicating forecast accuracy. The data provided includes actual and predicted low temperatures for five days. The instructor guides through the process of calculating the sum of differences, finding the sample mean difference (d-bar), and setting up the hypothesis test. The test statistic is computed, and a p-value is determined, leading to the conclusion that there is insufficient evidence to claim the forecasts are inaccurate, as the p-value is greater than the significance level (alpha = 0.05).
🏥 Testing the 'Unluckiness' of Friday the 13th
The script continues with an example of testing the superstition that Friday the 13th is unluckier, using data on hospital admissions due to motor vehicle crashes. The hypothesis is that there is a higher average of crashes on Friday the 13th compared to the sixth. The instructor shows how to calculate the mean difference and perform a one-tailed t-test, given the negative differences indicating fewer accidents on the 13th. The resulting p-value is found to be 0.021, leading to the rejection of the null hypothesis and acceptance of the alternative, suggesting that Friday the 13th is indeed associated with a higher average of crashes.
📊 Constructing a Confidence Interval for Hypothesis Testing
The final paragraph of the script discusses constructing a confidence interval to test for the existence of a mean difference. Using the matched pairs approach, the instructor demonstrates how to calculate the confidence interval for the differences in accidents between two Fridays. The confidence interval is computed using the t-interval function on the calculator, yielding a range that includes zero. According to the guidelines for hypothesis testing with confidence intervals, if zero is within the interval, it indicates that there is not enough evidence to claim a significant difference between the means, thus the null hypothesis that there is no difference cannot be rejected.
📌 Conclusion and Offering Help for Chapter Nine
The instructor concludes the video by summarizing the activities covered in the video, which focused on the end of chapter nine and the notes. They mention that they have chosen not to cover certain sections to save time and encourage students to reach out for help if needed. The video serves as a final review for the concepts of matched pairs hypothesis testing and confidence intervals, aiming to clarify the process and calculations involved.
Mindmap
Keywords
💡Matched pairs
💡Dependent samples
💡Mean difference (d)
💡Null hypothesis (H0)
💡Alternative hypothesis (H1)
💡Confidence interval
💡Test statistic
💡P-value
💡Significance level (alpha)
💡Random samples
Highlights
The lecture begins with a clarification of the section to be covered, noting that not all homework sections will be discussed due to time constraints.
The focus is on methods for interest in matched pairs, often used for before-and-after comparisons.
The process involves calculating the difference between two values from matched pairs and using these differences for hypothesis testing and constructing confidence intervals.
The approach parallels previous chapters, transforming a two-sample problem into a one-sample problem by subtracting the samples.
The importance of the mean difference (mu_d) is emphasized for hypothesis testing in matched pairs.
The null hypothesis typically assumes no significant difference (mu_d = 0), while the alternative hypothesis explores significant differences.
Consistency in the method of subtraction (e.g., top data minus bottom data) is advised for clarity and ease of understanding.
The use of a calculator for hypothesis testing is introduced, streamlining the process for students.
An example problem involving actual versus predicted low temperatures is used to demonstrate the testing process.
The calculation of the sample mean difference (d_bar) and its significance in hypothesis testing is explained.
The process of determining the p-value and its role in deciding whether to reject the null hypothesis is covered.
A second example regarding hospital admissions from motor vehicle crashes on Friday the 6th versus Friday the 13th is presented.
The concept of constructing a confidence interval for the mean difference is introduced, with an example provided.
The use of a calculator to compute the test statistic and p-value for the Friday the 13th example is demonstrated.
The conclusion from the examples is that the evidence must be evaluated to determine if there is a significant difference, supporting or not supporting the claims.
The importance of the perspective in interpreting results, such as 'greater than' or 'less than', is highlighted.
The lecture concludes with a reminder of the importance of method consistency and a prompt for students to seek help if needed.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: