Uniform Circular Motion: Crash Course Physics #7
TLDRThis video explains the physics of circular motion, using carnival rides and human centrifuges as examples. It covers key concepts like velocity, which is tangent to the circle; centripetal acceleration, which points toward the center; and the difference between real centripetal forces and fictional centrifugal forces. Equations are derived connecting position, velocity, acceleration and time. These are applied to analyze the safety of a hypothetical centrifuge ride. The goal is to give viewers an intuitive understanding of circular motion physics using real-world examples.
Takeaways
- 😳 Uniform circular motion occurs when an object moves along a circular path in a consistent way, a concept often misunderstood in Newtonian physics.
- 💨 Centripetal acceleration is the inward acceleration that occurs when an object moves in a circle, contrary to the common misconception of centrifugal force pushing outward.
- 🏓 The sensation of being pushed outward on a circular ride is due to centrifugal force, which is a fictitious force experienced from the rotating frame of reference.
- 📡 Velocity in uniform circular motion is tangential to the circle and perpendicular to the radius, illustrating the object's direction of motion at any point.
- 🤖 NASA used human centrifuges to test astronaut tolerance to acceleration, finding most could withstand 98 meters per second squared for 10 minutes.
- 💥 Centripetal force is the real force that keeps objects moving in a circle, directly influencing the circular path through centripetal acceleration.
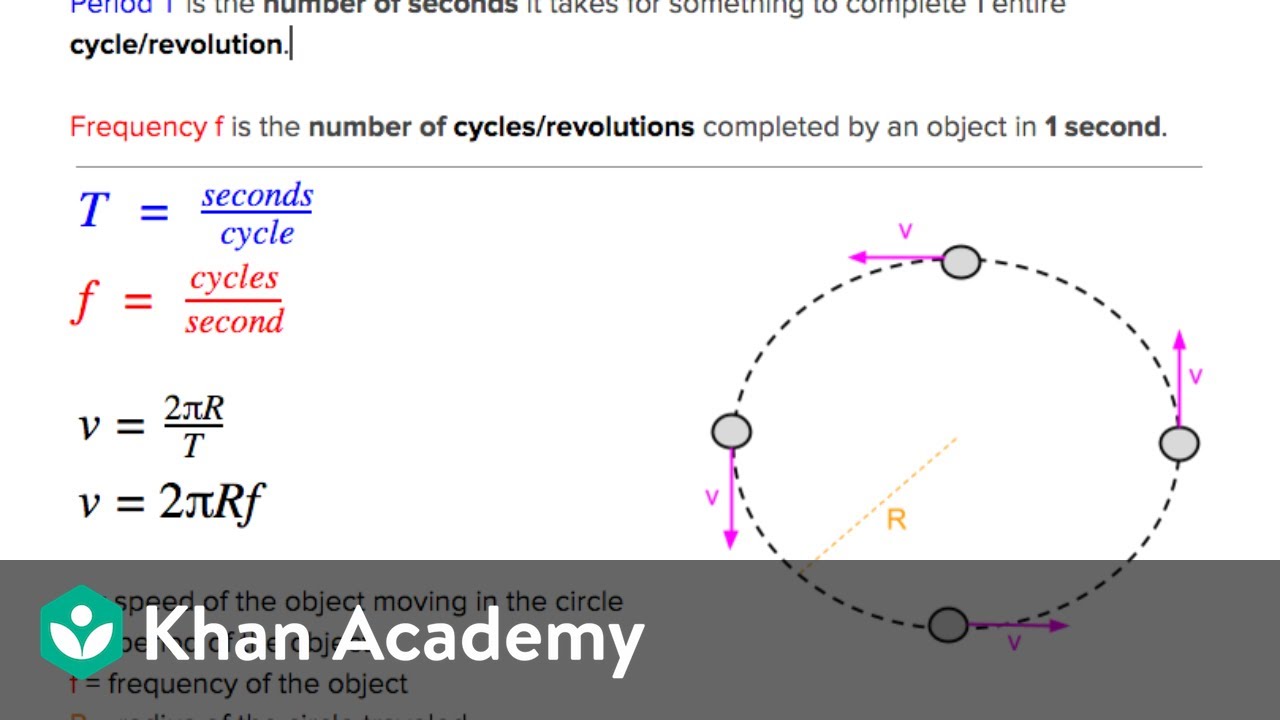
- ⏰ The period (T) of motion is the time it takes for one complete revolution, while frequency (f) is the number of revolutions per second, inversely related.
- ➡️ The speed of an object in uniform circular motion can be calculated by dividing the circumference of the path by the time period of motion.
- 📈 The magnitude of centripetal acceleration can be derived as the square of the speed divided by the radius of the circle, a key factor in understanding circular dynamics.
- 🚲 The safety of carnival rides can be assessed by calculating the centripetal acceleration experienced by riders, ensuring it's below the threshold that causes discomfort or harm.
Q & A
What is uniform circular motion?
-Uniform circular motion is when an object moves along a circular path at a consistent speed. This causes the object to experience continuous acceleration directed towards the center of the circle, known as centripetal acceleration.
What did NASA use to test how much acceleration astronauts could withstand?
-NASA used a human centrifuge, which is a powered version of a carnival ride that spins people around in a circle. They tested potential astronauts by spinning them and seeing how much acceleration they could handle before blacking out.
Why does an object moving in a circle have a velocity tangent to the circle?
-Due to inertia, an object will continue moving in a straight line unless acted on by a force. The force that causes circular motion, centripetal force, continuously changes the direction of velocity to keep the object moving in a circle. So the velocity is always tangent to the circle.
What is the difference between centripetal and centrifugal force?
-Centripetal force is the real force directed towards the center of the circle that causes circular motion. Centrifugal force is a so-called "fictitious" force that seems to push objects outwards, but actually does not exist from an external reference frame.
How can you relate period and frequency of circular motion?
-Frequency is equal to 1 divided by the period. So if it takes 2 seconds to complete one revolution (the period), the frequency is 1/2 revolutions per second.
How do you calculate the speed of circular motion?
-Take the circumference of the circle (2*pi*r) and divide it by the period. This gives you the average speed around the whole circle.
What factors affect the acceleration in circular motion?
-The acceleration is affected by the speed (velocity) and the radius - increasing speed or decreasing radius increases the acceleration.
Why did the key on a string fly off tangentially when released?
-The key had velocity tangent to the circle when held by the string. When released, there was no more force causing it to turn, so it continued moving tangentially according to its existing velocity.
Why does centrifugal force feel real from the rider's perspective?
-From the outside, the wall is pushing the rider inward. But to the rider it seems like they are being pushed outward against the wall, resulting in an apparent 'centrifugal force'.
How can you check if a spinning carnival ride is safe?
-Calculate the acceleration using the equation relating speed, radius, and acceleration. Compare the result to limits of human acceleration tolerance based on the NASA centrifuge experiments.
Outlines
🎡 Physics of Carnival Rides
This paragraph introduces the physics concept of uniform circular motion using carnival rides as an example. It explains that spinning rides create a sensation of being pushed outward, but there is actually an inward centripetal acceleration. The history of using centrifuges to test human acceleration tolerance for space travel is also discussed.
😵 Centrifugal vs Centripetal Forces
This paragraph further clarifies the difference between centrifugal and centripetal forces. Centrifugal force is explained to be fictional - it is simply a perspective change that makes the actual centripetal acceleration feel like an outward push. Equations are then derived to calculate period, frequency, velocity, and acceleration for uniform circular motion.
Mindmap
Keywords
💡uniform circular motion
💡acceleration
💡velocity
💡centripetal force
💡centrifugal force
💡period
💡frequency
💡radius
💡tangent
💡frame of reference
Highlights
Circular motion has 4 main qualities: position, velocity, acceleration, and time - all related.
Velocity direction is perpendicular to circle's radius along the tangent.
Without a force turning it, an object keeps moving tangent to its circular path.
Centripetal force and acceleration point toward the center, causing circular motion.
Centrifugal force isn't real - it's a perspective illusion caused by centripetal force.
Period is time to complete one revolution; frequency is revolutions per unit time.
Speed equation: Distance traveled / Time taken. Works for uniform circular motion.
Centripetal acceleration depends on speed and radius - directly and inversely respectively.
Faster speed or smaller radius increases centripetal acceleration felt.
Used equations to calculate safety of a sample carnival ride centrifuge.
Velocity tangent to circle; acceleration centers it. Centrifugal force not real.
Position, velocity, acceleration, time connected for uniform circular motion.
Let object go and it moves tangent to circle due to velocity direction.
Centripetal acceleration formula: v^2/r. Felt more with faster speeds or smaller circles.
Checked safe g-force range for sample carnival ride using acceleration equation.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: