8.1.1 Basics of Hypothesis Testing - The Big Picture, Null and Alternative Hypotheses

Sasha Townsend - Tulsa

7 Nov 202035:50

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the foundational concepts of hypothesis testing, outlining essential terms such as claim, hypothesis, null hypothesis, and alternative hypothesis. It aims to help viewers describe hypothesis testing, relate it to the rare event rule and sampling distributions, and identify hypotheses associated with a claim. The script uses a survey example to illustrate the process of hypothesis testing, emphasizing the importance of understanding the concepts rather than computation, and preparing viewers for further lessons on significance levels and error types.

Takeaways

📚 Hypothesis testing is a statistical method to evaluate claims about a population parameter based on sample data.
🎯 The key terms in hypothesis testing include claim hypothesis, null hypothesis, and alternative hypothesis.
🔍 The null hypothesis (H₀) assumes there is no effect or difference, and it is the statement of equality against which the test is conducted.
🚀 The alternative hypothesis (H₁) is the statement that there is an effect or difference, and it does not contain the condition of equality.
📈 Hypothesis testing involves using sample data to make inferences about the population parameter, often in the form of proportions, means, or variances.
📊 The process of hypothesis testing includes stating the claim symbolically, identifying the null and alternative hypotheses, and using the sample statistic to evaluate the null hypothesis.
📉 The rare event rule is fundamental to hypothesis testing; if an event unlikely under the null hypothesis occurs, the null hypothesis is likely incorrect.
📝 The significance of the test is determined by the p-value or critical values, which help decide whether to reject the null hypothesis based on the sample statistic's extremity.
🤖 Technology, such as Excel, is used to assist in hypothesis testing by calculating probabilities, z-scores, and p-values, but the focus is on understanding the concepts rather than computation.
📉 A sampling distribution is used to visualize the distribution of a sample statistic assuming the null hypothesis is true, helping to determine if the observed sample statistic is extreme.
📝 The conclusion of a hypothesis test should be stated in non-technical terms to make the findings accessible to a broader audience.

Q & A

What is the main focus of lesson 8.1 in the video?
-Lesson 8.1 focuses on the big picture of hypothesis testing, including defining essential terms such as claim hypothesis, null hypothesis, and alternative hypothesis, and understanding how to describe hypothesis testing in one's own words.
What are the two main goals the instructor has for the students by the end of the video?
-The two main goals are for students to be able to describe hypothesis testing in their own words, understand its relation to the rare event rule and sampling distributions, and to be able to identify the null and alternative hypotheses associated with a given claim.
What is a hypothesis in statistical terms?
-In statistics, a hypothesis is a claim or statement about a property of a population, such as a population proportion, mean, standard deviation, or variance.
What is the difference between a null hypothesis and an alternative hypothesis?
-The null hypothesis (denoted as H0) is a statement that the value of a population parameter is equal to some claimed value. The alternative hypothesis (denoted as H1 or Ha) is a statement that the parameter has a value that differs from the value in the null hypothesis.
How does the instructor suggest identifying the null and alternative hypotheses for a given problem?
-The instructor suggests stating the claim in symbolic form, considering what would have to be true if the claim isn't true, and then identifying the statement without the condition of equality as the alternative hypothesis. The null hypothesis is then formed by changing the inequality sign to an equal sign in the alternative hypothesis.
What is the rare event rule, and how does it relate to hypothesis testing?
-The rare event rule states that if under a given assumption, the probability of a particular observed event is very small and the event occurs significantly less or more often than expected, then the assumption is probably not correct. In hypothesis testing, this rule is used to decide whether to reject the null hypothesis based on the observed sample statistic.
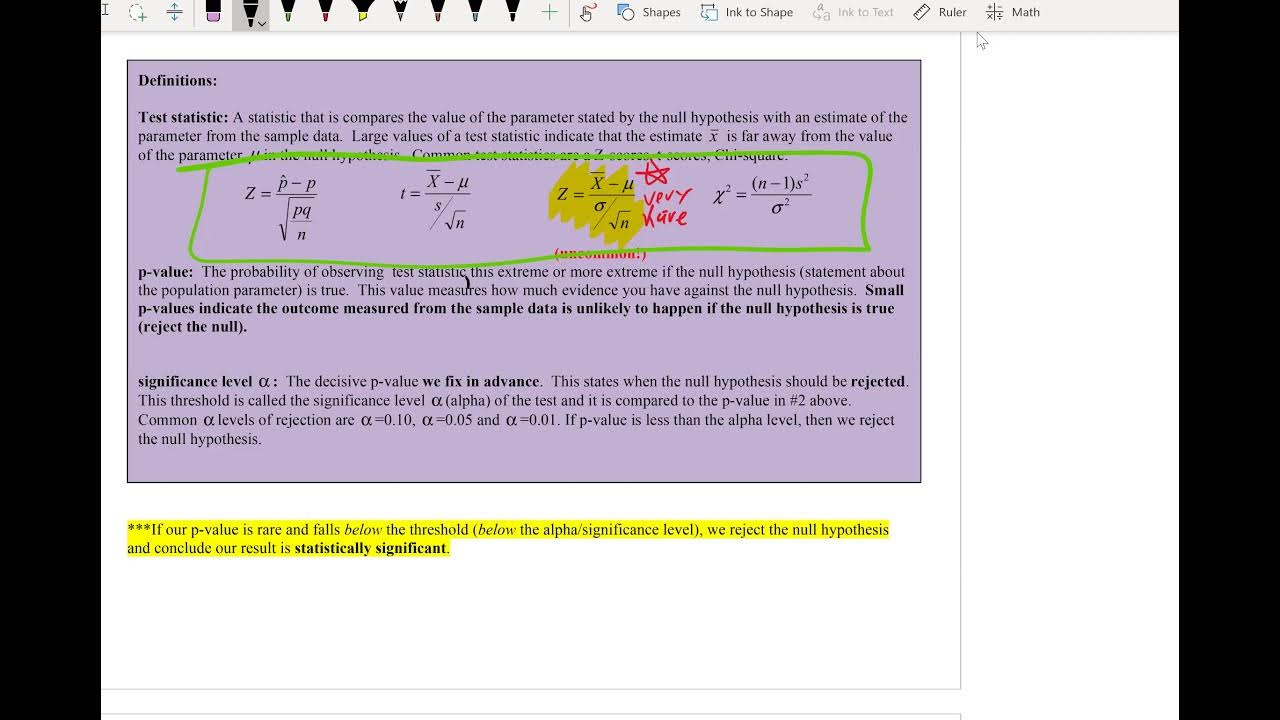
What is the purpose of computing the test statistic in hypothesis testing?
-The test statistic, which could be a z-score, t-score, or chi-squared score, is used to determine how many standard deviations the sample statistic is from the mean under the assumption that the null hypothesis is true. This helps in assessing whether the observed sample statistic is extreme enough to reject the null hypothesis.
What are the two methods mentioned in the video for making a decision about the null hypothesis?
-The two methods mentioned are the critical value method and the p-value method. Both methods involve comparing the test statistic to certain thresholds to determine if the null hypothesis should be rejected.
Why is it important to state the conclusion of a hypothesis test in non-technical terms?
-Stating the conclusion in non-technical terms makes the results of the hypothesis test understandable to a broader audience, including those who may not have a background in statistics.
What is the significance of the sample size in hypothesis testing?
-The sample size is important because it is a characteristic of the sampling distribution that affects the shape and standard deviation of that distribution. It plays a crucial role in determining the test statistic and the validity of the hypothesis test.
How does the instructor emphasize the importance of understanding the concepts in statistics over computation?
-The instructor emphasizes that while computation is necessary, the focus in a statistics class should be on understanding the concepts and the reasoning behind each step. This understanding is crucial for interpreting the results and knowing what the computed values mean in the context of the hypothesis test.

Outlines

00:00

📊 Introduction to Hypothesis Testing

This video lesson covers the fundamental concepts of hypothesis testing. It defines key terms such as claim, hypothesis, null hypothesis, and alternative hypothesis. The goal is for viewers to understand hypothesis testing and its relation to the rare event rule and sampling distributions. Although the video doesn't cover conducting a hypothesis test, it lays the groundwork for understanding the process and its connection to previous lessons on sampling distributions and confidence intervals.

05:00

🔢 Formulating Hypotheses

The video discusses the process of formulating null and alternative hypotheses from a given claim. The null hypothesis (H0) states that a population parameter is equal to a claimed value, while the alternative hypothesis (H1) suggests the parameter differs from the claimed value. The lesson emphasizes identifying and writing these hypotheses correctly and explains their importance in hypothesis testing.

10:01

📈 Testing Hypotheses: An Example

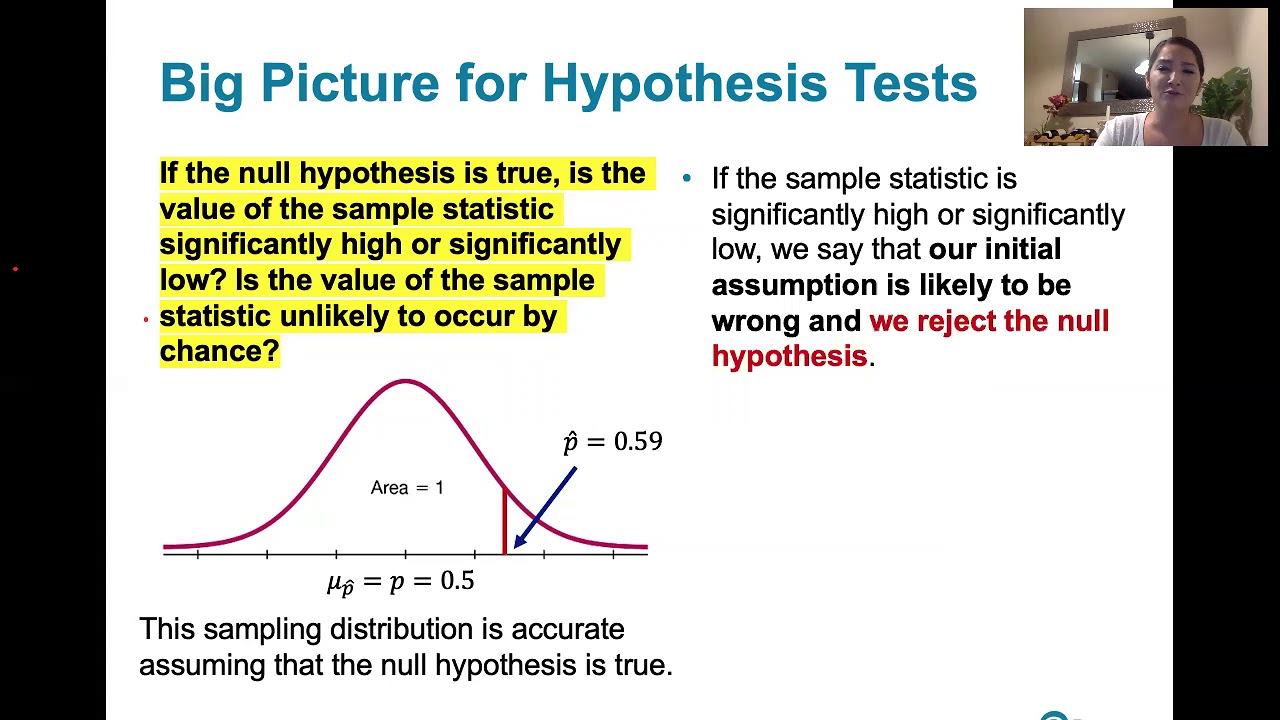
Using a practical example, the video demonstrates how to test hypotheses by calculating sample statistics and understanding their significance. It explains the role of sample size and sample proportion in forming sampling distributions. The example involves determining if 59% of a sample indicates a true population proportion greater than 50%, illustrating the steps in hypothesis testing and the importance of understanding sampling distributions.

15:02

🔍 Applying the Rare Event Rule

This segment delves into applying the rare event rule in hypothesis testing. It explains how to determine if an observed sample statistic is extreme under the null hypothesis. If an event is rare but occurs, the assumption (null hypothesis) might be incorrect. This principle underpins hypothesis testing, where rare outcomes suggest rejecting the null hypothesis.

20:04

📊 Steps in Hypothesis Testing

The video outlines the procedural steps in hypothesis testing. Starting with stating the claim in symbolic form, it proceeds to inferring the null and alternative hypotheses, identifying sample statistics, and using sampling distributions to test the hypotheses. The example revisits the claim that 59% of a sample would erase personal information online, assessing if this supports rejecting the null hypothesis.

25:04

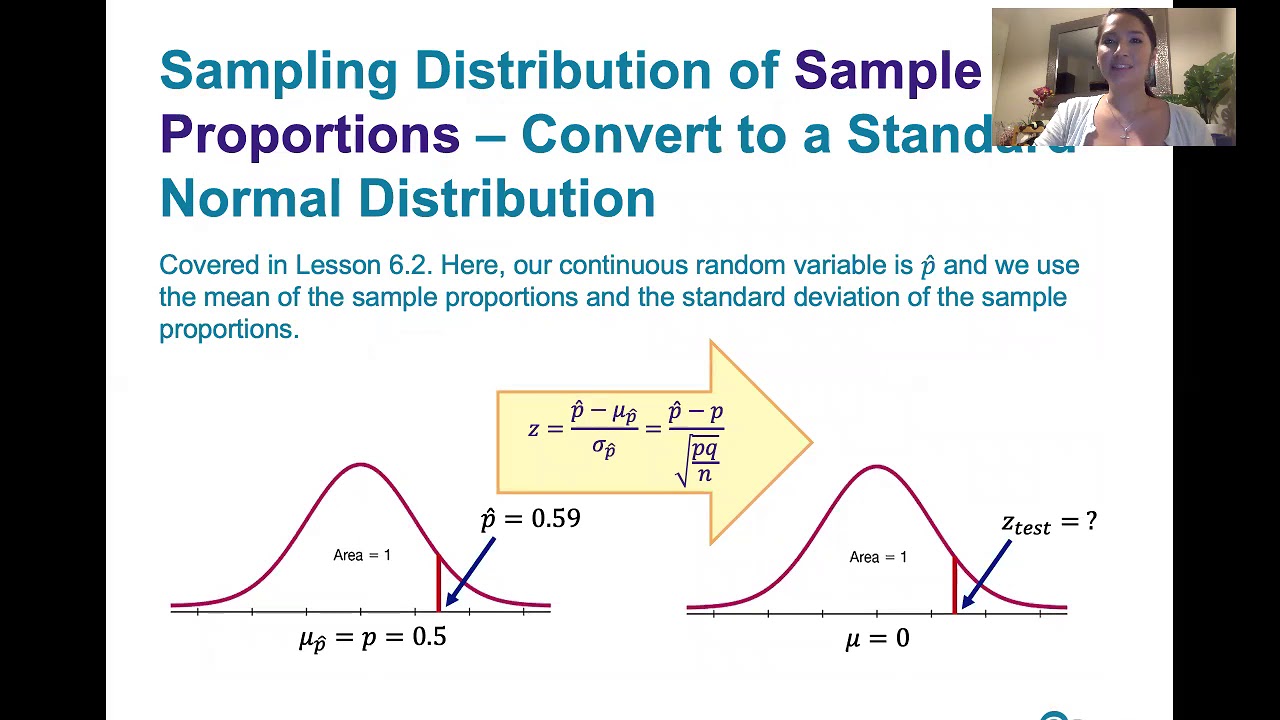
🧮 Calculating Test Statistics

This part focuses on computing test statistics like z-scores, t-scores, and chi-squared statistics from sample data. It explains converting sample statistics into standardized forms to determine their significance. The video emphasizes understanding the statistical output and its implications for the original hypothesis.

30:05

📊 Using Technology in Hypothesis Testing

The video discusses utilizing tools like Excel, statistical formulas, and tables for hypothesis testing. It underscores that the focus should be on understanding concepts rather than just computation. The goal is to interpret statistical outputs, like z-scores and p-values, and understand their meaning concerning the hypothesis.

35:07

📋 Conclusion and Example on Drone Delivery

The video wraps up by reinforcing the hypothesis testing procedure. It revisits writing claims in symbolic form, formulating null and alternative hypotheses, and computing sample statistics. An additional example involving consumer comfort with drone delivery is used to practice these steps, ensuring a comprehensive understanding of the process.

Mindmap

Keywords

💡Hypothesis Testing

Hypothesis testing is a statistical method used to make decisions about a population parameter based on a sample. It's the core process discussed in the video, involving the examination of claims or statements about a population. The video script introduces hypothesis testing as a way to determine if a sample provides enough evidence to support or reject a claim, using the rare event rule and sampling distributions as foundational concepts.

💡Claim Hypothesis

A claim hypothesis, in the context of the video, is a statement or belief about a property of a population that is being tested. It is often the initial assumption or belief that most people hold about a certain condition. For example, the claim hypothesis in the script is that 'most adults would erase all of their personal online information if they could,' which is then translated into a symbolic form for testing.

💡Null Hypothesis

The null hypothesis, denoted as H0, is a statement of no effect or no difference in statistical testing. It is used as a baseline for comparison against the alternative hypothesis. In the video, the null hypothesis is the assumption that the proportion of adults who would erase their online information is equal to 0.5, which is then tested against the claim hypothesis.

💡Alternative Hypothesis

The alternative hypothesis, represented as Ha, is a statement that contradicts the null hypothesis and proposes a different outcome or effect. It is what researchers believe to be true if the null hypothesis is not supported by the data. In the script, the alternative hypothesis is that the proportion of adults wanting to erase their online information is greater than 0.5.

💡Rare Event Rule

The rare event rule is a principle in statistics that if an event with a low probability of occurring under a given assumption does occur, then the assumption is likely incorrect. The video explains that this rule is fundamental to hypothesis testing, as it guides the decision to reject the null hypothesis when the sample statistic is an unlikely outcome given the null hypothesis.

💡Sampling Distributions

Sampling distributions are the probability distributions of a given statistic based on a random sample. They provide a range of possible outcomes and their associated probabilities, which are essential for hypothesis testing. The video script discusses how sampling distributions, along with the rare event rule, helps in understanding the likelihood of the observed sample statistic under the null hypothesis.

💡Significance Level

The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. It represents the threshold for deciding when the evidence against the null hypothesis is strong enough. Although not explicitly defined in the script, the concept is alluded to when discussing the probability of rare events and the decision to reject the null hypothesis.

💡Type 1 and Type 2 Errors

Type 1 error is the incorrect rejection of a true null hypothesis, while Type 2 error is incorrectly failing to reject a false null hypothesis. These concepts are crucial for understanding the implications of hypothesis testing decisions. The script mentions these error types in the context of the next video, indicating their importance in hypothesis testing.

💡Test Statistic

A test statistic is a standardized value that measures how far the sample statistic is from the hypothesized population parameter. It is used to determine the probability of observing the sample statistic under the null hypothesis. The script explains that the test statistic, such as a z-score, is used to assess the rarity of the observed sample statistic in relation to the null hypothesis.

💡P-Value

The p-value is the probability of observing a sample statistic as extreme or more extreme than the one observed, assuming the null hypothesis is true. It is used to make a decision about the null hypothesis. The script mentions the p-value method as one of the approaches to hypothesis testing, indicating its role in evaluating the evidence against the null hypothesis.

💡Critical Value

A critical value is a threshold value used in hypothesis testing to determine whether to reject the null hypothesis. If the test statistic falls beyond the critical value, the null hypothesis is rejected. The script discusses the critical value method as an alternative to the p-value method for making decisions about the null hypothesis based on the test statistic.

Highlights

Lesson 8.1 introduces hypothesis testing, focusing on defining key terms such as claim hypothesis, null hypothesis, and alternative hypothesis.

The goal is to understand hypothesis testing in relation to the rare event rule and sampling distributions.

Hypothesis testing, also known as a test of significance, is a formal procedure for testing claims about population properties.

The video discusses the importance of understanding confidence intervals and sampling distributions in hypothesis testing.

An example involving personal online data is presented to illustrate the concept of hypothesis testing.

The symbolic form of a claim is explained, demonstrating how to translate a verbal claim into a statistical hypothesis.

The process of identifying null and alternative hypotheses from a claim is detailed step by step.

The null hypothesis (H0) is defined as a statement of equality to a claimed value, while the alternative hypothesis (Ha) indicates inequality.

A step-by-step guide is provided to identify the null and alternative hypotheses for a given problem.

The significance of the sample statistic and its role in hypothesis testing is explained using an example.

The concept of the rare event rule is applied to hypothesis testing, explaining when to reject the null hypothesis.

The procedure for hypothesis testing includes stating the claim symbolically, identifying hypotheses, and evaluating sample statistics.

The importance of understanding the meaning behind statistical outputs such as z-scores and p-values is emphasized.

The video outlines the two methods for making decisions about the null hypothesis: the critical value method and the p-value method.

The final step in hypothesis testing is to state the conclusion in non-technical terms for clarity and accessibility.

The focus of learning in statistics is on understanding concepts rather than computation, which is facilitated by technology.

The video concludes with an example involving drone delivery to practice writing claims symbolically and identifying hypotheses.

The procedure for hypothesis testing is summarized in a step-by-step outline, providing a clear method for students to follow.

Transcripts

Browse More Related Video

8.1.2 Basics of Hypothesis Testing - Significance Level, Type I and Type II Error

8.2.1 Testing a Claim About a Proportion - P-value, Critical Value Methods, Normal Approximation

Permutation Hypothesis Testing with Example | Statistics Tutorial # 37 | MarinStatsLectures

8.1.3 Basics of Hypothesis Testing - Computing and Interpreting Test Statistics

Intro to Hypothesis Testing in Statistics - Hypothesis Testing Statistics Problems & Examples

Math 119 Chap 8 part 1

Related Tags

Hypothesis Testing Null Hypothesis Alternative Hypothesis Statistical Analysis Sampling Distribution Rare Event Rule Data Privacy Drone Delivery Online Surveys Significance Level