Ch 12: What are generators in classical mechanics? | Maths of Quantum Mechanics

Quantum Sense
31 Jan 202314:17
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the concept of generators in classical physics and their significance in understanding the Lagrangian framework. It contrasts the quantum state's unified nature with the fragmented approach of Newtonian mechanics, highlighting the elegance of the Lagrangian function that encapsulates a particle's classical state. The script explains the derivation of the Euler-Lagrange equation and its connection to Newton's second law, and further explores how changes in the Lagrangian are linked to momentum, energy, and angular momentum, hinting at their quantum mechanical counterparts. The episode sets the stage for deriving the Schrödinger equation and provides insights into the quantum world through the lens of classical physics.

Takeaways
  • 📚 The episode focuses on generators in classical physics and their fundamental role in deriving the Schrödinger equation.
  • 🌟 Quantum mechanics simplifies the understanding of a particle's state with a single object - the quantum state, unlike Newtonian mechanics which uses multiple variables.
  • 📈 The Lagrangian framework is introduced as a way to find patterns in classical physics and as a precursor to quantum mechanics.
  • 🔄 The Lagrangian is a function of time, position, and velocity, and is central to classical physics, similar to how the quantum state is central to quantum physics.
  • 🌐 The choice of Lagrangian as kinetic energy minus potential energy will be derived from quantum mechanics in a later episode.
  • 🎯 The principle of stationary action, not just least action, is used to determine the correct path of a particle in the Lagrangian framework.
  • 📊 The Euler-Lagrange equation is a key tool for finding the function of time that stationarizes the action integral and is a more abstract version of Newton's second law.
  • 🔄 The Lagrangian framework reveals patterns where changes in momentum are connected to changes in position, and vice versa.
  • ⏳ Time variations in the Lagrangian are related to changes in energy, hinting at the generator of time change in classical mechanics.
  • 🌐 The concept of generators in classical physics is foundational for understanding quantum mechanics, where operators like momentum and position are expected to generate changes in position and momentum.
  • 🚀 The episode teases insights into how classical physics concepts will be fully explored in the context of quantum mechanics in upcoming episodes.
Q & A

  • What is the main focus of this episode?

    -The main focus of this episode is to discuss and derive generators in classical physics, particularly within the Lagrangian framework, and to introduce how these concepts will be fundamental to understanding the Schrodinger equation in the next episode.

  • What is the quantum state in quantum mechanics?

    -The quantum state is a mathematical object in quantum mechanics that holds all the information about a particle, including its possible positions, momenta, energies, and their probabilities.

  • How does the Lagrangian function relate to the classical state of a particle?

    -The Lagrangian function is a function of time, position, and velocity that represents the classical state of a particle, analogous to the quantum state in quantum mechanics, and it helps to see the bigger picture and patterns in physics.

  • What is the assumed form of the Lagrangian?

    -The assumed form of the Lagrangian is kinetic energy minus potential energy, denoted as L = T - V, where T is the kinetic energy and V is the potential energy.

  • What is the principle of stationary action?

    -The principle of stationary action states that the correct path of a particle is the one that forms a stationary point of the action integral, which can be a minimum, maximum, or a saddle point.

  • How does the Euler-Lagrange equation relate to Newton's second law?

    -The Euler-Lagrange equation, when the Lagrangian is assumed to be the kinetic energy minus the potential energy, results in the equation that is equivalent to Newton's second law, relating the force to the mass and acceleration of the particle.

  • What does the Euler-Lagrange equation imply about momentum and position?

    -The Euler-Lagrange equation implies that changes in momentum are intimately connected to changes in the position of the particle's state, and vice versa.

  • How does the Lagrangian framework help reveal patterns in physics?

    -The Lagrangian framework helps reveal patterns in physics by showing how changes in various physical quantities (like momentum, position, energy, and angular momentum) are related to each other through the variation of the Lagrangian with respect to different parameters.

  • What is the role of energy in the Lagrangian framework?

    -In the Lagrangian framework, changes in energy are intimately related to changes in the time of the particle's state, suggesting that energy generates time changes in the system.

  • How does the concept of generators in classical physics relate to quantum mechanics?

    -The concept of generators in classical physics, where physical quantities generate changes in the state of a particle, has a direct analogy in quantum mechanics. For example, momentum generates spatial changes, and this idea will be used to understand how quantum states evolve in time.

  • What is the significance of angular momentum in the Lagrangian framework?

    -In the Lagrangian framework, changes in angular momentum are related to changes in the rotation of the particle's state, and this relationship holds true even in angular coordinates, showing another pattern in the physics of the system.

Outlines
00:00
📚 Introduction to Classical Generators and Lagrangian Mechanics

This paragraph introduces the concept of generators in classical physics and their significance in understanding the Schrodinger equation. The speaker aims to provide a brief overview of Lagrangian physics, emphasizing its role in revealing fundamental patterns in physics that are not apparent in Newtonian mechanics. The quantum state's unified nature is contrasted with the individual dynamical variables in Newtonian mechanics, highlighting the need for a central object in classical physics akin to the quantum state. The Lagrangian is introduced as this central function, representing the classical state of a particle and depending on time, position, and velocity. The speaker mentions two key facts about the Lagrangian that will be derived from quantum mechanics in a later episode: the form of the Lagrangian (kinetic energy minus potential energy) and the principle of stationary action, which determines the particle's path.

05:04
🔍 Deriving the Euler-Lagrange Equation and its Implications

The paragraph delves into the process of finding the function of time that stationarizes the action integral, which is directed towards the Euler-Lagrange equation. The speaker mentions the need for a course on the calculus of variations to understand this derivation but assures that the assumed form of the Lagrangian leads to Newton's second law in a more abstract form. The Euler-Lagrange equation is then examined to reveal patterns in classical mechanics, showing that changes in momentum are connected to changes in position and vice versa. The paragraph also explores the relationship between the Lagrangian's variation with respect to momentum and position, and how these variations relate to changes in physical quantities over time.

10:06
🌟 Unveiling the Pattern in Classical Generators

This paragraph synthesizes the discussion on classical generators and their role in the Lagrangian framework. The speaker presents a series of equations that follow a common pattern, indicating that changes in the Lagrangian due to variations in certain parameters are equivalent to observing changes in specific physical quantities over time. The paragraph establishes that momentum generates spatial change, position generates momentum change, energy generates time change, and angular momentum generates rotational change. The relevance of these classical findings to quantum mechanics is highlighted, suggesting that the Lagrangian framework provides insights into the quantum world. The speaker also teases future discussions on how quantum operators like momentum and position relate to changes in position and momentum, respectively.

Mindmap
Keywords
💡Quantum State
The quantum state is a fundamental concept in quantum mechanics that encapsulates all the possible information about a particle, such as its position, momentum, energy, and their associated probabilities. It is a mathematical object that contrasts with the separate dynamical variables used in Newtonian mechanics. In the context of the video, the quantum state is presented as a unified entity that simplifies the understanding of a particle's properties compared to the individual variables in classical physics.
💡Lagrangian Framework
The Lagrangian framework is a classical mechanics approach that uses a function called the Lagrangian to describe the motion of a system. The Lagrangian is a function of time, position, and velocity, and it allows for the derivation of the system's equations of motion through the principle of stationary action. This framework is significant in the video as it sets the stage for understanding how classical mechanics can be related to quantum mechanics, and it is used to derive the Euler-Lagrange equation, which is analogous to Newton's second law.
💡Schrodinger Equation
The Schrödinger equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is derived in the video's follow-up episode and is mentioned as a key goal of the discussion on generators in classical physics. The equation is crucial for understanding quantum systems and predicting their behavior.
💡Generators
In the context of the video, generators are physical quantities that produce changes in the state of a system. They are related to how the Lagrangian varies when certain parameters are changed. For instance, momentum is the generator of spatial change, and energy is the generator of time change. The concept of generators is used to draw parallels between classical and quantum mechanics, where operators in quantum mechanics generate changes in state similar to how physical quantities generate changes in classical mechanics.
💡Euler-Lagrange Equation
The Euler-Lagrange equation is a differential equation that arises in the Lagrangian framework of classical mechanics. It provides a way to find the function of time that stationarizes the action integral, which in turn gives the correct path of a particle. The equation is derived from the principle of stationary action and is equivalent to Newton's second law in a more abstract form, relating the spatial derivative of the potential energy to the time derivative of mass times velocity (which is acceleration).
💡Action Integral
The action integral is a quantity in classical mechanics that is used to determine the path taken by a particle over time. It is an integral involving the Lagrangian, and the principle of stationary action states that the actual path taken by a particle is the one for which the action integral is stationary. This concept is central to the Lagrangian framework and is used to derive the equations of motion for a system.
💡Quantum Path Integral
The quantum path integral is a concept in quantum mechanics that involves summing over all possible paths a particle can take between two points. It is used to calculate the probability amplitude for a particle to go from one point to another and is related to the concept of generators in classical mechanics. The quantum path integral is mentioned in the video as a way to derive the form of the Lagrangian from quantum mechanics.
💡Newtonian Mechanics
Newtonian mechanics, also known as classical mechanics, is a framework that describes the motion of objects using Newton's laws of motion and the concept of forces. It is contrasted with quantum mechanics in the video, where the quantum state is seen as a more unified and simplified representation of a particle's properties compared to the individual dynamical variables used in Newtonian mechanics.
💡Classical State
In the context of the video, the classical state refers to the description of a particle's motion using classical mechanics, specifically through the Lagrangian framework. It is analogous to the quantum state in quantum mechanics, as both aim to provide a comprehensive description of a particle's properties. The classical state, represented by the Lagrangian, encapsulates information about the particle's position, velocity, and time.
💡Momentum
Momentum in physics is the product of an object's mass and its velocity. It is a key concept in both classical and quantum mechanics. In the video, momentum is described as the generator of spatial change, meaning that changes in momentum are related to changes in the position of a particle. This relationship is highlighted through the Euler-Lagrange equation in the Lagrangian framework.
💡Energy
Energy in physics is the capacity to do work or the cause of motion. In the context of the video, energy is described as the generator of time change, meaning that changes in the energy of a system are related to changes in time within the system's state. This concept is used to draw parallels between classical mechanics and quantum mechanics, where the energy operator is expected to generate time evolution in quantum states.
Highlights

The introduction of generators in classical physics as a fundamental concept for understanding the Schrodinger equation.

The Lagrangian framework is introduced as a way to derive Lagrangian physics from quantum mechanics.

A brief overview of Lagrangian physics is provided to set the scene for understanding generators in classical physics.

Quantum mechanics simplifies the understanding of particle information with the quantum state, unlike Newtonian mechanics.

The Lagrangian is presented as a central function in classical physics, analogous to the quantum state, representing the classical state of a particle.

The Lagrangian is defined as a function of time, position, and velocity, and is typically the difference between kinetic and potential energy.

The principle of stationary action is explained, which involves finding the path of a particle that minimizes or maximizes the action integral.

The Euler-Lagrange equation is derived, which is a fundamental differential equation in the Lagrangian framework and relates to Newton's second law.

The Euler-Lagrange equation shows a profound connection between changes in momentum and changes in position.

The Lagrangian framework reveals patterns in physics that are hidden in Newtonian mechanics, such as the relationship between position, momentum, energy, and angular momentum.

The concept of generators in classical physics is introduced, where physical quantities like momentum, position, energy, and angular momentum generate changes in the state of a particle.

The Lagrangian framework is essential for understanding the bigger picture in physics and is relevant to quantum mechanics.

The potential connection between classical and quantum mechanics is hinted at, suggesting that classical concepts may have quantum counterparts.

The anticipation of future episodes where the Schrodinger equation will be derived and quantum concepts will be explored in more depth.

The potential quantum insights from classical physics, such as the expectation that the momentum operator in quantum mechanics should cause a change in position.

The episode concludes with an encouragement for viewers to stay tuned for the next episode, where the Schrodinger equation will be derived.

Transcripts

Browse More Related Video

Lagrangian and Hamiltonian Mechanics in Under 20 Minutes: Physics Mini Lesson

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation

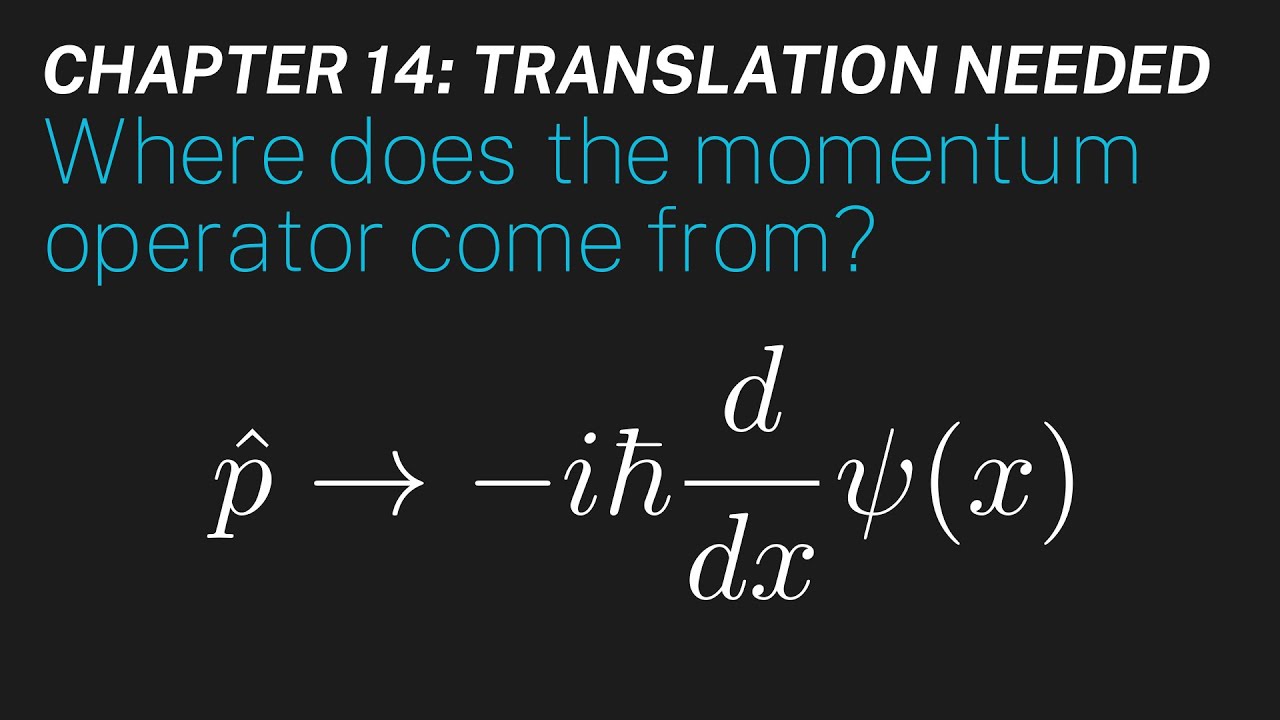
Ch 14: Where does the momentum operator come from? | Maths of Quantum Mechanics

Classical Mechanics | Lecture 6

Lecture 10 | The Theoretical Minimum

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (4 of 92) The Schrodinger Eqn. "Derived"

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsClassicalPhysicsSchrodingerEquationLagrangianMechanicsPathIntegralEulerLagrangeEnergyMomentumPhysicsDerivationEducationalContent