Calculus AB/BC – 1.8 Determining Limits Using the Squeeze Theorem

The Algebros
27 Sept 202011:45
EducationalLearning
32 Likes 10 Comments

TLDRIn this calculus lesson, Mr. Bean introduces the Squeeze Theorem, also known as the Sandwich Theorem, explaining its concept and application in finding limits. He demonstrates the theorem with the example of the function \( x^2 \cos(\frac{1}{x^2}) \), showing how to determine the limit as \( x \) approaches zero without direct substitution. The lesson also includes practice problems to solidify understanding, emphasizing the importance of the theorem's conditions, such as bounded functions, for successful application.

Takeaways
  • 📚 The Squeeze Theorem, also known as the Sandwich Theorem or Pinching Theorem, helps determine limits by squeezing a function between two others.
  • 📊 If a function f(x) is squeezed between two functions g(x) and h(x), and the limits of g(x) and h(x) as x approaches a are the same, then the limit of f(x) as x approaches a is the same as well.
  • 🔍 An example is given with the limit as x approaches 0 of x^2 * cos(1/x^2). Since cosine oscillates between -1 and 1, multiplying by x^2 gives bounds of -x^2 and x^2.
  • 🧮 By the Squeeze Theorem, since the limits of -x^2 and x^2 as x approaches 0 are both 0, the limit of x^2 * cos(1/x^2) as x approaches 0 is also 0.
  • 🔢 Another example involves finding the limit of a function f(x) without explicitly knowing f(x), but knowing it is squeezed between g(x) and h(x) as x approaches 2.
  • 💡 The Squeeze Theorem is particularly useful in cases where direct substitution in a limit leads to indeterminate forms.
  • 🚫 The Squeeze Theorem cannot determine the exact limit if the bounding functions have different limits at the point of interest.
  • 🔍 For certain intervals, functions might be squeezed between others only within those intervals, which is important for applying the theorem.
  • 🧮 The Squeeze Theorem fails if one of the bounding functions exhibits unbounded behavior, such as having a vertical asymptote.
  • ✅ Using the Squeeze Theorem involves checking the limits of the bounding functions and ensuring they are equal to conclude the limit of the squeezed function.
Q & A

  • What is the Squeeze Theorem also known as?

    -The Squeeze Theorem is also known as the Sandwich Theorem or Pinching Theorem.

  • What does the Squeeze Theorem state in terms of functions?

    -The Squeeze Theorem states that if a function 'f' is squeezed between two other functions 'g' and 'h', and the limits of 'g' and 'h' as x approaches a certain value are the same, then the limit of 'f' as x approaches that value is also the same as the limits of 'g' and 'h'.

  • How does the Squeeze Theorem apply to the function f(x) = x^2 * cos(1/x^2) as x approaches 0?

    -The Squeeze Theorem applies by recognizing that cos(1/x^2) is bounded between -1 and 1. By multiplying these bounds by x^2, we can determine that the limit of f(x) as x approaches 0 is 0, since x^2 * -1 and x^2 * 1 both approach 0.

  • What is the range of the cosine function?

    -The range of the cosine function is between -1 and 1, inclusive.

  • Why can't direct substitution be used for the limit of x^2 * cos(1/x^2) as x approaches 0?

    -Direct substitution cannot be used because plugging in 0 for x results in division by zero, which is undefined.

  • What is the main idea behind the example problem involving g(x) and h(x) where x approaches 2?

    -The main idea is to determine if the Squeeze Theorem can be used to find the limit of an unknown function 'f' given the limits of 'g' and 'h' as x approaches 2. If the limits of 'g' and 'h' are the same, then 'f' is squeezed between them, but without the actual function 'f', the exact limit cannot be determined.

  • What is the significance of the notation 'from negative one to five' in the context of the Squeeze Theorem?

    -The notation 'from negative one to five' signifies the interval during which the inequality g < f < h holds true. It does not directly affect the calculations but helps to understand when the Squeeze Theorem can be applied.

  • Why can't the Squeeze Theorem be used if the boundary functions are unbounded?

    -The Squeeze Theorem cannot be used with unbounded functions because the theorem relies on the limits of the boundary functions being the same finite value, which is not the case with unbounded functions.

  • How does the Squeeze Theorem help in determining the limit of a function if the limits of the boundary functions are the same?

    -If the limits of the boundary functions are the same, the Squeeze Theorem allows us to conclude that the limit of the function in between them is also the same, providing a way to find the limit without knowing the exact form of the function.

  • What is the condition for the Squeeze Theorem to be applicable to a set of functions?

    -The Squeeze Theorem is applicable if there are three functions where the lower function is less than or equal to the middle function, which in turn is less than or equal to the upper function, and the limits of the lower and upper functions as x approaches a certain value are equal.

Outlines
00:00
📚 Introduction to the Squeeze Theorem

Mr. Bean introduces the Squeeze Theorem, also known as the Sandwich Theorem, explaining its concept and practical application. The theorem is used to find the limit of a function 'f' that is 'sandwiched' between two other functions 'g' and 'h'. If both 'g' and 'h' approach the same limit 'l' as 'x' approaches a certain value 'a', then 'f' must also approach 'l'. An example is given where the limit of 'x^2 * cos(1/x^2)' as 'x' approaches 0 is found using the Squeeze Theorem, despite direct substitution being undefined.

05:01
🔍 Applying the Squeeze Theorem in Practice

The script continues with practical examples of the Squeeze Theorem, illustrating how to determine limits when direct substitution is not possible. It explains that if functions 'g' and 'h' are given with 'g < f < h' and their limits as 'x' approaches a certain value are known, the limit of 'f' must lie between them. However, without knowing the exact function 'f', only an interval for its limit can be determined. The importance of understanding when the Squeeze Theorem is applicable is emphasized, noting that it cannot be used if the boundary functions are unbounded.

10:01
🚫 Limitations of the Squeeze Theorem

The final part of the script discusses the limitations of the Squeeze Theorem, specifically highlighting that it cannot be applied when the boundary functions exhibit unbounded behavior, such as '1/x' approaching zero. Unbounded functions create vertical asymptotes and do not have a limit, thus disqualifying their use in the theorem. The script concludes with a reminder to be cautious of unbounded behavior when applying the Squeeze Theorem and encourages students to practice and master the concept.

Mindmap
Keywords
💡Squeeze Theorem
The Squeeze Theorem, also known as the Sandwich Theorem or Pinching Theorem, is a fundamental concept in calculus that allows for the determination of a limit when direct substitution is not possible. The theorem states that if two functions, g and h, 'squeeze' a third function f between them as x approaches a certain value, and the limits of g and h are the same, then the limit of f must also be that value. In the video, Mr. Bean uses the Squeeze Theorem to find the limit of a function as x approaches zero, where direct substitution would result in an undefined expression.
💡Limit
In calculus, a limit is the value that a function or sequence 'approaches' as the input or index approaches some value. The concept is central to understanding continuity and differentiability. In the context of the video, the limit is used to find the value that a function approaches as x approaches a specific point, such as zero. The script discusses how the Squeeze Theorem can be used to determine limits when direct substitution is not feasible.
💡Direct Substitution
Direct substitution is a method in calculus where you substitute the value you're taking the limit of directly into the function to find the limit. However, this method is not always applicable, especially when it results in an undefined expression, such as division by zero. In the script, direct substitution is mentioned as an approach that cannot be used for the given function due to the cosine term, leading to the application of the Squeeze Theorem instead.
💡Cosine Function
The cosine function is a trigonometric function that describes a wave with a period of 2π, oscillating between -1 and 1. It is used in various mathematical and real-world applications, including physics and engineering. In the video, the cosine function is part of the expression for which the limit is being sought, and its bounded nature between -1 and 1 is crucial for applying the Squeeze Theorem.
💡Graph
In the context of the video, a graph represents the visual plot of a function, showing the relationship between the input (x-values) and the output (y-values). The script uses graphs to illustrate the concept of the Squeeze Theorem, showing how the function f is 'squeezed' between the graphs of g and h. The visual representation helps in understanding how the theorem can be applied to determine limits.
💡Unbounded Behavior
Unbounded behavior in a function refers to a situation where the function's values increase or decrease without limit as the input approaches a certain value. For example, the function 1/x approaches infinity as x approaches zero. In the video, Mr. Bean warns that the Squeeze Theorem cannot be applied if one of the boundary functions exhibits unbounded behavior, as it does not allow for a finite limit to be determined.
💡AP Exam
The AP Exam, or Advanced Placement Exam, is a standardized test in the United States for high school students to earn college credit or advanced placement. The script mentions that the problems presented are the types of problems one might encounter on an AP Exam, indicating the level of difficulty and the relevance of the Squeeze Theorem in advanced high school calculus.
💡Practice Problem
A practice problem is an exercise designed to help learners apply and reinforce their understanding of a concept. In the video, Mr. Bean provides practice problems involving the Squeeze Theorem to help students understand how to apply the theorem in various contexts and to determine limits of functions.
💡Vertical Asymptote
A vertical asymptote is a value of x for which a function is undefined, typically because the function approaches infinity or negative infinity. In the script, Mr. Bean uses the example of the function 1/x to illustrate a vertical asymptote at x=0, which is a situation where the Squeeze Theorem cannot be applied due to the unbounded behavior of the function.
💡Mastery Check
A mastery check is an assessment or set of problems used to evaluate a student's understanding of a particular topic. In the video, Mr. Bean encourages students to apply what they've learned about the Squeeze Theorem in a mastery check, which is a way to test their ability to use the theorem to solve problems.
Highlights

Introduction to the Squeeze Theorem, also known as the Sandwich Theorem or Pinching Theorem.

Explanation of the Squeeze Theorem's concept where a function f is trapped between two other functions g and h.

Graphical representation of the Squeeze Theorem with g always below h and f in between.

Demonstration of how to use the Squeeze Theorem to find limits when direct substitution is not possible.

Example problem involving the limit of x^2 * cos(1/x^2) as x approaches 0.

Understanding the behavior of the cosine function to apply the Squeeze Theorem without needing the exact graph.

Multiplying the middle function by x^2 to create bounds for the Squeeze Theorem application.

Graphical illustration of the function being squeezed between negative x^2 and positive x^2.

Taking the limits of the bounds to deduce the limit of the middle function as x approaches 0.

Clarification that the Squeeze Theorem can be used when the limits of g and h are the same.

Practice problem involving the limit of a function f as x approaches 2 with given functions g and h.

Explanation that without the function f, the exact limit cannot be determined but must lie between the limits of g and h.

Note on the interval notation indicating when the inequality g < f < h holds true.

Guidance on attempting practice problems using the Squeeze Theorem with given functions.

Example of using the Squeeze Theorem to find the limit of a function as x approaches 0, where the limits of g and h are the same.

Clarification that the Squeeze Theorem cannot be used when the limits of the bounding functions are not equal.

Warning about the unbounded behavior of functions, which disqualifies the use of the Squeeze Theorem.

Final summary of the Squeeze Theorem and its application in finding limits of functions.

Transcripts

Browse More Related Video

AP Calculus AB - 1.8 Determining Limits Using the Squeeze Theorem

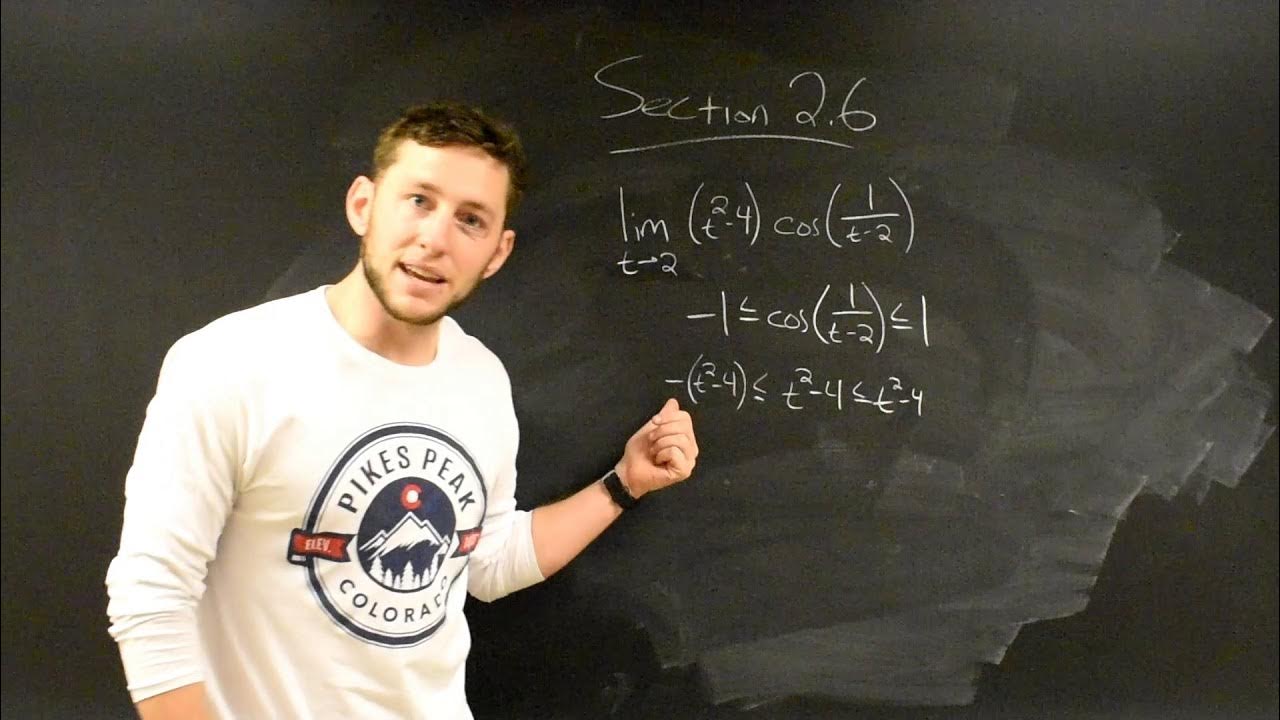
Limits Involving Sine and Cosine & The Squeeze Theorem!

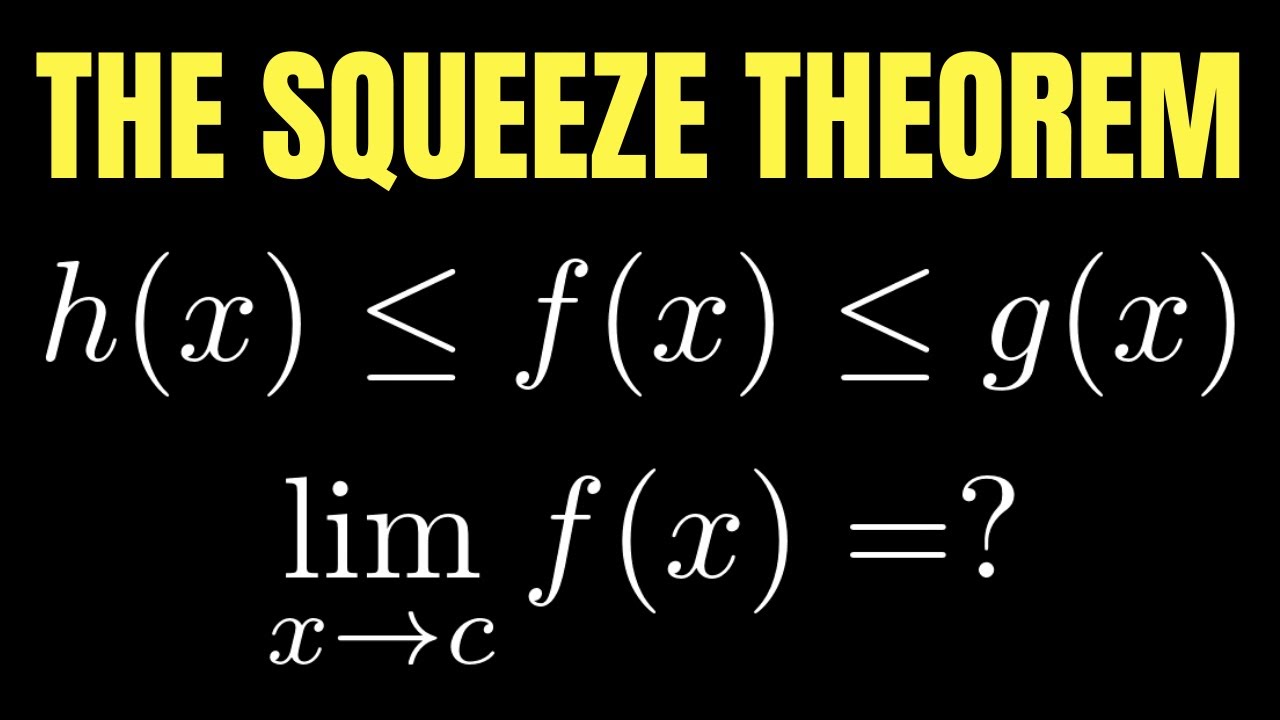
Calculus: The Squeeze Theorem Full Tutorial

The Squeeze Theorem for Limits, Example 1

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus

Zero-Bounded Limit Theorem (with example)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Squeeze TheoremCalculusLimitMathematicsEducationalTrigonometryGraphingMr. BeanTutorialAP Exam