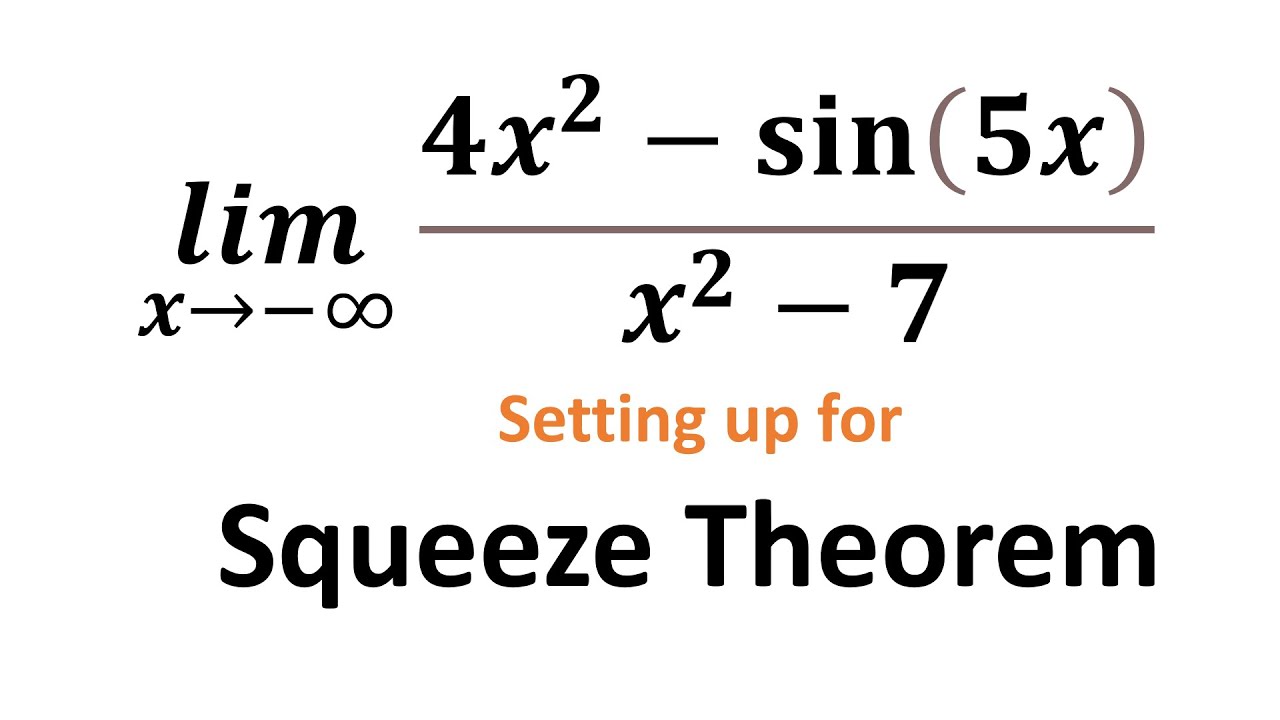Limits Involving Sine and Cosine & The Squeeze Theorem!

Ian Grigsby

4 Feb 202120:39

EducationalLearning

32 Likes 10 Comments

TLDRThis video provides an insightful summary of Section 2.6 from Rogowski's fourth edition calculus, focusing on the Squeeze Theorem and its application to trigonometric limits. The presenter begins with an example involving the limit of x^2 * sin(1/x) as x approaches 0, illustrating the theorem's utility when direct substitution fails. The Squeeze Theorem is effectively demonstrated through graphical analysis and algebraic bounding with x^2 and -x^2. The video also covers additional trigonometric limit rules derived from the Squeeze Theorem, emphasizing their importance in solving indeterminate forms. Examples are worked through to show how to manipulate expressions to fit these rules, including the use of trigonometric identities for double angles. The presenter concludes with a reminder of the theorem's power in finding limits that resist algebraic simplification, encouraging viewers to practice the techniques discussed for upcoming topics on infinite limits.

Takeaways

📚 The Squeeze Theorem is a method for finding limits when direct substitution or algebraic manipulation is not possible.
📈 To apply the Squeeze Theorem, you need to find an upper and a lower function that both approach the same limit as x approaches a certain value.
🔢 When the function in question is bounded between two other functions, and you know the limits of those bounding functions, you can determine the limit of the function in question.
🏗️ An example used in the video is the limit as x approaches 0 of x squared times sine(1/x), which is shown to be zero by bounding it with x squared and negative x squared.
📊 Graphing can provide intuition for the limit, but to prove it, you need to use mathematical bounds and the Squeeze Theorem.
🚫 Direct substitution is not always possible, especially when dealing with indeterminate forms like 0/0 or undefined expressions.
🧮 The properties of sine and cosine being bounded between -1 and 1 are used to create inequalities that help in applying the Squeeze Theorem.
🔄 The video demonstrates how to manipulate expressions to fit the form required by known limits, such as sine(kx)/kx as x approaches 0, which is known to be 1.
✅ The Squeeze Theorem confirms the limit found graphically by showing that the function is trapped between two functions that approach the same limit.
🔢 Two specific rules derived from the Squeeze Theorem are highlighted for their utility: sine(kx)/kx as x approaches 0 equals 1, and (1 - cosine(kx))/(kx) as x approaches 0 equals 0, given k is not zero.
⛓️ Trigonometric identities, such as the double angle formula, can be crucial in simplifying expressions before applying the Squeeze Theorem or other limit rules.

Q & A

What is the main topic of section 2.6 in Rogowski's fourth edition calculus?
-The main topic of section 2.6 is the Squeeze Theorem and its application to trigonometric limits.
Why is the Squeeze Theorem useful when finding limits?
-The Squeeze Theorem is useful when algebraic simplification is not possible, as it allows you to find the limit by bounding the function with an upper and a lower function that have the same limit.
What is the limit of x^2 * sin(1/x) as x approaches 0?
-The limit of x^2 * sin(1/x) as x approaches 0 is 0, which can be determined by using the Squeeze Theorem and observing the graph of the function.
How does the graph of y = x^2 * sin(1/x) behave as x approaches 0?
-As x approaches 0, the graph of y = x^2 * sin(1/x) appears to be approaching 0, even though direct substitution results in an undefined expression.
What are the two bounds proposed in the script for the function y = x^2 * sin(1/x)?
-The two bounds proposed are y = x^2 and y = -x^2, which both have the same limit of 0 as x approaches 0 and effectively 'squeeze' the function in question to the same limit.
What property of the sine function allows it to be bounded above by 1 and below by -1?
-The sine function takes an angle as input and returns a ratio of the lengths of the sides of a right triangle, which inherently limits its output to a range between -1 and 1.
What are the two trigonometric rules provided in the script that can be used for most of the homework problems?
-The two trigonometric rules are: (1) the limit as x approaches 0 of sin(kx)/kx is 1, and (2) the limit as x approaches 0 of (1 - cos(kx))/(kx) is 0, where k is any non-zero number.
How does the script use trigonometric identities to evaluate the limit of sin(3x)/sin(7x) as x approaches 0?
-The script uses the fact that sin(kx)/kx approaches 1 as x approaches 0 to transform the expression into a form that allows the application of this rule, resulting in a final answer of 3/7.
What is the issue with directly plugging in h=0 into the expression (1 - cos(2h))/sin^2(3h)?
-Directly plugging in h=0 results in an indeterminate form of 0/0 because the numerator and denominator both approach 0.
How does the double angle trigonometric identity help in evaluating the limit as h approaches 0 of (1 - cos(2h))/sin^2(3h)?
-The double angle identity allows the expression to be simplified to a form that can be evaluated using the Squeeze Theorem, ultimately leading to the limit being 2/9.
What is the next topic that will be discussed in the series after section 2.6?
-The next topic to be discussed is infinite limits.

Outlines

00:00

📚 Introduction to the Squeeze Theorem and Trig Limits

The video begins with an introduction to the Squeeze Theorem and its application in finding limits of trigonometric functions. The presenter uses the example of the limit as x approaches 0 of x squared times sine(1/x) to illustrate the theorem. After demonstrating that direct substitution is not applicable, the presenter turns to graphical analysis and upper and lower bounding functions to deduce the limit. The Squeeze Theorem is then proven by using these bounds, relying on the bounded nature of the sine function.

05:02

🔢 Applying the Squeeze Theorem to a Cosine Function

The second paragraph delves into applying the Squeeze Theorem to a more complex limit involving cosine. The presenter discusses the need to find upper and lower bounds for the function, which are carefully chosen to be functions that can be easily evaluated at the limit point. By using the bounds and the properties of absolute values, the presenter shows that the limit of the function as t approaches 2 is zero, reinforcing the concept of the Squeeze Theorem.

10:04

📉 Utilizing Trig Rules and Squeeze Theorem for Limits

The third paragraph focuses on using trigonometric rules derived from the Squeeze Theorem to find limits. Two specific rules are highlighted: the limit of sine(kx)/kx as x approaches 0, which equals 1, and the limit of (1 - cosine(kx))/kx as x approaches 0, which equals 0, assuming k is not zero. The presenter also addresses how to manipulate expressions to fit these rules and how to handle cases where the direct application of these rules might lead to indeterminate forms, thus necessitating the use of trigonometric identities.

15:07

🔁 Trig Identities and Squeeze Theorem in Limit Calculations

The fourth paragraph continues the discussion on trigonometric identities, particularly the double angle formula, and their role in resolving indeterminate forms that arise when applying the Squeeze Theorem. The presenter demonstrates this with an example involving the limit as h approaches 0 of (1 - cosine(2h))/(sine(3h))^2. By using the double angle identity and other trigonometric manipulations, the presenter simplifies the expression and successfully finds the limit to be 2/9, showcasing the utility of trigonometric identities in conjunction with the Squeeze Theorem.

20:07

🔄 Recap and Preview of Upcoming Topics

In the concluding paragraph, the presenter recaps the key points discussed in the video, emphasizing the utility of the Squeeze Theorem for finding limits that do not yield to algebraic simplification. The presenter also previews the next topic, which will be infinite limits, and encourages viewers to attempt their homework, wishing them good luck in their studies.

Mindmap

Keywords

💡Squeeze Theorem

The Squeeze Theorem is a fundamental theorem in calculus that allows the determination of a limit by bounding the function of interest between two other functions whose limits are known. In the video, it is used to find the limit of a function as x approaches 0, where direct substitution is not possible. The theorem is applied by identifying an upper bound and a lower bound that both converge to the same limit, thereby 'squeezing' the function in question to the same limit.

💡Trig Limits

Trig Limits refer to the limits of functions involving trigonometric functions as the variable approaches a certain value. In the context of the video, trig limits are discussed in relation to the Squeeze Theorem, where the limits of trigonometric functions are evaluated as they approach specific values, such as 0 or infinity. An example from the script involves finding the limit of sine of 1 over x as x approaches 0.

💡Graphing

Graphing is a visual method used to understand the behavior of functions, especially when dealing with limits. In the video, the presenter uses graphing to gain intuition about the limit of a function as x approaches 0. By observing the graph, one can see that the function appears to be approaching zero, which is later confirmed using the Squeeze Theorem.

💡Upper and Lower Bounds

Upper and lower bounds are values that constrain a function from above and below, respectively. In the video, the presenter creates bounds for the function x squared times sine of 1 over x using x squared as an upper bound and negative x squared as a lower bound. These bounds are crucial for applying the Squeeze Theorem to determine the limit of the function as x approaches 0.

💡Trigonometric Functions

Trigonometric functions, such as sine and cosine, are mathematical functions that describe the relationship between the angles and sides of a triangle. In the video, these functions are central to the limits being discussed. The presenter uses properties of these functions, such as their bounded nature, to apply the Squeeze Theorem and find limits of various expressions involving trigonometric functions.

💡Indeterminate Forms

Indeterminate forms arise in calculus when an expression cannot be simplified to a determinate value using basic algebraic operations. In the video, the script mentions an indeterminate form (0/0) when trying to find the limit of sine of 3x divided by sine of 7x as x approaches 0. The presenter then uses trigonometric identities and the Squeeze Theorem to resolve the indeterminate form and find the limit.

💡Trigonometric Identities

Trigonometric identities are equations that hold true for all values of the variables involved and are used to simplify trigonometric expressions. In the video, the presenter uses the double angle identity for cosine to simplify the expression 1 - cosine of 2h and apply the Squeeze Theorem. The identity states that cosine of 2 times an angle equals 1 - 2 times sine squared of the angle, which is crucial for finding the limit as h approaches 0.

💡Limit

In calculus, a limit is the value that a function approaches as the input (or argument) approaches a certain value. The concept of limits is central to the study of calculus and is used to define continuity, derivatives, and integrals. In the video, the presenter discusses various methods for finding limits, particularly when direct substitution results in an indeterminate form or when the function's behavior is not clear algebraically.

💡Algebraic Simplification

Algebraic simplification involves manipulating an algebraic expression to make it easier to solve or to express in a more straightforward form. In the video, the presenter mentions that when direct algebraic simplification is not possible, alternative methods like the Squeeze Theorem can be used to find limits. The script illustrates this when the presenter cannot simply substitute x with 0 in the expression x squared times sine of 1 over x.

💡Creative Multiplication

Creative multiplication is a technique used in calculus to manipulate expressions in a way that makes them easier to work with, often by introducing factors that can be canceled out. In the video, the presenter uses creative multiplication by introducing factors like 3x/3x and 7x/7x to transform the expression sine of 3x divided by sine of 7x into a form that can be analyzed using the Squeeze Theorem.

💡Substitution

Substitution is a method in calculus where one substitutes a complex expression with a simpler variable or a known pattern to simplify the problem. In the video, the presenter uses substitution to transform the expression involving sine and cosine functions into a form that can be evaluated using known limits and trigonometric identities. For instance, substituting h for 2h and 3h in the expression 1 - cosine of 2h allows the application of the Squeeze Theorem.

Highlights

Introduction to section 2.6 on the Squeeze Theorem and trigonometric limits.

Explaining the concept of trigonometric limits and how they differ from previous topics.

The demonstration of the limit of x^2 ⋅ sin(1/x) as x approaches 0 using a graphical approach.

Using the Squeeze Theorem to find limits when direct substitution is not possible.

The importance of creating bounds for a function to apply the Squeeze Theorem.

The property of the sine function being bounded between -1 and 1 as a key element in the Squeeze Theorem application.

The example of using the Squeeze Theorem to evaluate the limit of a function involving sine and x^2.

The explanation of how to manipulate the function to fit within the bounds required by the Squeeze Theorem.

The two additional rules derived from the Squeeze Theorem for common trigonometric limit scenarios.

The method of forcing a situation to match the derived rules by creative multiplication and rearrangement.

The application of trigonometric identities in evaluating limits, specifically the double angle identity.

The step-by-step process of using trigonometric identities and the Squeeze Theorem to evaluate complex limits.

The conclusion summarizing the key takeaways from the video, emphasizing the practical use of the Squeeze Theorem and trigonometric rules.

The anticipation of future topics, specifically infinite limits, to encourage viewers to engage with upcoming content.

Transcripts

Browse More Related Video

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus

SQUEEZE THEOREM - The Setup

Calculus AB/BC – 1.8 Determining Limits Using the Squeeze Theorem

Limits and Their Properties

Limits via Graphs!

Limit of x! over x^x as x goes to infinity

Related Tags

Squeeze Theorem Trig Limits Calculus Math Functions Graphing Inequalities Trigonometry Educational Content Theoretical Math Limit Evaluation