AP Calculus AB - 1.8 Determining Limits Using the Squeeze Theorem

Daniel Bortnick
4 Oct 202014:30
EducationalLearning
32 Likes 10 Comments

TLDRIn this calculus lesson, Mr. Bortnick introduces the Squeeze Theorem, also known as the Sandwich Theorem, which is a method for determining limits when direct substitution is not possible. He explains the theorem's conditions and demonstrates its application through several examples, including a limit involving cosine and x-squared. The lesson also covers scenarios where the theorem does not apply due to unequal limit values. Mr. Bortnick encourages students to practice with provided problems and seek clarification during class or office hours.

Takeaways
  • πŸ“š The topic of the day is the Squeeze Theorem, also known as the Sandwich Theorem, which is used to determine limits in calculus.
  • πŸ› οΈ The Squeeze Theorem states that if a function \( f(x) \) is squeezed between two other functions \( g(x) \) and \( h(x) \), and the limits of \( g(x) \) and \( h(x) \) as \( x \) approaches a certain value \( a \) are equal, then the limit of \( f(x) \) is also equal to that value.
  • ⚠️ The theorem can only be applied if the 'if' part of the statement is true, meaning \( g(x) \leq f(x) \leq h(x) \) and the limits of \( g(x) \) and \( h(x) \) are the same.
  • πŸ“‰ The first example demonstrates the theorem by showing that the limit of \( x^2 \cdot \cos(1/x^2) \) as \( x \) approaches 0 is 0, using the fact that the cosine function oscillates between -1 and 1.
  • 🚫 The second example shows a case where the Squeeze Theorem cannot be applied because the limits of \( g(x) \) and \( h(x) \) as \( x \) approaches 2 are not equal.
  • 🎯 The third example successfully applies the Squeeze Theorem to find that the limit of \( f(x) \) as \( x \) approaches 0 is 3, given that \( \cos(\pi/(2x+2)) \leq f(x) \leq x^2 + 3 \) and the limits of the outer functions are equal.
  • πŸ€” The final set of problems asks to determine whether the Squeeze Theorem can be applied to given inequalities to find limits as \( x \) approaches 0, with some being applicable and others not due to the limits of the outer functions not matching.
  • πŸ“‰ In the examples, the limits of functions are evaluated using direct substitution where possible, and the Squeeze Theorem is applied when the conditions are met.
  • πŸ“š The importance of understanding the behavior of functions, such as the range of the cosine function, is highlighted for effectively using the Squeeze Theorem.
  • πŸ“ The script encourages students to practice with the provided problems and to use class time and office hours for clarification of doubts.
Q & A

  • What is the Squeeze Theorem also known as?

    -The Squeeze Theorem is sometimes referred to as the Sandwich Theorem or the Pinching Theorem.

  • What is the basic premise of the Squeeze Theorem?

    -The Squeeze Theorem states that if a function f(x) is surrounded by two other functions g(x) and h(x), such that g(x) ≀ f(x) ≀ h(x), and the limits of g(x) and h(x) as x approaches a certain value are equal, then the limit of f(x) as x approaches that value is also equal to that limit.

  • What is an example of a trigonometric function that cannot be solved using direct substitution?

    -An example given in the script is the limit as x approaches 0 of x squared times cosine of 1 over x squared, which cannot be solved using direct substitution due to division by zero.

  • What is the range of the cosine function?

    -The range of the cosine function is between -1 and 1, inclusive.

  • How does the Squeeze Theorem help in finding the limit of the function x squared times cosine of 1 over x squared as x approaches 0?

    -The Squeeze Theorem helps by establishing that the function is bounded between -x squared and x squared, both of which have a limit of 0 as x approaches 0, thus the limit of the original function must also be 0.

  • What is the significance of the limits of g(x) and h(x) in the Squeeze Theorem?

    -The limits of g(x) and h(x) must be equal and approach the same value as x approaches the point in question for the Squeeze Theorem to be applicable and conclude the limit of f(x).

  • Why can't the Squeeze Theorem be used to find the limit as x approaches 2 of a function f(x) when g(x) = -x squared + 2x - 3 and h(x) = 2x + 1?

    -The Squeeze Theorem cannot be used in this case because the limits of g(x) and h(x) as x approaches 2 are not equal, which violates the condition that the limits must be the same for the theorem to apply.

  • What is the limit as x approaches 0 of the function f(x) given g(x) = cosine of pi over 2x + 2 and h(x) = x squared + 3?

    -The limit as x approaches 0 of f(x) is 3, as both g(x) and h(x) evaluate to 3 at x = 0, satisfying the conditions of the Squeeze Theorem.

  • What conditions must be met for the Squeeze Theorem to be applicable for a function f(x) as x approaches zero?

    -For the Squeeze Theorem to be applicable, there must be functions g(x) and h(x) such that g(x) ≀ f(x) ≀ h(x) for all x in a neighborhood of zero, and the limits of g(x) and h(x) as x approaches zero must be equal.

  • Why does the Squeeze Theorem apply to the limit as x approaches 0 of g(x) = -x cubed + 1 and h(x) = x cubed + 1?

    -The Squeeze Theorem applies because both g(x) and h(x) evaluate to 1 as x approaches 0, indicating that the limit of f(x), if it exists and is squeezed between g(x) and h(x), must also be 1.

Outlines
00:00
πŸ“š Introduction to the Squeeze Theorem

This paragraph introduces the concept of the Squeeze Theorem, also known as the Sandwich Theorem, in the context of calculus. The theorem is explained as a method to determine limits when direct substitution is not possible due to division by zero or other undefined expressions. The basic premise is that if a function 'f(x)' is 'squeezed' between two other functions 'g(x)' and 'h(x)', and both 'g(x)' and 'h(x)' have the same limit 'l' as 'x' approaches a certain value 'a', then 'f(x)' must also have the limit 'l'. The explanation includes a step-by-step breakdown of the conditions required to apply the theorem and an example involving the limit of 'x^2 * cos(1/x^2)' as 'x' approaches 0, which cannot be solved through direct substitution but can be determined using the Squeeze Theorem.

05:02
πŸ” Applying the Squeeze Theorem to Example Problems

The second paragraph delves into applying the Squeeze Theorem to solve specific calculus problems. It starts with an example of finding the limit of 'x^2 * cos(1/x^2)' as 'x' approaches 0, using the known range of the cosine function to establish the bounds for the squeeze. The paragraph then discusses two additional problems involving functions 'g(x)' and 'h(x)', and a function 'f(x)' that is bounded by them. The first example demonstrates the successful application of the theorem, concluding that the limit of 'f(x)' as 'x' approaches 2 is 0. The second example shows a case where the theorem cannot be applied because the limits of 'g(x)' and 'h(x)' as 'x' approaches 2 are not equal, thus the limit of 'f(x)' cannot be determined using the Squeeze Theorem.

10:03
πŸ“˜ Further Exploration of the Squeeze Theorem

The third paragraph continues the exploration of the Squeeze Theorem with additional examples. It discusses the limit of 'f(x)' as 'x' approaches 0, where 'f(x)' is bounded by 'cos(pi/(2x) + 2)' and 'x^2 + 3'. The limits of the bounding functions are evaluated, and it is shown that they are equal, allowing the application of the Squeeze Theorem to conclude that the limit of 'f(x)' is 3. The paragraph also addresses a set of problems where the theorem's applicability is questioned for different inequalities. It explains which inequalities can be used with the theorem based on whether the limits of the bounding functions are the same, and which cannot, providing clear criteria for the theorem's use.

Mindmap
Keywords
πŸ’‘Squeeze Theorem
The Squeeze Theorem, also known as the Sandwich Theorem, is a fundamental concept in calculus that allows for the determination of a limit by 'squeezing' a function between two others. It is central to the video's theme of limit determination. The theorem states that if two functions, g(x) and h(x), bracket another function f(x), and the limits of g(x) and h(x) as x approaches a certain value are equal, then the limit of f(x) as x approaches that value must also be equal to this common limit. The script uses the theorem to solve examples where direct substitution is not feasible.
πŸ’‘Limit
A limit in calculus is the value that a function or sequence 'approaches' as the input or index approaches some value. It is a foundational concept for understanding continuity and differentiability. The script discusses determining limits using the Squeeze Theorem, emphasizing the process of finding what value a function approaches as its input gets arbitrarily close to a specific point, such as when x approaches 0.
πŸ’‘Continuity
Continuity refers to the property of a function where it is defined at every point in its domain and its graph does not have any 'gaps' or 'jumps.' While not explicitly defined in the script, continuity is an underlying theme as limits are a prerequisite for discussing continuity. The script's focus on limits indirectly touches upon the concept of continuity since a function is continuous at a point if the limit exists and is equal to the function's value at that point.
πŸ’‘Cosine Function
The cosine function is a trigonometric function that describes a wave with a period of 2Ο€. It is mentioned in the script in the context of using the Squeeze Theorem to find the limit of a function involving cosine. The range of the cosine function, which oscillates between -1 and 1, is used to establish an inequality that helps in applying the theorem.
πŸ’‘Periodic Function
A periodic function is one that repeats its values at regular intervals or periods. The cosine function, mentioned in the script, is an example of a periodic function with a period of 2Ο€. This property is leveraged in the script to understand the behavior of the function within the context of the Squeeze Theorem.
πŸ’‘Direct Substitution
Direct substitution is a method in calculus where you substitute the value of x that the limit is approaching directly into the function to find the limit. The script mentions that direct substitution is not always possible, as in the case of the function x^2 times cosine(1/x^2), where substitution leads to an undefined expression due to division by zero.
πŸ’‘Inequality
Inequalities are mathematical statements that compare expressions, indicating that one is less than, greater than, or equal to another. In the context of the Squeeze Theorem, inequalities are used to establish the relationship between the functions f(x), g(x), and h(x). The script provides examples of inequalities that must hold true for the theorem to be applied.
πŸ’‘Conditional Statement
A conditional statement in mathematics, often structured as 'if...then...', is used to express a logical relationship where one statement is true if and only if another is true. The script describes the Squeeze Theorem as a conditional statement, where the conditions are the inequalities between the functions and the conclusion is the determination of the limit of f(x).
πŸ’‘Graphing Calculator
A graphing calculator is a device used to graph functions and equations, which can be helpful in visualizing mathematical concepts. The script suggests using a graphing calculator to investigate the range of the cosine function, illustrating how technology can assist in understanding the behavior of functions.
πŸ’‘Trigonometric Rules
Trigonometric rules are mathematical relationships involving trigonometric functions like sine and cosine. The script refers to 'special trig rules' that students may have memorized, which are not applicable in the case of the given function involving cosine. This highlights the limitations of certain mathematical techniques and the need for alternative methods like the Squeeze Theorem.
Highlights

Introduction to the Squeeze Theorem, also known as the Sandwich Theorem or Pinching Theorem, and its formal definition.

Explanation of how the Squeeze Theorem works with three functions, where the middle function is 'squeezed' between the other two.

Conditional statement aspect of the Squeeze Theorem, requiring all conditions to be true before reaching a conclusion.

Practical example of using the Squeeze Theorem to find the limit of a function involving cosine, where direct substitution fails.

Utilization of the range of the cosine function (-1 to 1) to set up the inequality for the Squeeze Theorem.

Multiplication of the inequality by x squared to fit the form required for the Squeeze Theorem application.

Evaluation of limits for the outer functions in the inequality to determine the limit of the middle function.

Conclusion that the limit of x squared times cosine of 1 over x squared as x approaches 0 is 0, using the Squeeze Theorem.

Second example with functions g(x) and h(x), where the Squeeze Theorem is applied to find the limit as x approaches 2 of an unknown function f(x).

Demonstration that the Squeeze Theorem cannot be applied if the limits of the outer functions are not equal.

Third example with functions g(x) and h(x) defined differently, and the successful application of the Squeeze Theorem to find the limit as x approaches 0 of f(x).

Final conclusion that the limit as x approaches 0 of f(x) equals 3, based on the equality of the limits of the outer functions.

Discussion of a set of problems where the applicability of the Squeeze Theorem is to be determined, not the limit itself.

Analysis of inequalities to determine if the Squeeze Theorem can be used, based on whether the limits of the outer functions are the same.

Examples where the Squeeze Theorem does not apply due to the limits of the outer functions not being equal.

Examples where the Squeeze Theorem does apply, leading to the determination of the limit of the function as x approaches 0.

Final note on the importance of checking the equality of the limits for the Squeeze Theorem to be applicable.

Encouragement for students to practice problems, check answers, and bring questions to class for further discussion.

Transcripts

Browse More Related Video

Calculus AB/BC – 1.8 Determining Limits Using the Squeeze Theorem

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus

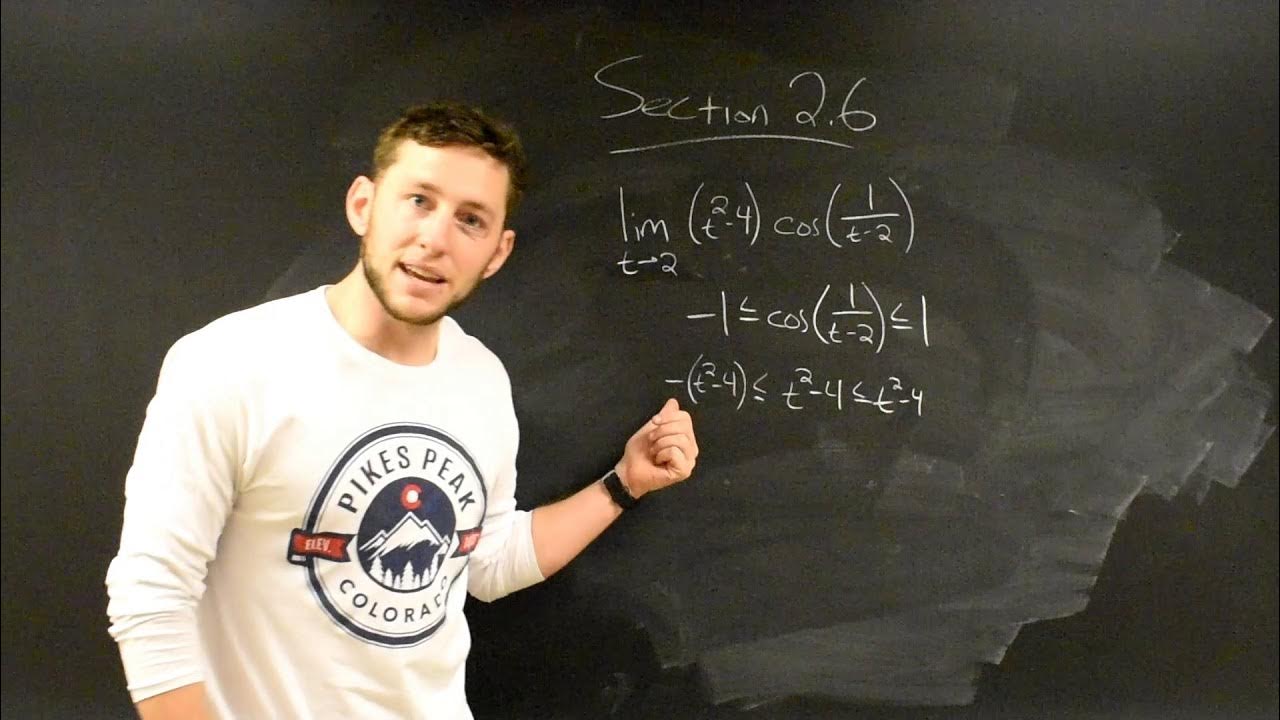
Limits Involving Sine and Cosine & The Squeeze Theorem!

AP Calculus AB - 1.6b Determining Limits Using Algebraic Manipulation

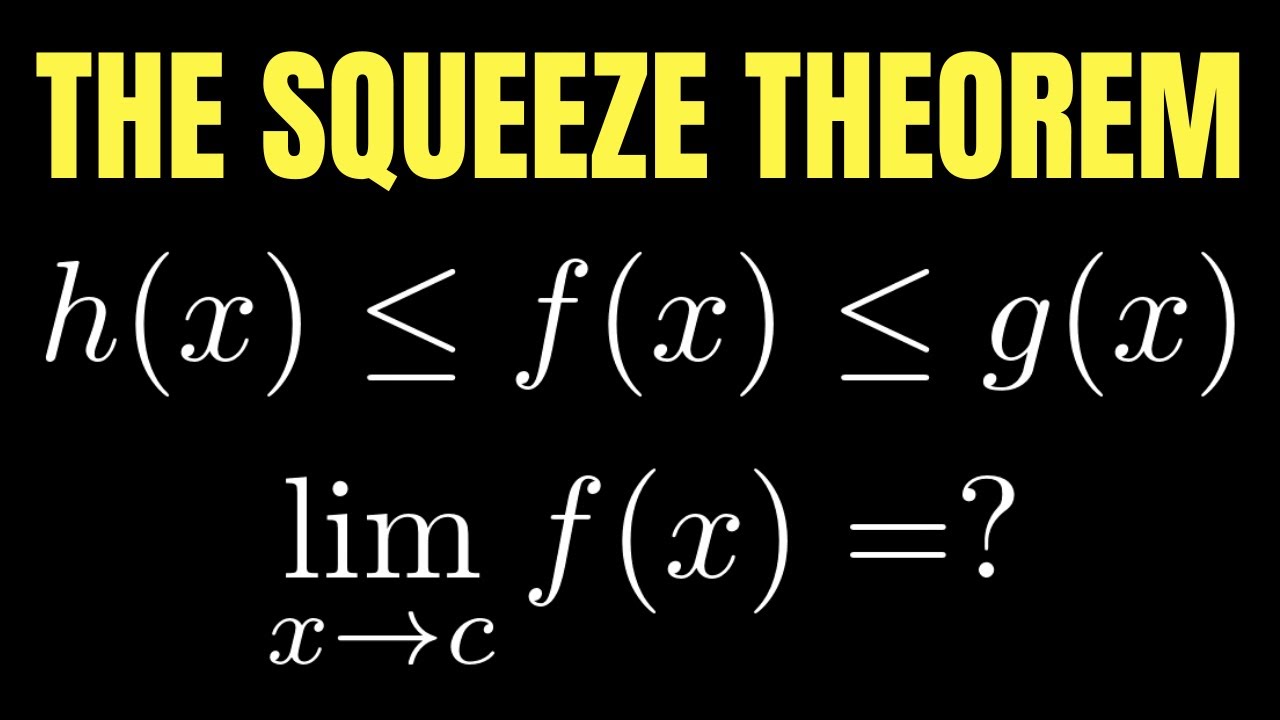
Calculus: The Squeeze Theorem Full Tutorial

AP Calculus AB - 1.9 Connecting Multiple Representations of Limits

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusLimitsContinuitySqueeze TheoremTrigonometryAlgebraLecture NotesEducational ContentMathematicsAP Calculus