How To Find The Unit Vector

The Organic Chemistry Tutor
24 Feb 201905:08
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script focuses on finding the unit vector of a given vector. It first explains the concept of a unit vector, which has the same direction as the original vector but a magnitude of one. The script then provides a step-by-step solution for finding the unit vector of vector v, demonstrating the calculation of the vector's magnitude and dividing each component by this magnitude to normalize it. It also offers an additional example with vector w, showing how to simplify the square root of the sum of squares when the magnitude is not a perfect square, and how to rationalize the denominator for a more simplified expression. The lesson concludes with a reminder to subscribe and engage with the content.

Takeaways
  • 📚 The lesson focuses on finding the unit vector of a given vector.
  • 🔍 The formula for the unit vector \( \mathbf{u} \) is \( \mathbf{v} \) divided by the magnitude of \( \mathbf{v} \).
  • 🧭 The unit vector has the same direction as the original vector but a magnitude of one.
  • 📐 For vector \( \mathbf{v} = 4, -3 \), the magnitude is calculated as \( \sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \).
  • 🔢 The unit vector for \( \mathbf{v} \) is \( \frac{4}{5}, \frac{-3}{5} \).
  • 📈 The magnitude of a vector \( \mathbf{w} \) is calculated by taking the square root of the sum of the squares of its components.
  • 🔄 For vector \( \mathbf{w} = -8, 4 \), the magnitude is \( \sqrt{(-8)^2 + 4^2} = \sqrt{64 + 16} = \sqrt{80} \).
  • ✂️ The square root of 80 is simplified to \( 4\sqrt{5} \) by factoring out the highest perfect square, which is 16.
  • 📝 The unit vector for \( \mathbf{w} \) is \( \frac{-8}{4\sqrt{5}}, \frac{4}{4\sqrt{5}} \) which simplifies to \( -\frac{2}{\sqrt{5}}, \frac{1}{\sqrt{5}} \).
  • 📚 Further simplification can be achieved by rationalizing the denominator, resulting in \( -2\sqrt{5}/5, \sqrt{5}/5 \).
  • 📘 The final unit vector can be presented in either simplified form or with a rationalized denominator, depending on preference or teacher's instructions.
Q & A

  • What is the main focus of the lesson in the provided transcript?

    -The main focus of the lesson is finding the unit vector of a given vector.

  • What is a unit vector?

    -A unit vector is a vector that has the same direction as the original vector but a magnitude of one.

  • How is the unit vector denoted in the script?

    -The unit vector is denoted as 'u' in the script.

  • What is the formula used to find the unit vector of vector 'v'?

    -The formula used to find the unit vector 'u' of vector 'v' is u = v / (magnitude of v).

  • What are the components of vector 'v' given in the script?

    -The components of vector 'v' are 4 and -3.

  • How is the magnitude of vector 'v' calculated in the script?

    -The magnitude of vector 'v' is calculated as the square root of (4^2 + (-3)^2), which simplifies to the square root of 25, and equals 5.

  • What is the resulting unit vector for vector 'v'?

    -The resulting unit vector for vector 'v' is 4/5, -3/5.

  • What is the process to simplify the radical when the magnitude of a vector is not a perfect square?

    -The process involves breaking down the number under the radical into a product of a perfect square and another number, then simplifying the expression accordingly.

  • What is the magnitude of vector 'w' calculated in the script?

    -The magnitude of vector 'w' is calculated as the square root of (-8^2 + 4^2), which simplifies to 4 times the square root of 5.

  • How is the unit vector for vector 'w' simplified in the script?

    -The unit vector for vector 'w' is simplified by dividing each component by the magnitude (4√5), resulting in -2/√5 times the unit vector i and 1/√5 times the unit vector j.

  • What is the final simplified form of the unit vector for vector 'w' after rationalizing the denominator?

    -The final simplified form of the unit vector for vector 'w' is -2√5/5 and √5/5.

  • How does the script suggest rationalizing the denominator of the unit vector?

    -The script suggests multiplying the numerator and denominator by √5 to rationalize the denominator.

  • What is the significance of rationalizing the denominator in the context of the script?

    -Rationalizing the denominator simplifies the expression and makes it easier to work with in further calculations, although it is optional based on the preference of the teacher or the individual.

Outlines
00:00
📚 Finding the Unit Vector of a Given Vector

This paragraph explains the concept of finding the unit vector of a given vector. It begins by introducing the formula for the unit vector 'u', which is the original vector 'v' divided by its magnitude. The magnitude of vector 'v' is calculated by taking the square root of the sum of the squares of its components. The example provided uses vector 'v' with components (4, -3), and the magnitude is found to be 5. The unit vector is then calculated by dividing each component by the magnitude, resulting in (4/5, -3/5). The paragraph also includes a second example with vector 'w' having components (-8, 4), where the magnitude is simplified to 4√5. The unit vector for 'w' is obtained by dividing each component by this magnitude, resulting in (-2/√5, 1/√5), which can be further rationalized for simplicity.

05:02
👍 Closing Remarks and Viewer Engagement

The final paragraph serves as a conclusion to the video, encouraging viewers to engage with the content. It reminds viewers to subscribe to the channel, activate notifications, and like the video. This call to action is a common practice to increase viewer interaction and build a community around the content.

Mindmap
Keywords
💡Unit Vector
A unit vector is a vector that has a magnitude of one and points in the same direction as the original vector. It is a fundamental concept in vector mathematics, used to normalize vectors to a standard length for comparison or further calculations. In the video, the unit vector 'u' is calculated by dividing vector 'v' by its magnitude, resulting in a vector that maintains the direction of 'v' but has a length of one.
💡Vector
A vector is a mathematical object that has both magnitude and direction. In physics and engineering, vectors are used to represent quantities such as force or velocity, which have both size and direction. In the script, vectors 'v' and 'w' are given in component form, and the process of finding their unit vectors is demonstrated.
💡Component Form
Component form is a way to represent a vector by its individual components along the coordinate axes, typically x and y in two dimensions. It is a standard method for expressing vectors in terms of their directional parts. In the script, vector 'v' is given as '4, -3', indicating its components along the x and y axes.
💡Magnitude
The magnitude of a vector is its length or size, which is a scalar quantity. It is calculated using the Pythagorean theorem for two-dimensional vectors. In the video, the magnitude of vector 'v' is found by taking the square root of the sum of the squares of its components, which is 5 in this case.
💡Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a mathematical operation used to find the magnitude of a vector, as seen in the script where the square root of the sum of the squares of the components is taken to find the magnitude of vectors 'v' and 'w'.
💡Simplifying Radicals
Simplifying radicals involves expressing the radical in its simplest form, often by factoring out perfect squares. In the script, the square root of 80 is simplified by recognizing that 16 is a perfect square within 80, resulting in the simplified form of 4√5.
💡Rationalizing the Denominator
Rationalizing the denominator is a process used to eliminate radicals from the denominator of a fraction, which is often done to simplify expressions or to prepare for further calculations. In the video, the denominator is rationalized by multiplying the numerator and denominator by √5, resulting in a simplified unit vector with rational numbers.
💡Direction
The direction of a vector is the direction in which it points. It is one of the two main attributes of a vector, along with magnitude. The unit vector derived from any vector 'v' will have the same direction as 'v', which is important for maintaining the orientation in vector operations.
💡Example Problem
An example problem is a specific instance of a mathematical problem that is used to illustrate a concept or method. In the script, two example problems are provided to demonstrate the process of finding the unit vector of a given vector.
💡Subscription and Notification Bell
These terms refer to features on video platforms like YouTube, where viewers can subscribe to a channel and enable notifications to be alerted when new content is posted. The script encourages viewers to subscribe and click the notification bell, which is a common practice to grow a channel's audience.
Highlights

Lesson focuses on finding the unit vector of a given vector.

Unit vector u is defined as vector v divided by the magnitude of v.

Unit vector has the same direction as vector v but a magnitude of one.

Vector v is given in component form as (4, -3).

Magnitude of vector v is calculated as the square root of 4^2 + (-3)^2.

Magnitude calculation results in √(16 + 9) = √25 = 5.

Unit vector for vector v is (4/5, -3/5).

Introduction of a second example with vector w.

Vector w is given as (-8, 4).

Magnitude of vector w is calculated as √((-8)^2 + 4^2).

Magnitude calculation results in √(64 + 16) = √80.

80 is simplified to √(16 * 5) = 4√5.

Unit vector for vector w is (-8/(4√5), 4/(4√5)).

Further simplification leads to unit vector components (-2/√5, 1/√5).

Option to rationalize the denominator for a more simplified form.

Rationalization results in unit vector components (-2√5/5, √5/5).

Preference for the simplified form due to less writing and clarity.

End of the video with a call to action for likes and subscriptions.

Transcripts

Browse More Related Video

Unit Vectors & Scalar Multiplication (in 3 dimensions)

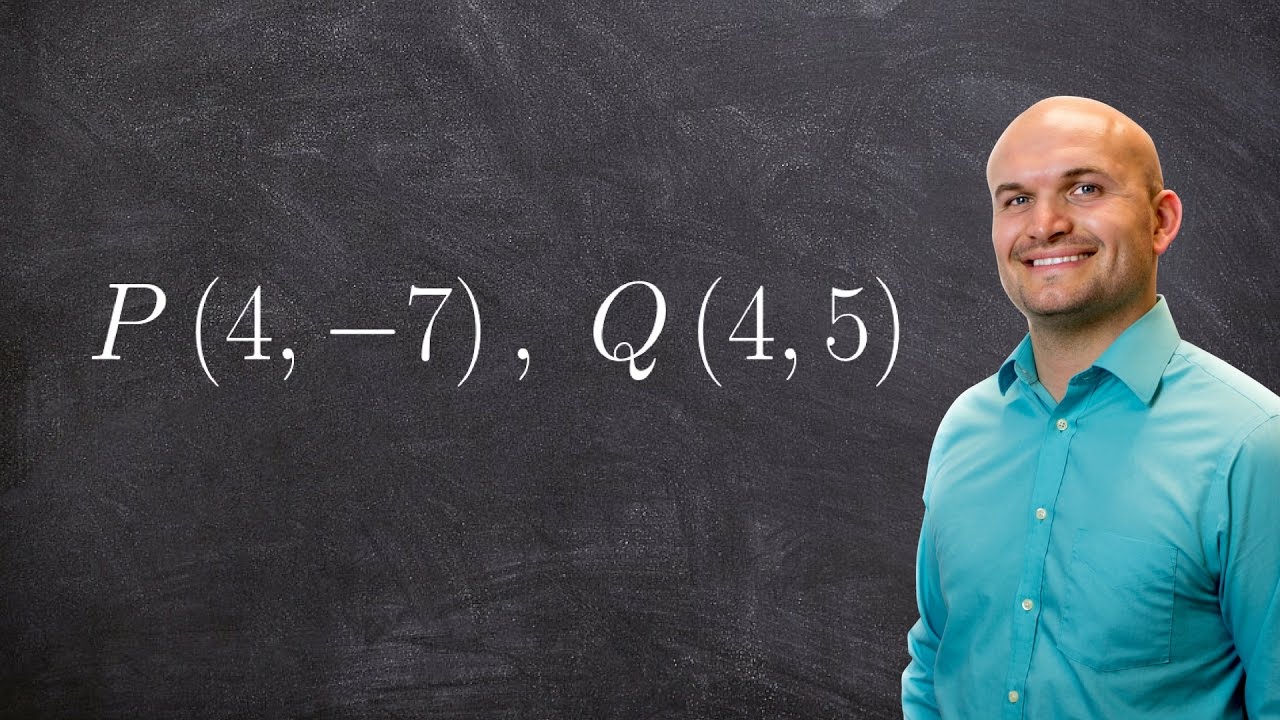
How to find the component form and magnitude of a vector

Unit Tangent Vector & Principal Unit Normal Vector (Calculus 3)

Vector components from magnitude and direction

How to Find Magnitude & Direction of Vectors

AP Physics B Kinematics Presentation #50

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Unit VectorVector MagnitudeMathematicsCalculusTutorialEducationVector DivisionSimplificationVector AnalysisRationalization