Mode, Median, Mean, Range, and Standard Deviation (1.3)

Simple Learning Pro
16 Oct 201507:10
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into key statistical concepts, including mode, median, mean, range, and standard deviation, which are pivotal for understanding data distribution. It explains how mode is the most frequently occurring value, median as the middle value in an ordered set, and mean as the average. The script also covers how to calculate these measures, emphasizing the median's position for odd and even datasets. Furthermore, it distinguishes between measures of central tendency and spread, illustrating the calculation of range and standard deviation with a step-by-step approach. Variance is also briefly mentioned, highlighting its relationship with standard deviation. The script serves as an informative guide for anyone looking to grasp the fundamentals of statistical analysis.

Takeaways
  • 📊 The video discusses five key statistical measures: mode, median, mean, range, and standard deviation.
  • 🔢 Mode is the value that appears most frequently in a dataset, and in the example, the mode is 154.
  • 🎯 Median is the middle value in an ordered dataset, and it is 154 in the provided example with an odd number of data points.
  • 📈 To find the median in a large dataset, the formula (n + 1) / 2 can be used to determine its position.
  • 📚 If the dataset has an even number of values, the median is the average of the two middle numbers, as shown with the calculation of 154.5.
  • 🧮 Mean, or arithmetic average, is calculated by summing all data values and dividing by the total number of values, resulting in 165.6 for the example.
  • ⚖️ Median and mean are both measures of central tendency but represent the center of the dataset in different ways.
  • 📏 Range is a measure of spread, calculated by subtracting the smallest value from the largest, which is 57 in the example.
  • 🔍 Standard deviation is a measure of how spread out the values are around the mean, calculated using a specific formula and resulting in 4.336 for the example.
  • 📉 A small standard deviation indicates less variability and values closer to the mean, whereas a large standard deviation indicates more spread.
  • 📊 Variance is closely related to standard deviation but does not involve taking the square root of the calculations, denoted as s² for sample variance.
Q & A

  • What are the five numerical measures discussed in the video?

    -The five numerical measures discussed in the video are mode, median, mean, range, and standard deviation.

  • What is the mode of a dataset?

    -The mode of a dataset is the data value that appears most frequently. In the example given, the mode is 154 since it appears three times.

  • How is the median of a dataset determined?

    -The median is the middle value of an ordered dataset. If the dataset has an odd number of values, the median is the value in the exact middle. For an even number of values, the median is the average of the two middle values.

  • What formula is used to find the position of the median in a dataset?

    -The formula used to find the position of the median is n + 1/2, where n is the total number of data values in the sample.

  • What is the mean of a dataset?

    -The mean, also known as the arithmetic average, is calculated by summing all data values and dividing by the total number of data values.

  • How does the median differ from the mean as a measure of central tendency?

    -The median represents the physical middle point of a dataset, while the mean represents the balance point or average value. The median is less affected by outliers, whereas the mean can be skewed by extreme values.

  • What is the range of a dataset?

    -The range is the difference between the maximum and minimum values in a dataset, indicating the spread or dispersion of the data.

  • How is the standard deviation calculated?

    -The standard deviation is calculated by taking the square root of the variance, which is the average of the squared differences from the mean.

  • What does a small standard deviation indicate about a dataset?

    -A small standard deviation indicates that the data points are closely clustered around the mean, suggesting less variability and a more concentrated distribution.

  • What is variance and how does it relate to standard deviation?

    -Variance is a measure of the spread of a dataset and is closely related to standard deviation. The only difference is that variance does not involve taking the square root of the calculations, unlike standard deviation.

  • How can you determine if a dataset is more spread out based on its standard deviation?

    -If the standard deviation is high, it indicates a high amount of variability, meaning that there are more values that are farther from the mean, which makes the distribution more spread out.

Outlines
00:00
📊 Understanding Measures of Central Tendency and Spread

This paragraph introduces the statistical concepts of mode, median, mean, range, and standard deviation as numerical ways to describe the distribution of a dataset. The mode is the most frequently occurring value, illustrated with an example where the mode is 154 cm in a dataset of nine people's heights. The median is the middle value when data is ordered, which in this case is also 154 cm. The mean, or arithmetic average, is calculated by summing all values and dividing by the total count, resulting in a mean height of 165.6 cm for the sample. The paragraph also explains how to calculate the median for both odd and even numbers of data points and compares the median to the mean as measures of central tendency. Additionally, it introduces measures of spread, such as range and standard deviation, with the range being the difference between the maximum and minimum values.

05:02
📈 Calculating and Interpreting Standard Deviation and Variance

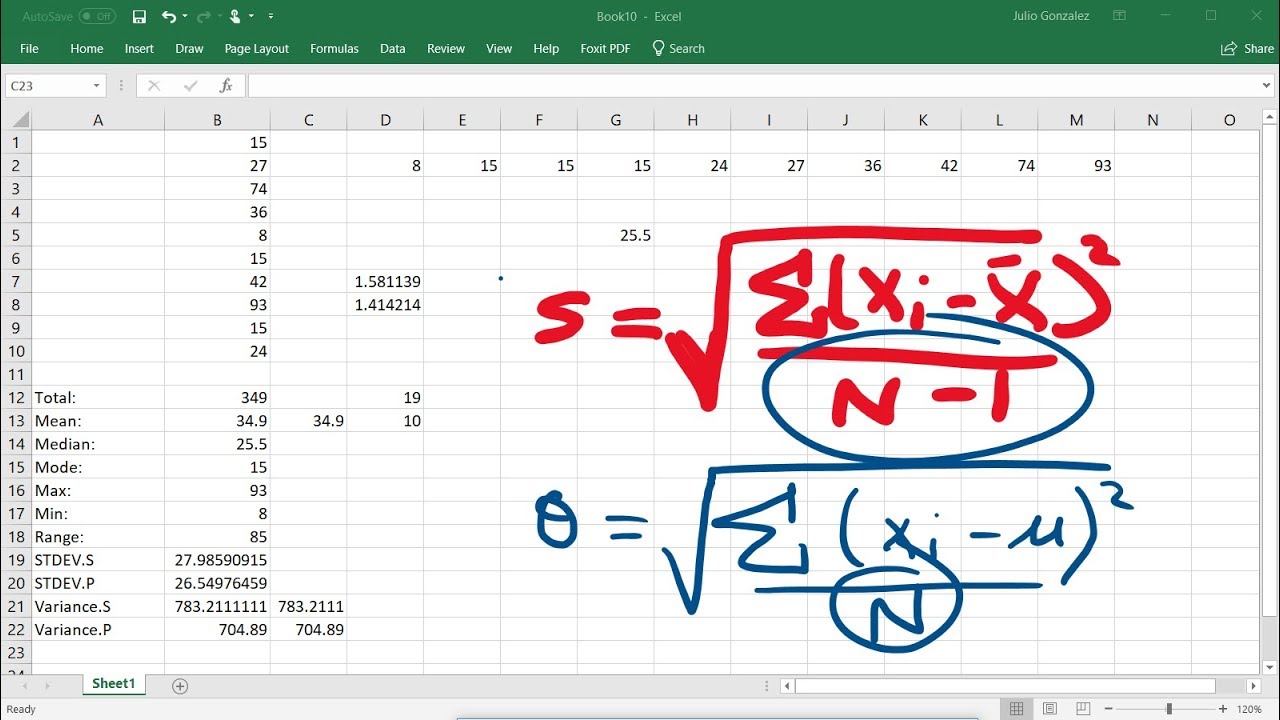
The second paragraph delves into calculating the standard deviation, which measures the amount of variation or dispersion in a dataset. It uses a step-by-step process to demonstrate the calculation, starting with finding the mean, then subtracting each data point from the mean, squaring the results, summing them up, and finally dividing by the total number of data points to find the variance. The standard deviation is the square root of the variance. The example provided calculates a standard deviation of 4.336 for a dataset with a mean of 15.4. The paragraph explains that a small standard deviation indicates less variability and a more concentrated distribution around the mean, while a large standard deviation suggests greater variability and a more spread-out distribution. It also touches on variance, which is closely related to standard deviation but does not involve taking the square root, and both can be referred to as sample variance and sample standard deviation.

Mindmap
Keywords
💡Mode
The mode in statistics refers to the value that appears most frequently in a data set. It is a measure of central tendency, which means it indicates the 'middle' value of the data. In the video script, the mode is exemplified by the number 154, which appears three times in the given data set of nine people's heights, making it the most frequently observed value.
💡Median
The median is another measure of central tendency, representing the middle value of a data set when it is ordered from smallest to largest. If there is an odd number of data points, the median is the exact middle value. In the script, the median is found to be 154, as it is the middle value with four data points on either side. For an even number of data points, the median is calculated as the average of the two middle numbers, which is demonstrated in the script with the calculation of 154.5.
💡Mean
The mean, also known as the arithmetic average, is a measure of central tendency calculated by summing all the values in a data set and then dividing by the number of values. It represents the 'average' value of the data set. In the video, the mean is calculated by adding all the heights and dividing by the total number of people, resulting in a mean (x-bar) of 165.6.
💡Range
The range is a measure of spread or dispersion in a data set, indicating the difference between the maximum and minimum values. It provides a simple way to understand the overall spread of the data. In the script, the range is calculated by subtracting the smallest height (139) from the largest height (196), resulting in a range of 57.
💡Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. It indicates how spread out the numbers are from the mean. A low standard deviation means that the data points are close to the mean, while a high standard deviation indicates that the data points are spread out over a wider range. In the video, the standard deviation is calculated using a formula that involves squaring the differences between each data point and the mean, summing these squares, and then taking the square root of the result, which is found to be 4.336.
💡Histograms
Histograms are a graphical representation of data, where data is grouped into ranges or 'bins' and the frequency of data points within each bin is represented by the height of the bars. They help visualize the distribution of a data set. Although not the main focus of the video, histograms are mentioned as a way to display a dataset, which complements the numerical measures discussed.
💡Stem Plots
Stem plots are a method of displaying data graphically, where the stem represents the higher order digits and the leaves represent the lower order digits. They are useful for spotting patterns or outliers in the data. The script briefly mentions stem plots as another way to visually display a data set, alongside histograms and pie charts.
💡Pie Charts
Pie charts are circular statistical graphics that are used to display data in a way that the size of each 'slice' of the pie is proportional to the quantity it represents. They are mentioned in the script as a visual tool for displaying a dataset, although they are not directly related to the numerical measures of central tendency or spread discussed in the video.
💡Central Tendency
Central tendency refers to the concept of finding a central or typical value in a data set. The mode, median, and mean are all measures of central tendency that provide different perspectives on the 'middle' of the data. The video script focuses on these three measures to explain how they can numerically describe the distribution of a data set.
💡Spread
In statistics, spread refers to the dispersion or variability of data points in a set. The range and standard deviation are measures of spread that help to understand how data points are distributed relative to each other. The script discusses these measures to explain how they can numerically describe the variability within a data set.
💡Variance
Variance is a measure of dispersion that is closely related to standard deviation. It represents the average of the squared differences from the mean. The only difference between variance and standard deviation is that variance does not involve taking the square root of the sum of squared differences. In the script, variance is mentioned as a concept that complements the understanding of standard deviation, with the formula for variance being the square of the standard deviation.
Highlights

The video discusses mode, median, mean, range, and standard deviation as numerical ways to describe a data distribution.

Mode is the most frequently observed data value in a dataset.

Median is the middle data value in an ordered dataset.

To find the median, data must be ordered from smallest to largest.

For an ordered dataset with an odd number of values, the median is the middle value.

For a large dataset, the median's position can be found using the formula n + 1/2.

If the dataset has an even number of values, the median is the average of the two middle values.

Mean, or arithmetic average, is calculated by summing all data values and dividing by the total number.

Mean represents the balance point of a dataset, like a seesaw.

Range is the difference between the maximum and minimum values in a dataset.

Standard deviation measures the amount of variation or dispersion in a dataset.

A small standard deviation indicates values are close to the mean, while a large one indicates greater variability.

Variance is closely related to standard deviation, differing only in the absence of the square root in its calculation.

Variance and standard deviation can both be referred to as sample variance and sample standard deviation.

The video provides a step-by-step guide on calculating the standard deviation using a formula.

The standard deviation is computed by finding the average of the squared differences from the mean.

The video uses a table to demonstrate the calculation process for standard deviation.

Transcripts

Browse More Related Video

Calculating The Standard Deviation, Mean, Median, Mode, Range, & Variance Using Excel

Mean, Median and Mode - Measures of Central Tendency

Math 119 Chapter 3 part 2

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

Elementary Statistics - Chapter 3 Describing Exploring Comparing Data Measure of Central Tendency

Range, variance and standard deviation as measures of dispersion | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsData AnalysisModeMedianMeanRangeStandard DeviationDescriptive MeasuresData VisualizationNumerical AnalysisMeasures of Spread