Math 119 Chapter 3 part 2
TLDRThis instructional video script covers statistical concepts including mean, median, mode, mid-range, and standard deviation. It explains how to calculate the mean and median of a dataset, emphasizing the median's resistance to outliers. The script also discusses the mode, mid-range, and how to estimate the mean from a frequency distribution. It further delves into calculating the standard deviation and variance, illustrating the process both manually and using a calculator, highlighting their significance in measuring data spread and sensitivity to outliers.
Takeaways
- 🔢 The script begins with an example of calculating the mean (mu) for the entire American League's home runs, emphasizing the use of correct notation and the process of summing and dividing by the number of teams.
- 📊 It then moves on to finding the sample mean (x bar) for a simple random sample of five teams, illustrating the process of averaging the home runs of the selected teams and comparing it to the population mean.
- 🤔 The script discusses the representativeness of the sample, noting that the sample mean closely matches the population mean, which is a good sign of representativeness.
- 🏠 The median is introduced as a measure of central tendency that is resistant to outliers and skewness, with an explanation of how to calculate it for both odd and even numbers of observations.
- 📝 The process of finding the median is demonstrated with an example, showing how to arrange data in ascending order and locate the middle value or average the two central values when necessary.
- 📉 The script highlights the difference between the mean and median in the context of skewed distributions, explaining that the median is less influenced by outliers and may provide a better estimate of the center of the data.
- 📊 The mode is mentioned as another measure of central tendency, defined as the most frequently occurring value in a data set, with an example provided to illustrate how to determine the mode.
- 🔢 The mid-range is discussed as a simple measure of central tendency that is sensitive to outliers, calculated as the average of the maximum and minimum values.
- 📈 The script covers the calculation of the mean from a frequency distribution, using midpoints to estimate the mean when exact values are not provided.
- 📊 Weighted mean is introduced, explaining how to calculate the mean of scores that are weighted differently, such as exams contributing different percentages to a final grade.
- 📚 The importance of measures of variation such as range, standard deviation, variance, and quartiles is emphasized, with a focus on standard deviation as a key tool in understanding data spread.
Q & A
What was the issue with the previous video that the speaker mentioned at the beginning?
-The speaker mentioned that in the last video, they lost connection and therefore had to start over with the example they were discussing.
What is the notation used for the population mean in the script?
-The speaker uses 'mu' (μ) to denote the population mean.
How many home runs did the American League have on average according to the script?
-The average number of home runs for the entire American League was calculated to be 179.
What is the symbol used to represent the sample mean in the script?
-The sample mean is represented by 'x bar' in the script.
What was the calculated sample mean of home runs for the five randomly chosen teams?
-The calculated sample mean (x bar) for the five randomly chosen teams was 179.8 home runs.
What does the speaker suggest about the representativeness of the sample in the American League?
-The speaker suggests that the sample is quite representative of the American League since the sample mean of 179.8 is close to the population mean of 179.
What is the definition of the median according to the script?
-The median is defined as the midpoint or middle value of a distribution, such that half of the observations are smaller and the other half are larger.
How is the median calculated for an even number of observations?
-For an even number of observations, the median is calculated as the mean of the two middle observations in the ordered list.
What is the formula used to find the location of the median in a dataset?
-The formula used to find the location of the median is (n + 1) / 2, where n is the number of observations.
Why is the median considered a resistant measure in statistics?
-The median is considered a resistant measure because it is not influenced by skewness and outliers, making it a more accurate measure of central tendency for skewed distributions or those with outliers.
How does the speaker describe the process of finding the mode in a dataset?
-The speaker describes the mode as the value that occurs most frequently in a dataset. If no value occurs more than any other, there is no mode. If multiple values occur with the same highest frequency, they are all considered modes.
What is the mid-range and how is it calculated?
-The mid-range is a measure of central tendency that is calculated by taking the value midway between the minimum and maximum values of the dataset. It is found by adding the smallest and largest values and dividing by two.
How does the speaker explain the calculation of the mean from a frequency distribution?
-The speaker explains that to calculate the mean from a frequency distribution, you use the midpoints of the intervals for each category, multiply them by their respective frequencies, sum these products, and then divide by the total number of observations.
What is the formula for calculating the weighted mean and how does it differ from a simple mean?
-The formula for calculating the weighted mean involves multiplying each value by its respective weight and then summing these products. It differs from a simple mean by taking into account the different importance or weight of each value. The sum of weights is used as the divisor instead of the number of values.
What are the key measures of variation discussed in the script?
-The key measures of variation discussed in the script are range, standard deviation, variance, and quartiles.
How is the range calculated and what does it indicate?
-The range is calculated by subtracting the minimum value from the maximum value in a dataset. It indicates the spread or dispersion of the data from the lowest to the highest value.
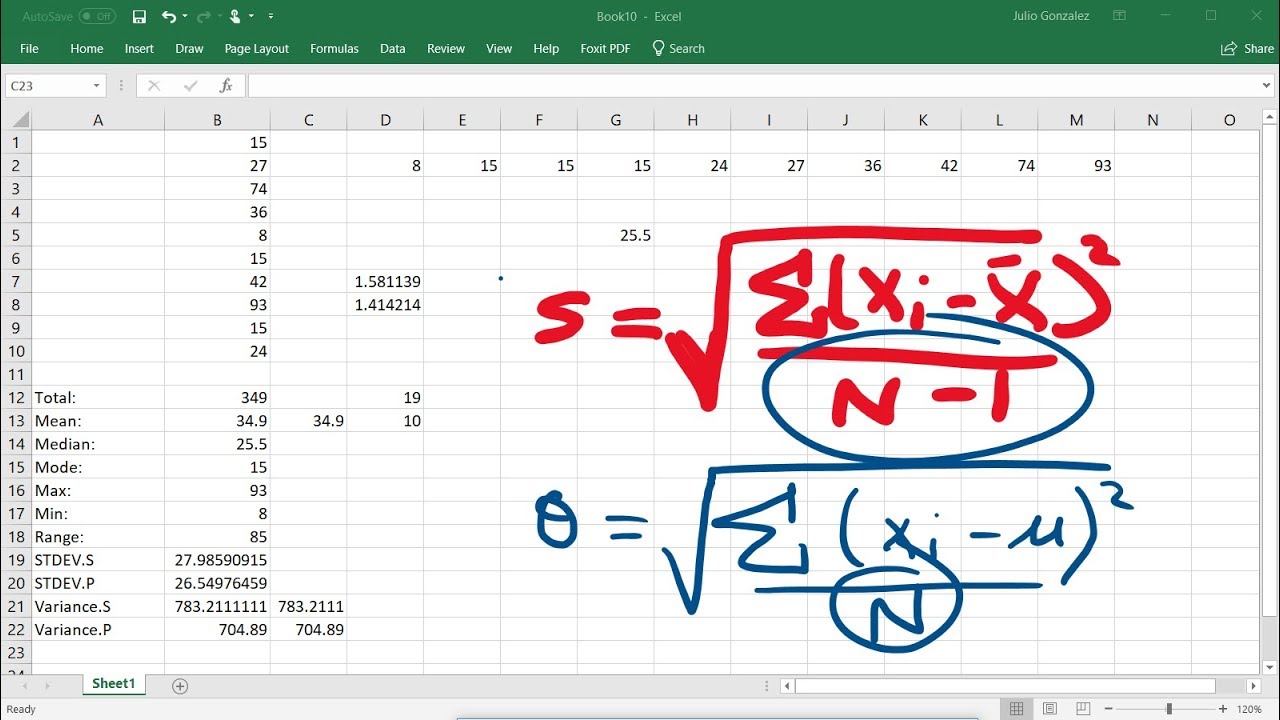
What is the standard deviation and how is it related to variance?
-Standard deviation is a measure that indicates the average variation of data values from their mean. It is related to variance as the square of the standard deviation equals the variance. If you know the variance, you can find the standard deviation by taking its square root, and vice versa.
Why might the standard deviation of a sample tend to underestimate the standard deviation of the population?
-The standard deviation of a sample might tend to underestimate the standard deviation of the population because a sample may not capture the full variability present in the entire population, especially if the sample is not large or representative enough.
What does the speaker suggest about the importance of standard deviation compared to variance?
-The speaker suggests that standard deviation is more important than variance in most practical applications. While variance is mathematically prior to standard deviation in some formulas, the speaker prefers to focus on standard deviation because it is more intuitive and directly interpretable.
Outlines
🏠 Calculating the Mean and Median for Baseball Home Runs
The video script begins with an explanation of calculating the mean number of home runs for the entire American League, using the Greek letter mu (μ) to represent the population mean. The presenter adds up the home runs for all teams and divides by the number of teams to find the average. A sample mean (x̄) is then calculated for a simple random sample of five teams, resulting in a close approximation to the population mean. The script also introduces the concept of the median as a measure of central tendency and explains the difference between calculating the median for odd and even numbers of observations.
📊 Understanding Median and Mean in Data Analysis
This paragraph delves deeper into the concepts of median and mean, emphasizing the median's resistance to skewness and outliers. The presenter provides an example of recalculating the median after replacing measurements of lead and explains how the median is found for both odd and even numbers of data points. The script also discusses the median's utility in skewed distributions and the use of a graphing calculator to find mean and median quickly, including a demonstration of how to input data into a calculator and retrieve statistical measures.
🔢 Mean, Median, and Mode in Statistical Analysis
The script continues with a discussion on the mean as a measure of central tendency, comparing it to the median and mode. It explains how the mean can be skewed by outliers, while the median provides a more accurate representation of the center of data in such cases. The mode, which is the most frequently occurring value in a data set, is also introduced, along with the concept of the mid-range, which is the midpoint between the maximum and minimum values of a data set. The presenter highlights the sensitivity of the mid-range to outliers.
📈 Exploring the Impact of Outliers on Mean and Median
This section provides an example of weight gain during pregnancy to illustrate the impact of outliers on the mean and median. The presenter calculates both the mean and median for the given data, showing that the median is less affected by an outlier (a significantly high weight gain value) and thus may be a better indicator of the center of the data. The script emphasizes the importance of considering the mean and median in the context of data distribution and the presence of outliers.
📊 Mean Calculation from Frequency Distributions
The script addresses the challenge of calculating the mean from a frequency distribution, where specific data points are not provided. The presenter explains how to use the midpoints of the given intervals to approximate the mean by multiplying the midpoint by the frequency of each interval and summing these products, then dividing by the total number of observations. This method allows for estimating the average speed of drivers in a speed trap scenario, despite not having exact speed measurements for each individual.
🎓 Weighted Mean and its Application in Grading
This paragraph introduces the concept of a weighted mean, which is used in scenarios such as grading systems where different exams have different weights. The presenter demonstrates how to calculate a weighted mean by assigning weights to individual exam scores, multiplying each score by its respective weight, summing these products, and then dividing by the sum of the weights. The example given shows how to determine a final course grade based on three exams with varying importance.
📉 Introduction to Measures of Variation in Statistics
The script shifts focus to measures of variation, which describe the dispersion or spread of data. It introduces the range as a simple measure of spread, the standard deviation as a measure of average variation from the mean, and variance as the square of the standard deviation. The presenter explains the process of calculating standard deviation by hand and mentions that it can also be found using a calculator. The importance of understanding variation in data analysis is highlighted, as it provides insights into the consistency and reliability of data.
⚖️ Calculating Standard Deviation and Variance
This section provides a detailed explanation of how to calculate standard deviation and variance, emphasizing their significance in understanding data spread. The presenter demonstrates the steps for calculating standard deviation by hand, including finding the mean, subtracting the mean from each data point, squaring the differences, summing the squares, dividing by the number of observations minus one, and taking the square root of the result. Variance is then explained as the square of the standard deviation, and the relationship between the two is clarified.
🔍 Interpreting Standard Deviation in Real-World Data
The final paragraph of the script discusses the application of standard deviation in analyzing real-world data, such as the amount of sugar in different cereals. The presenter uses a calculator to find the mean, standard deviation, and variance for a given sample of cereals, explaining the process and the significance of each statistical measure. The script concludes with a discussion on the relationship between sample standard deviation and population standard deviation, noting that sample standard deviation is generally a slight underestimate of the population value.
Mindmap
Keywords
💡Mean
💡Population and Sample
💡Median
💡Mode
💡Mid-range
💡Range
💡Standard Deviation
💡Variance
💡Outliers
💡Skewness
Highlights
Introduction to the process of calculating the mean for the entire American League using correct notation.
Explanation of the difference between population mean (mu) and sample mean (x-bar).
Demonstration of calculating the mean for a sample of five baseball teams.
Discussion on the representativeness of a sample compared to the entire population.
Introduction to the concept of the median as a measure of central tendency.
Clarification on the formula for finding the median's location in a dataset.
Process of recalculating the median when measurements are replaced in a dataset.
Explanation of the median's resistance to skewness and outliers in a distribution.
Comparison of the median and mean as estimators of the center of data.
Tutorial on using a graphing calculator to find mean, median, and standard deviation.
Illustration of how the mean can be skewed by outliers in a dataset.
Introduction to the mode as a measure of the most frequently occurring value in a dataset.
Explanation of the mid-range as a measure of central tendency and its sensitivity to outliers.
Demonstration of finding the mid-range and its limitations in a given dataset.
Method for calculating the mean from a frequency distribution using midpoints.
Introduction to weighted mean and its application in calculating test scores.
Overview of measures of variation, including range, standard deviation, variance, and quartiles.
Description of the standard deviation as a measure of average variation from the mean.
Process of calculating standard deviation by hand and using a calculator.
Properties of standard deviation and variance, including their sensitivity to outliers.
Conclusion of the video with a summary of the covered topics and预告of the next video.
Transcripts
Browse More Related Video

Elementary Statistics - Chapter 3 Describing Exploring Comparing Data Measure of Central Tendency

Mode, Median, Mean, Range, and Standard Deviation (1.3)
Calculating The Standard Deviation, Mean, Median, Mode, Range, & Variance Using Excel

Elementary Stats Lesson #3 A

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

How to Find the Standard Deviation, Variance, Mean, Mode, and Range for any Data Set
5.0 / 5 (0 votes)
Thanks for rating: