Lesson 10 - Parametric Equations (Calculus 2 Tutor)

Math and Science
18 Aug 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis section of the advanced calculus tutorial introduces parametric equations, a concept that may seem unfamiliar but is highly useful in real-world applications like engineering and physics. The instructor explains that while parametric equations are not frequently used, they are incredibly powerful when needed. Traditionally, a curve is represented by a function where Y (f(X)) is determined by X. However, parametric equations offer an alternative approach where both X and Y are expressed as functions of a third variable T, called the parameter. This method allows for a different perspective on the relationship between X and Y, making it a valuable tool in certain complex problem-solving scenarios.

Takeaways
  • 📚 Parametric equations are a topic in advanced calculus that might seem unfamiliar at first but are powerful when needed.
  • 🔍 The script explains that while parametric equations are not commonly used, they are essential for certain applications in real-life scenarios like engineering and physics.
  • 📈 A curve can traditionally be represented by a function where Y is a function of X (Y = f(X)), which is a fundamental concept in algebra.
  • 📉 In parametric equations, instead of having Y directly depending on X, both X and Y are expressed as functions of a third variable T, making T the new independent variable.
  • 👉 The term 'parameter' comes from the use of the variable T, which is why the equations are called 'parametric equations'.
  • 🔑 The parameter T allows for a different way of representing the relationship between X and Y, offering flexibility in how functions can be written and understood.
  • 🤔 The script suggests that understanding parametric equations can be challenging because they represent a shift from the traditional function representation.
  • 📚 The importance of parametric equations is highlighted by stating that when they are needed, they are 'really needing bad', indicating their critical role in specific problems.
  • 🔄 The tutorial aims to demystify parametric equations by showing that they are not as complex as they might initially seem.
  • 🎯 The script emphasizes that while parametric equations may not be used frequently, knowing how to work with them is valuable for tackling certain complex problems.
  • 📈 The concept of parametric equations is introduced as an alternative method to represent the relationship between variables, which can be particularly useful in certain fields.
Q & A

  • What is the main topic covered in this section of the advanced calculus tutorial?

    -The main topic covered in this section is parametric equations.

  • Why might students find parametric equations confusing at first?

    -Students might find parametric equations confusing because it's a concept they generally haven't encountered until advanced calculus, and they might wonder why it's taught at all.

  • How often are parametric equations used in real-life applications?

    -Parametric equations are not used frequently, but when they are needed, they are extremely powerful and can greatly simplify complex problems in fields like engineering or physics.

  • What is the significance of the term 'parametric' in parametric equations?

    -The term 'parametric' comes from the use of a parameter, which is an independent variable T that both X and Y are functions of, instead of the traditional relationship where Y is a function of X.

  • What is the traditional way of representing a curve in mathematics?

    -Traditionally, a curve is represented by a function where Y is a function of X, denoted as Y = f(X).

  • What is the role of the variable T in parametric equations?

    -In parametric equations, T is the parameter, which is an independent variable that both X and Y are functions of.

  • Why are parametric equations considered powerful when needed?

    -Parametric equations are powerful because they offer a different perspective to represent the relationship between variables, which can simplify complex problems and provide a clearer understanding of the system being studied.

  • How does the concept of parametric equations differ from traditional functions?

    -Parametric equations differ by introducing a parameter T, where both X and Y are expressed as functions of T, rather than having a direct function Y = f(X).

  • What is the basic idea behind the function Y = f(X)?

    -The basic idea is that you input a value for X into the function and get a corresponding value for Y, which can then be plotted on a graph as a point (X, Y).

  • How does the script describe the process of learning about parametric equations in advanced calculus?

    -The script describes it as a topic that might initially seem unnecessary or confusing, but it emphasizes the importance and utility of parametric equations when they are needed for specific applications.

  • What is the role of the parameter T in the context of parametric equations?

    -The parameter T serves as an independent variable that allows for the representation of both X and Y as functions of T, thus providing a different way to describe the relationship between the variables.

Outlines
00:00
📚 Introduction to Parametric Equations

This paragraph introduces the concept of parametric equations in the context of advanced calculus. The speaker explains that while parametric equations are not commonly used, they are extremely powerful when needed, particularly in fields like engineering and physics. The paragraph clarifies that parametric equations are a way to represent a curve differently from the traditional function of y = f(x). It sets the stage for a deeper dive into how parametric equations work and their significance in various real-life applications.

Mindmap
Keywords
💡Parametric Equations
Parametric equations are a mathematical representation of a curve where both x and y coordinates are expressed as functions of a third variable, typically denoted as 't'. In the context of the video, parametric equations are introduced as a powerful tool in fields like engineering and physics, despite their infrequent use. The video emphasizes their utility when needed, suggesting that they offer a unique perspective for solving complex problems by allowing variables x and y to be dependent on a parameter 't'.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs, with the property that each input is related to exactly one output. In the video, the function is initially introduced as 'y = f(x)', which is a common way to represent a curve where 'y' is determined by the value of 'x'. This concept is fundamental to understanding how parametric equations later diverge from this traditional function by introducing a parameter 't'.
💡Curve
A curve, in the context of the video, refers to the graphical representation of a mathematical relationship, typically between two variables. The video script discusses how a curve can be represented by a function, which is a fundamental concept in algebra and calculus. The introduction of parametric equations offers an alternative way to represent curves, where the relationship between x and y is not direct but mediated through a parameter 't'.
💡Variable
In mathematics, a variable represents a value that can change within certain bounds. The video script uses 'x' and 'y' as variables that define points on a curve. When discussing parametric equations, 'x' and 'y' become functions of another variable 't', which is the parameter. This shift in how variables are treated is key to understanding the parametric form of equations.
💡Parameter
The parameter 't' in parametric equations is an independent variable that dictates the values of 'x' and 'y'. It is the driving force behind the curve's representation in parametric form. The video script explains that 't' is a new variable introduced to create a different perspective on the relationship between 'x' and 'y', making it a central concept in understanding parametric equations.
💡Engineering
Engineering is a professional discipline that applies scientific principles to design, build, and maintain structures, machines, devices, and systems. The video mentions engineering as one of the fields where parametric equations can be particularly useful. This implies that parametric equations can provide solutions or insights in real-world applications that are common in engineering problems.
💡Physics
Physics is a natural science that studies matter, energy, and the fundamental forces of nature. The video script highlights physics as another field where parametric equations can be beneficial. This suggests that the equations can model and analyze physical phenomena where the relationship between variables is best represented through a parameter.
💡Algebra
Algebra is a branch of mathematics concerning the study of symbolic manipulations and the solving of equations. The video script refers to algebra when discussing the basic understanding of functions and variables. It uses algebraic concepts to build up to the more advanced topic of parametric equations, showing the progression from simple algebraic principles to the complexities of calculus.
💡Calculus
Calculus is a branch of mathematics that deals with the study of change and motion, and it is typically where students first encounter parametric equations. The video script positions calculus as the advanced study area where parametric equations are introduced, indicating that these equations are part of a more complex mathematical framework.
💡Graph
A graph is a visual representation of data, typically with coordinates on a plane. In the video, the concept of plotting points on a graph is used to illustrate how functions yield curves. The script mentions that by plugging values into a function, one can obtain points (x, y) that can be graphed, which is a basic principle in understanding how parametric equations also result in graphical representations of curves.
Highlights

Introduction to the topic of parametric equations in advanced calculus.

Parametric equations are not commonly used but are powerful when needed in real-life applications such as engineering or physics.

Parametric equations are taught in calculus despite their infrequent use due to their utility in specific scenarios.

A curve can traditionally be represented by a function where Y is a function of X.

Parametric equations offer a different way to represent the relationship between variables.

In parametric equations, both X and Y are functions of a new variable T, which is the parameter.

The parameter T allows for a more flexible representation of curves.

Parametric equations can be used to represent any function.

The variable T is the independent variable in parametric equations.

The concept of dependent and independent variables is revisited with the introduction of T.

Parametric equations shift the dependency from Y on X to both X and Y on T.

The simplicity of parametric equations lies in their ability to describe complex curves with a single parameter.

Parametric equations are particularly useful in dynamic systems where time or another variable is a key factor.

Understanding parametric equations enhances problem-solving skills in calculus.

Parametric equations can simplify the visualization and analysis of complex mathematical models.

The tutorial aims to demystify parametric equations and show their practical applications.

The importance of recognizing when to use parametric equations in problem-solving.

A step-by-step guide on how to convert standard functions into parametric equations.

Transcripts

Browse More Related Video

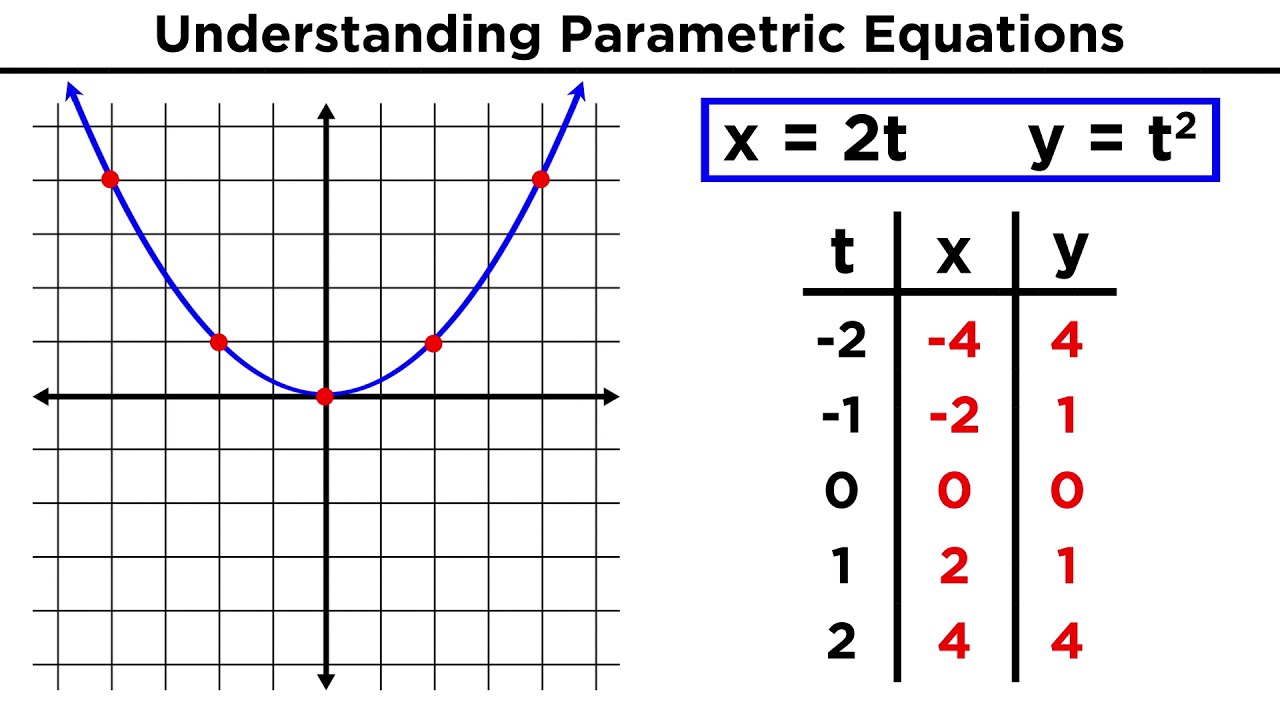
Parametric Equations

Ch. 8.4 Plane Curves and Parametric Equations

Parametric equations 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy

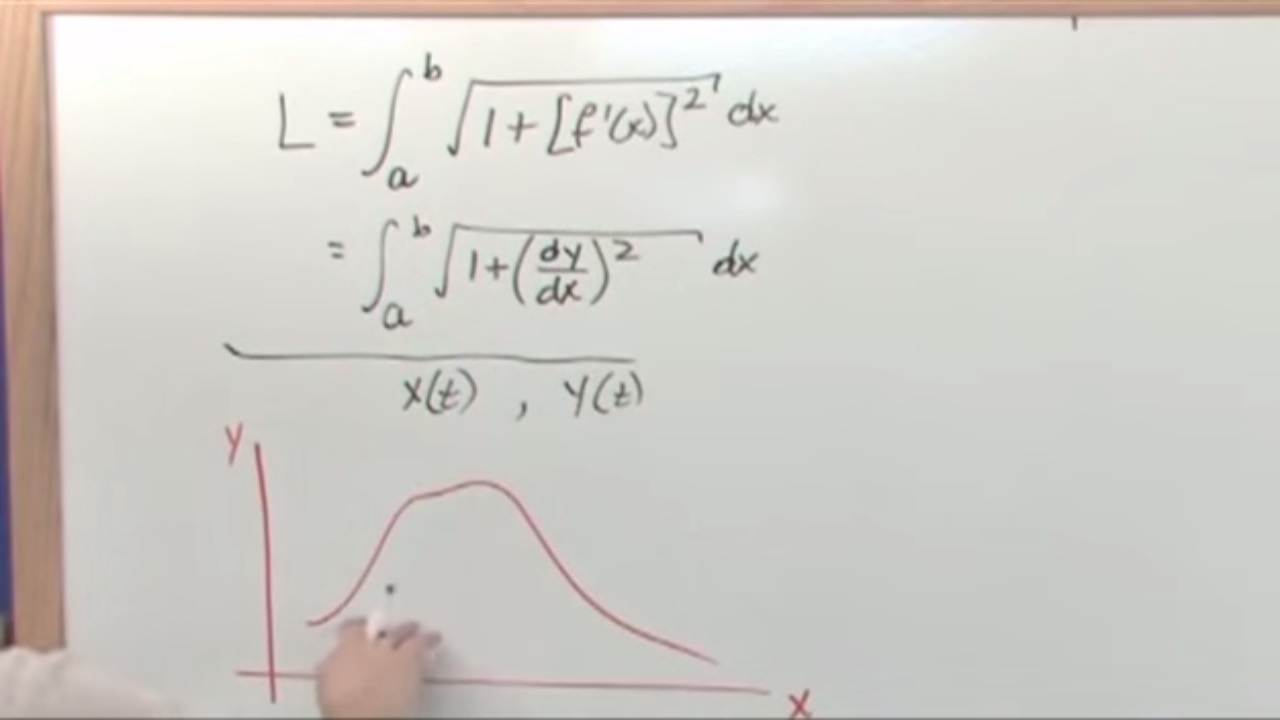
Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

AP Calculus BC Lesson 9.1

Parametric equations 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Parametric EquationsAdvanced CalculusReal-Life ApplicationsEngineeringPhysicsMathematicsFunction RepresentationAlgebra BasicsCurve AnalysisEducational Tutorial