AP Calculus BC Lesson 9.1
TLDRThis lesson introduces parametric equations, involving three variables, where 'T' is the parameter used to calculate 'X' and 'Y'. The video demonstrates how to graph parametric equations by plugging in different 'T' values and connecting the resulting points to form a curve. It also explains how to find the derivatives of parametric equations using the formula dy/dx = dy/dt / dx/dt, which is crucial for determining the slope of the tangent lines at specific points on the curve. The lesson further explores scenarios leading to horizontal and vertical tangents and provides solutions to multiple-choice questions related to parametric equations and their derivatives.
Takeaways
- 📚 Parametric equations involve three variables, typically x, y, and a parameter T.
- 📈 To graph parametric equations, substitute different values for T into the equations to find corresponding (x, y) points and connect them to form a curve.
- 📊 The graphing calculator can be used to graph parametric equations by switching to parametric mode and inputting X(t) and Y(t) functions.
- 🌐 The parameter T is used to calculate X and Y and represents a third variable in parametric equations.
- 🔄 Parametric equations allow determining the XY position of a particle in a coordinate plane at a given time.
- 🎓 The derivatives of parametric equations are found using the formula dy/dx = (dy/dt) / (dx/dt), assuming dx/dt ≠ 0.
- 🏞️ Horizontal tangent lines occur when dy/dt = 0, and vertical tangent lines occur when dx/dt = 0.
- 🧮 To find the slope of the tangent line at a specific T value, calculate dy/dx by dividing dy/dt by dx/dt at that T.
- 🌟 The T value for a vertical tangent in a parametric curve is found by setting dx/dt to zero and solving for T.
- 🛤️ The slope of the tangent line to a parametric curve at a given T can be used to write the equation of the tangent line in point-slope form.
Q & A
What are parametric equations and how do they involve three variables?
-Parametric equations are a set of equations that describe the path of a moving point in a coordinate plane. They involve three variables: x, y, and usually a third variable, often denoted as T or u. The x and y coordinates are expressed as functions of the third variable, which is used to calculate the position of a particle at a given time.
How can you determine if a set of parametric equations is continuous on a closed interval?
-A set of parametric equations X(T) and Y(T) is considered continuous on a closed interval from A to B if both functions are continuous for all values of T within that interval. This means there are no breaks or jumps in the curve defined by the equations over the given range of T.
What is the process for graphing a curve defined by parametric equations?
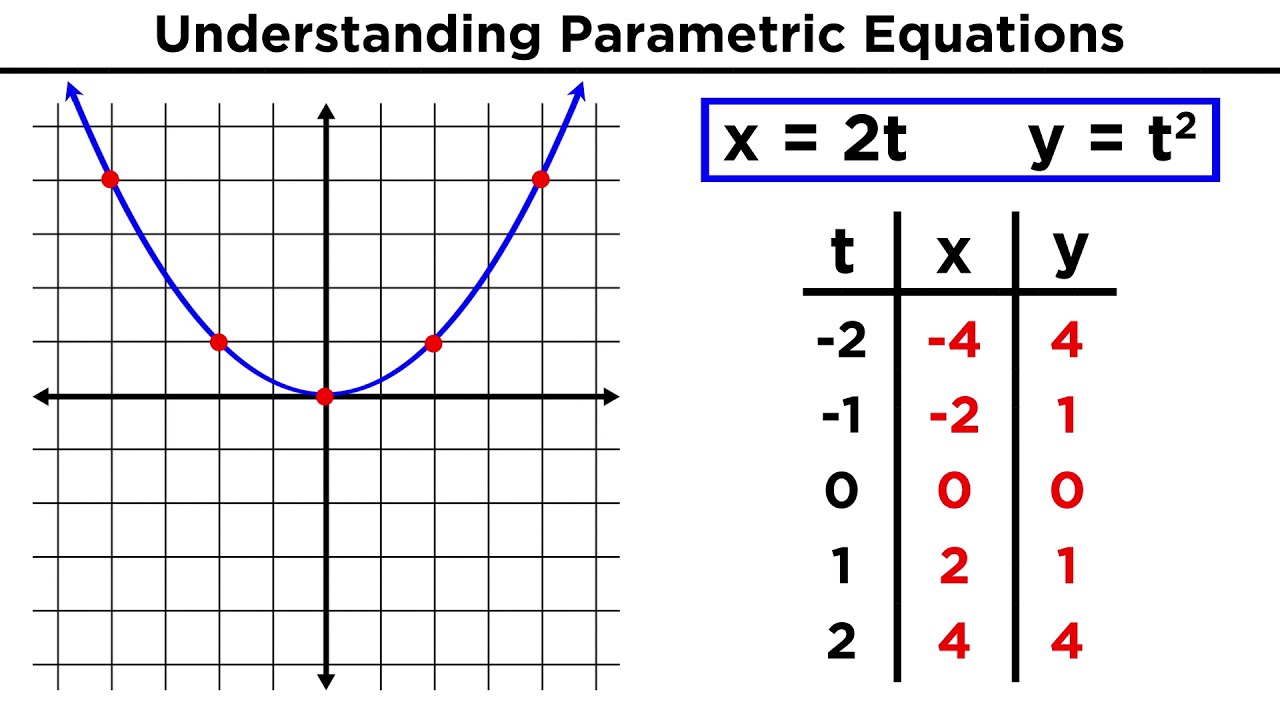
-To graph a curve defined by parametric equations, you plug in different values for the parameter T into the equations for x and y. This generates a set of (x, y) points. You then plot these points on the coordinate plane and connect them with a smooth curve to visualize the shape defined by the parametric equations.
How can you find the derivatives of parametric equations?
-To find the derivatives of parametric equations, you use the formula dy/dx = (dy/dt) / (dx/dt). Here, dy/dt and dx/dt are the derivatives of the y and x functions with respect to the parameter T, respectively. This formula gives you the slope of the tangent line to the curve at any point, which is equivalent to the derivative in the standard sense.
What are the conditions for a parametric curve to have a horizontal tangent line?
-A parametric curve has a horizontal tangent line when the numerator of its derivative (dy/dt) is equal to zero. This means that the rate of change in y with respect to time (T) is zero at the point of tangency.
What are the conditions for a parametric curve to have a vertical tangent line?
-A parametric curve has a vertical tangent line when the denominator of its derivative (dx/dt) is equal to zero. This situation leads to an undefined slope, as you are dividing by zero, which indicates a sharp turn or a vertical tangent at that point.
How can you use a graphing calculator to graph parametric equations?
-To graph parametric equations using a graphing calculator, you switch the calculator to parametric mode. You then enter the parametric equations for x and y in terms of the parameter T. The calculator will graph the curve starting from T equals zero, as negative time values are typically not considered.
What is the significance of the parameter T in parametric equations?
-The parameter T in parametric equations is the independent variable that is used to calculate the dependent variables x and y. It represents the time or some other parameter that varies in a system, and it is what you change to trace the path of the curve in the coordinate plane.
How do you find the slope of the tangent line to a parametric curve at a specific point?
-To find the slope of the tangent line to a parametric curve at a specific point, you calculate the derivative of y with respect to x (dy/dx) at that point. Since parametric equations are in terms of a third variable T, you actually calculate dy/dt and dx/dt and then find the ratio (dy/dt) / (dx/dt) at the specific value of T.
What happens when DX/DT is zero in parametric equations?
-When DX/DT is zero in parametric equations, it indicates that there is a vertical tangent line at that point. This is because the denominator of the derivative dy/dx (which is actually dy/dt over dx/dt) becomes zero, leading to an undefined slope and thus a vertical tangent line.
How do you interpret the restriction T being greater than zero in parametric equations?
-The restriction that T be greater than zero in parametric equations typically means that the domain of the parameter T is restricted to positive values only. This could be due to physical or mathematical constraints of the problem, such as representing time where negative values would not make sense.
Outlines
📚 Introduction to Parametric Equations
The video begins with an introduction to parametric equations, explaining that they involve three variables: x, y, and a third variable often represented as t (parameter). The concept is illustrated with an example where X(t) = 3t^2 and Y(t) = t - 2, showing how to calculate the (x, y) coordinates for a given t value. It emphasizes that if X(t) and Y(t) are continuous on a closed interval [A, B], they form valid parametric equations. The video then demonstrates how to graph these equations by plotting points for various t values and connecting them to form a curve. Additionally, the video introduces how to use a graphing calculator in parametric mode to visualize such equations.
📈 Calculating Tangent Lines and Derivatives
This paragraph delves into the process of finding the slope of the line tangent to the graph of a parametric curve at a specific point. It explains the concept of parametric derivatives using the formula dy/dx = (dy/dt) / (dx/dt). The video provides examples of calculating tangent lines for different parametric equations, emphasizing how to find the derivative with respect to t and evaluate it at particular t values to get the slope. It also discusses the conditions for horizontal and vertical tangent lines, explaining that horizontal tangents occur when dy/dt is zero and vertical tangents occur when dx/dt is zero.
🔢 Solving Parametric Equations for Tangent Lines
The paragraph focuses on solving parametric equations to find the equations of tangent lines at specific points. It presents multiple-choice questions related to finding the slope and equation of tangent lines for different parametric equations. The solutions involve taking derivatives with respect to t, plugging in specific t values to find the coordinates of the point of tangency, and then using these to determine the slope and the equation of the tangent line. The video also highlights the importance of considering the domain restrictions of the parameter t when solving these problems.
🌐 Applications of Parametric Equations in Motion
The final paragraph discusses the application of parametric equations in describing the motion of a particle in the XY plane. It introduces a scenario where a particle moves such that its position is given by parametric equations involving functions of time t. The video then demonstrates how to find the slope of the tangent line to the path of the particle at a given time by calculating the derivatives dx/dt and dy/dt and using them to find the slope dy/dx at that specific time. The example provided involves the particle's motion described by X(t) = 4sin(t) and Y(t) = (2 + t^2)ln(t), with the slope of the tangent line at t = 4 being calculated to be 0.701.
Mindmap
Keywords
💡Parametric Equations
💡Derivatives
💡Graphing
💡Tangent Lines
💡Graphing Calculator
💡Slope
💡Continuous Functions
💡Coordinate Plane
💡Particle Motion
💡Rate of Change
Highlights
Defining parametric equations as a way to determine the X Y position of a particle at a given time.
Parametric equations involve three variables: x, y, and a parameter T.
Graphing curves defined by parametric equations by plugging in different values for T.
If x(T) and y(T) are continuous on a closed interval [A, B], the equations are considered valid parametric equations.
Using a graphing calculator in parametric mode to graph equations like x(T) = 3T^2 and y(T) = T - 2.
Parametric equations typically start at T=0 on the AP exam and T ≥ 0.
Derivatives of parametric equations are found using the formula dy/dx = dy/dt / dx/dt.
Horizontal tangent lines occur when dy/dt = 0.
Vertical tangent lines occur when dx/dt = 0.
Slope of the tangent line to a curve defined by parametric equations X(T) = e^T and Y(T) = T^2 + 5 at T=3 is found by calculating dy/dx using the given formula.
Equation of the tangent line to a curve defined by X(T) = 2T^3 - T^2 and Y(T) = T^4 at T=2 involves finding the point (12, 16) and the slope 32/20 or 8/5.
For a curve defined by X(T) = 5T and Y(T) = T^2 - 1, the equation of the tangent line at T=1 is Y = (2/5)x - 2.
Curve defined by X(T) = 4T^4 - T^2 and Y(T) = cos(2T) has a vertical tangent at T = 1/√8 because DX/DT = 0 at this point.
Curve defined by X(T) = 5e^T and Y(T) = 3T^3 - 4T has a horizontal tangent at T = ±√4/√9, and a vertical tangent at T = ±√2.
For a particle moving along a curve with dX/DT = √(1 + T^2) and dY/DT = ln(2 + T^2), the slope of the tangent line at T=4 is approximately 0.701.
Parametric equations allow for the representation of curves and motion in a 2D plane using a third parameter, T.
The parameter T is used to calculate the X and Y coordinates for a given point on a curve.
Graphing parametric equations helps visualize the curve and understand the motion of a particle.
Understanding when horizontal or vertical tangents occur is crucial for analyzing the behavior of parametric curves.
The process of finding the slope of the tangent line to a parametric curve involves calculating the derivatives with respect to T and then evaluating at a specific T value.
The concept of parametric equations extends to various applications, including physics and engineering, where it can model the motion of objects.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: