Parametric equations 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy
TLDRThe video script explores the process of eliminating the parameter 't' from parametric equations involving trigonometric functions. It starts with the equations x = 3cos(t) and y = 2sin(t), aiming to remove 't' to find a more intuitive relationship between x and y. The instructor initially demonstrates a direct substitution method leading to a complex answer, then introduces a trigonometric identity to simplify the equations into the standard form of an ellipse, x²/9 + y²/4 = 1. The script also discusses the importance of understanding the direction of motion in parametric equations and illustrates this by plotting points for different values of 't', showing the counterclockwise path of an object in motion. The video concludes by emphasizing the clarity gained by converting parametric equations into a recognizable geometric form.
Takeaways
- 📚 The video discusses the process of eliminating the parameter 't' from parametric equations involving trigonometric functions.
- 🔍 Initially, the instructor attempts to remove 't' by solving for 't' in terms of 'x' or 'y', resulting in a complex and unintuitive equation.
- 📉 The instructor emphasizes the importance of understanding the difference between 'arcsine' and 'inverse sine' to avoid confusion with exponentiation.
- 📐 The video introduces a trigonometric identity, \( \cos^2(t) + \sin^2(t) = 1 \), which is key to simplifying the parametric equations.
- 🔑 By substituting \( x/3 \) for \( \cos(t) \) and \( y/2 \) for \( \sin(t) \), the equations are simplified to an equation of an ellipse, \( x^2/9 + y^2/4 = 1 \).
- 📈 The simplified equation is recognized as representing an ellipse, which is easier to visualize and understand compared to the original parametric form.
- 📊 The video demonstrates how to graph the ellipse by identifying the semi-major and semi-minor axes from the simplified equation.
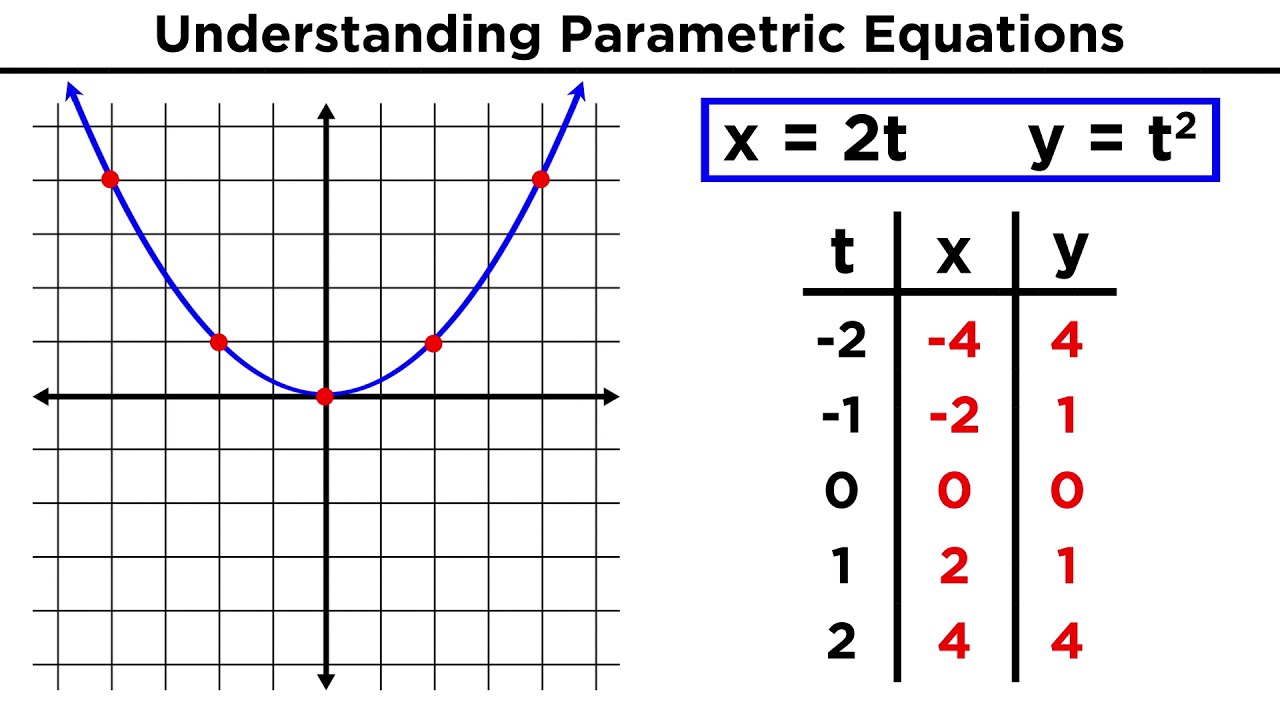
- 📍 The instructor creates a table to show the values of 'x' and 'y' for different values of 't', helping to understand the motion described by the parametric equations.
- 📈 By plotting points for specific 't' values, the direction of motion (counterclockwise) is determined for the parametric equations.
- 🔁 The video concludes by discussing how varying 't' from 0 to infinity would result in tracing the ellipse multiple times.
- 🔍 Finally, the video hints at the connection between the parametric equations and polar coordinates, suggesting further exploration for a deeper understanding.
Q & A
What is the purpose of the video script?
-The purpose of the video script is to demonstrate how to remove the parameter 't' from a set of parametric equations involving trigonometric functions and to show that the resulting equation describes an ellipse.
What are the initial parametric equations given in the script?
-The initial parametric equations are x = 3 * cos(t) and y = 2 * sin(t).
Why does the script mention the potential confusion between 'arcsine' and 'inverse sine'?
-The script mentions the potential confusion because 'inverse sine' can be misinterpreted as taking the sine of a number to the power of -1, whereas 'arcsine' clearly indicates the inverse function of sine.
What trigonometric identity is used to eliminate the parameter 't'?
-The trigonometric identity used to eliminate the parameter 't' is cos^2(t) + sin^2(t) = 1.
How does the script simplify the parametric equations to an equation of an ellipse?
-The script simplifies the parametric equations by substituting x/3 for cos(t) and y/2 for sin(t) in the trigonometric identity, resulting in the equation x^2/9 + y^2/4 = 1, which is the standard form of an ellipse.
What does the script suggest about the direction of motion if the parametric equations describe a particle in motion?
-The script suggests that by plotting points for different values of 't', one can determine the direction of motion. In this case, the direction is counterclockwise as 't' increases from 0 to 2π.
What is the significance of the points (3,0), (0,2), and (-3,0) in the script?
-These points are significant because they represent the position of a particle at specific values of 't' (0, π/2, and π, respectively) and help to determine the direction of motion as well as confirm the shape of the ellipse.
How does the script relate the parametric equations to polar coordinates?
-The script relates the parametric equations to polar coordinates by suggesting that 't' could represent the angle in polar coordinates and by mentioning that the process touches on concepts that are explained in videos about polar coordinates.
What is the script's explanation for why three points are needed to determine the direction of motion?
-The script explains that three points are needed because two points alone could suggest a different direction if the particle were to move in the opposite way around the ellipse.
What does the script imply about the process of eliminating the parameter 't'?
-The script implies that eliminating the parameter 't' can lead to a more intuitive understanding of the shape described by the parametric equations, but it may also result in losing information about the direction of motion and the specific position at any given time 't'.
Outlines
📚 Removing Parameters from Parametric Equations
The paragraph introduces the process of eliminating a parameter 't' from parametric equations. It uses the example where x = 3cos(t) and y = 2sin(t). The speaker explains that solving for 't' and substituting back can lead to a complex and unintuitive answer. The paragraph also clarifies the difference between 'arcsine' and 'inverse sine' to avoid confusion, emphasizing the importance of correct notation in trigonometry.
📈 Transforming Parametric Equations into an Ellipse
This section focuses on transforming the given parametric equations into a more intuitive form, specifically an ellipse equation. By dividing the original equations by their respective constants, the speaker derives x/3 = cos(t) and y/2 = sin(t). Using the trigonometric identity cos^2(t) + sin^2(t) = 1, the equations are simplified to x^2/9 + y^2/4 = 1, which is recognized as the standard form of an ellipse equation. The paragraph also includes a step-by-step explanation of how to graph the ellipse and the significance of the major and minor axes.
📊 Plotting Points to Determine Motion Direction
The final paragraph discusses the importance of plotting points to understand the motion described by the parametric equations. By selecting specific values of 't' and calculating the corresponding x and y values, the speaker demonstrates how to plot points on the ellipse and deduce the direction of motion (counterclockwise in this case). The paragraph also touches on the implications of different 't' ranges on the number of times the ellipse is traced and concludes with a reflection on the journey from parametric equations to a clear geometric representation.
Mindmap
Keywords
💡Polynomial Equations
💡Parametric Equations
💡Trigonometric Identities
💡Unit Circle
💡Arcsine
💡Ellipse
💡Semi-major Axis
💡Semi-minor Axis
💡Conic Sections
💡Polar Coordinates
Highlights
Attempt to remove parameter 't' from a parametric equation involving cosine and sine functions.
Parametric equations given as x = 3cos(t) and y = 2sin(t).
Solving for 't' in terms of 'x' or 'y' to eliminate the parameter.
Demonstration of an unintuitive method to eliminate 't' leading to a complex equation.
Clarification on the use of 'arcsine' versus 'inverse sine' to avoid confusion.
Explanation of the difference between 'arcsine(y)' and 'sine(y)^-1'.
Introduction to the trigonometric identity involving cosine squared plus sine squared equals one.
Strategy to replace trigonometric expressions with expressions in 'x' and 'y'.
Transformation of parametric equations into a form that resembles an ellipse.
Derivation of the simplified equation x^2/9 + y^2/4 = 1 representing an ellipse.
Graphical representation of the ellipse with its semi-major and semi-minor axes.
Loss of information about the direction of motion and position on the ellipse when parameters are removed.
Creation of a table to plot points and understand the direction of motion described by the parametric equations.
Plotting of points to visualize the trajectory of the parametric equations on the ellipse.
Discussion on the implications of different bounds of 't' and their effect on the completeness of the ellipse's traversal.
Connection between the parametric equations and polar coordinates, suggesting further exploration.
Final reflection on the journey from parametric equations to recognizing the shape and motion on an ellipse.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: