Arclength

RH Mathematics
10 May 202106:48
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the concept of arc length, a fundamental topic in calculus BC courses not covered in AP Calculus. The instructor explains that arc length requires a reasonably smooth, rectifiable curve, excluding curves like sine of one over x which become too erratic near the origin. The lesson builds on the Riemann sum, breaking the arc into small segments, adding them up, and eventually transitioning to an integral. The video introduces the arc length formula, \( \sqrt{1 + (dy/dx)^2} \), which is derived by cleverly manipulating the sum of small right triangle hypotenuses, and emphasizes its utility in most problems, often requiring only setup or calculator assistance.

Takeaways
  • πŸ“š Arc length is a topic typically studied in a calculus BC course and is not included in the AP calculus curriculum.
  • πŸ” To find the arc length of a curve, the curve must be continuous and rectifiable, meaning it should be reasonably smooth.
  • πŸ”πŸ” The concept of rectifiability is not deeply explored, but it's implied that most curves encountered will be suitable for arc length calculations.
  • πŸ“ The arc length calculation involves breaking down the curve into small segments and summing the lengths of these segments.
  • πŸ“ˆ The idea of a Riemann sum is used to approximate the total arc length by adding up small pieces of the curve.
  • πŸ‘‰ Each small segment of the curve is considered as a right triangle, with the hypotenuse representing a small piece of the arc length.
  • 🧩 The length of each small segment (delta p) is the square root of the sum of the squares of delta x and delta y.
  • πŸ”’ As delta x approaches zero, the sum of delta ps transforms into an integral, which is a key step in the derivation of the arc length formula.
  • πŸ”„ The formula for arc length involves multiplying by a clever form of one, specifically delta x over delta x, to simplify the expression.
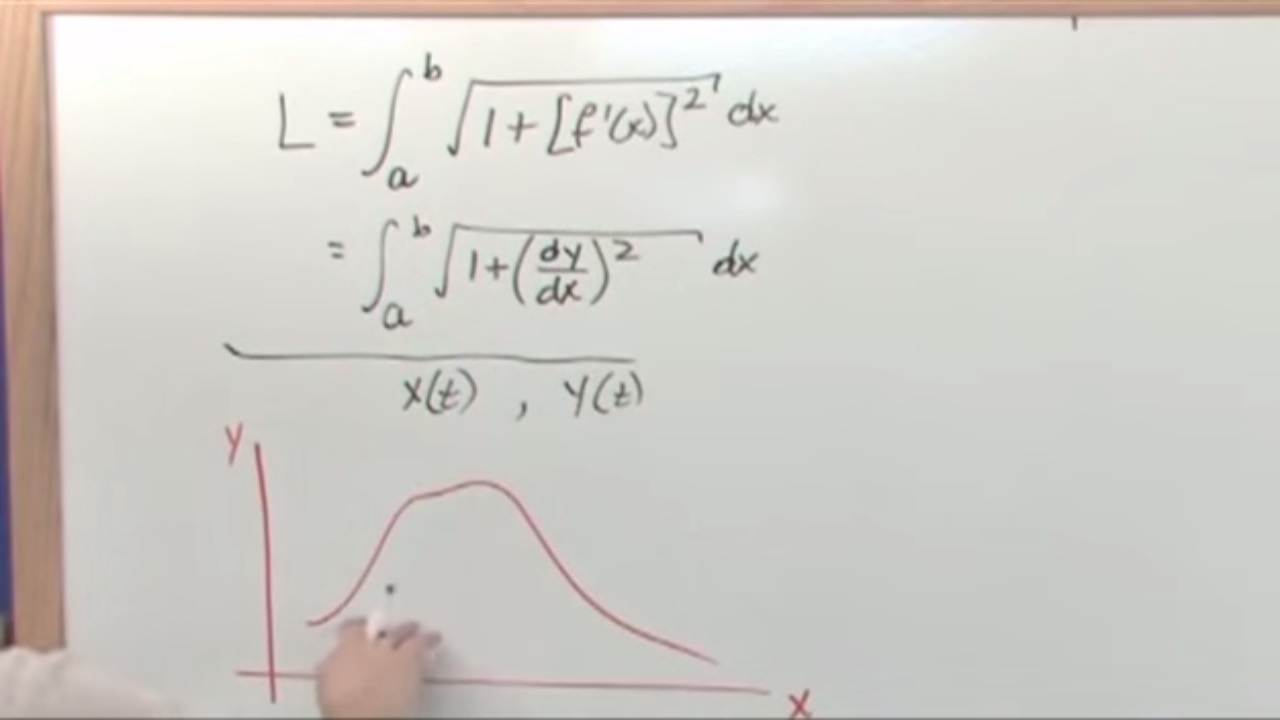
  • πŸ”Ž The final arc length formula is derived as the integral of the square root of (1 + (dy/dx)^2) dx, where dy/dx represents the derivative of y with respect to x.
  • πŸ’‘ The arc length formula is often either a calculator question or a setup question, as it typically does not require manual integration due to its complexity.
Q & A

  • What is the topic discussed in the video?

    -The video discusses the concept of arc length, which is a topic often studied in a calculus BC course.

  • Why is arc length not included in the AP Calculus course?

    -The video does not explicitly state why arc length is not included in the AP Calculus course, but it implies that it might be due to its complexity or the fact that it is a more advanced topic.

  • What does the term 'rectifiable' imply in the context of curves?

    -A rectifiable curve is one that has a finite length. The video mentions that while it won't delve into the specifics of what curves are and aren't rectifiable, most curves encountered in the class will be rectifiable.

  • Why can't the arc length of the sine of one over x be defined on the open interval?

    -The sine of one over x curve gets extremely wiggly towards the origin, making it impossible to define an arc length on the open interval due to its non-rectifiable nature.

  • What is the basic idea behind calculating arc length?

    -The basic idea is to consider small pieces of the arc length, calculate the length of each piece, and then sum them up, which is similar to the concept of a Riemann sum.

  • How is the length of a small piece of arc length related to delta x and delta y?

    -The length of a small piece of arc length, denoted as delta p, is the square root of the sum of the squares of delta x and delta y (i.e., √(Ξ”xΒ² + Ξ”yΒ²)).

  • What is the significance of multiplying by delta x over delta x in the arc length formula?

    -Multiplying by delta x over delta x is a clever way to manipulate the expression to make it more suitable for turning into an integral as delta x approaches zero.

  • Why is the arc length formula represented as an integral?

    -The arc length formula is represented as an integral because it sums up infinitely many small pieces of arc lengths as delta x approaches zero, which is a definition of an integral in calculus.

  • What does the term 'dy/dx' represent in the arc length formula?

    -In the arc length formula, 'dy/dx' represents the derivative of y with respect to x, which is used to describe the rate of change of y as x changes.

  • Why is the arc length formula often a set-it-up-but-don't-evaluate question?

    -The arc length formula is often a set-it-up-but-don't-evaluate question because it usually involves complex expressions that are difficult to integrate directly, requiring either a calculator or an understanding of the setup without the need for full evaluation.

Outlines
00:00
πŸ“š Introduction to Arc Length in Calculus BC

This paragraph introduces the concept of arc length, a fundamental topic in a Calculus BC course, which is not covered in the standard AP Calculus curriculum. The speaker explains that the topic requires a rectifiable curve, meaning it must be reasonably smooth and not overly complex like the sine of one over x, which becomes very wiggly near the origin. The focus is on breaking down the arc into small pieces, each represented by a small delta segment, and summing these to find the total arc length. The method discussed is reminiscent of the Riemann sum, where the length of each small piece is calculated and then aggregated. The speaker also touches on the mathematical process of converting the sum of these small pieces into an integral, emphasizing the need to multiply by a clever form of one to account for the delta x in the denominator and to simplify the expression into a form that can be integrated.

05:04
πŸ“ Deriving the Arc Length Formula

The second paragraph delves into the derivation of the arc length formula. It starts by discussing the transition from summing small delta segments to an integral as the number of pieces approaches infinity and delta x approaches zero. The speaker explains the transformation of the sum of square roots of delta x squared plus delta y squared into an integral, which involves recognizing the need for a clever multiplication by one to simplify the expression. The formula for arc length is then presented as the integral of the square root of one plus the derivative of y with respect to x squared, dx. The paragraph also addresses the practicality of this formula, noting that it is often either a calculator question or a setup without evaluation, and highlights the rarity of cases where the derivative squared plus one forms a perfect square, which would simplify the integration process.

Mindmap
Keywords
πŸ’‘Arc Length
Arc length refers to the distance along a curve, and it is a fundamental concept in calculus, especially in the context of a calculus BC course. In the video, the speaker discusses how to calculate the arc length of a continuous and reasonably smooth curve. The process involves breaking the curve into small segments and summing their lengths, which is closely related to the Riemann sum in calculus.
πŸ’‘Rectifiable
A curve is considered rectifiable if its arc length can be calculated. This term is used to describe curves that are not too complex or irregular, such as those that become extremely wiggly near the origin, like the sine of one over x. The video mentions that most curves encountered in a calculus course will be rectifiable, allowing for the calculation of their arc lengths.
πŸ’‘Riemann Sum
The Riemann sum is a method used in calculus to approximate the definite integral of a function. In the context of the video, the speaker uses the concept of the Riemann sum to explain how to calculate the arc length by summing the lengths of small segments of the curve. This approach is foundational in understanding how to transition from finite sums to integrals in calculus.
πŸ’‘Delta P
In the script, 'delta p' represents a small piece of the curve's arc length. The speaker uses this term to describe the incremental lengths of the curve as they are added together to find the total arc length. This concept is crucial in the development of the arc length formula and in understanding how the sum of these small segments leads to the integral.
πŸ’‘Delta X and Delta Y
Delta X and Delta Y are used in the video to denote small changes in the x and y coordinates, respectively, as one moves along the curve. These terms are essential in constructing the right triangles that approximate the curve's segments. The speaker explains that as Delta X approaches zero, Delta Y becomes the derivative of y with respect to x (dy/dx), which is a key step in deriving the arc length formula.
πŸ’‘Square Root
The square root function is used in the video to calculate the length of the hypotenuse of the right triangles formed by the curve's segments. Specifically, the length of each small segment (delta p) is the square root of the sum of the squares of Delta X and Delta Y. This is a fundamental step in the process of calculating arc length, as it relates to the Pythagorean theorem.
πŸ’‘Integral
An integral in calculus is a way to find the area under a curve, which is analogous to summing an infinite number of infinitesimally small rectangles. In the video, the speaker transitions from summing finite segments (delta p) to an integral as the number of segments approaches infinity and the size of each segment approaches zero. This is a key concept in the derivation of the arc length formula.
πŸ’‘Derivative
The derivative of a function is a measure of its rate of change and is crucial in calculus for understanding how functions behave. In the context of the video, the derivative (dy/dx) is used to describe the slope of the tangent line to the curve at any point, which is essential in calculating the arc length as the curve becomes infinitely small.
πŸ’‘1 + (dy/dx)^2
This expression is central to the arc length formula. The speaker explains that the arc length of a curve can be found by integrating the square root of 1 plus the square of the derivative of y with respect to x. This formula arises from the Pythagorean theorem applied to the right triangles formed by the curve's segments and is a key result in the video's explanation.
πŸ’‘Anti-Derivative
An anti-derivative, or indefinite integral, is the reverse process of differentiation. In the video, the speaker mentions that solving the integral for arc length often involves finding an anti-derivative, which can sometimes be challenging. This concept is crucial in applying the arc length formula to specific functions.
Highlights

Arc length is the first of the real calculus topics studied in a calculus BC course.

Arc length is not included in the calculus AP course.

A curve needs to be rectifiable to find its arc length, which implies it needs to be reasonably smooth.

Curves like sine of one over x are not rectifiable due to their wiggly nature near the origin.

Most curves encountered in the class will be rectifiable and thus have a definable arc length.

The concept of Riemann sum is used to calculate arc length by summing small pieces of the curve.

A small piece of arc length is represented as delta p, with delta x and delta y being its dimensions.

As delta x approaches one, delta y becomes dy/dx.

The length of a small piece of arc is the square root of delta x squared plus delta y squared.

The total arc length is the sum of all these small delta ps.

To find the arc length, multiply by a clever form of one, specifically delta x over delta x.

The bottom delta x can be represented as the square root of delta x squared to simplify the expression.

The expression can be transformed into an integral as delta x gets very small.

The arc length formula is derived as the integral of the square root of one plus (dy/dx) squared dx.

The formula involves taking the derivative of a function, squaring it, adding one, and then finding an anti-derivative.

In most cases, the arc length calculation is either a calculator question or a setup without evaluation.

The video may include a separate session on arc length examples to further illustrate the concept.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 8.13

Lesson 8 - Arc Length (Calculus 2 Tutor)

Lec 31 | MIT 18.01 Single Variable Calculus, Fall 2007

Arc Length of y=x^(3/2) | MIT 18.01SC Single Variable Calculus, Fall 2010

2011 Calculus BC free response #1d | AP Calculus BC | Khan Academy

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Arc LengthCalculus BCRiemann SumDerivativeIntegralMathematicsEducationalTrigonometrySine FunctionRectifiable Curves