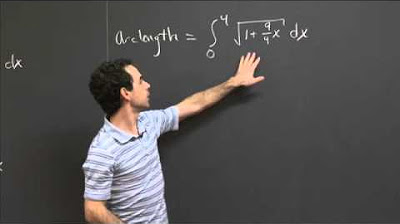AP Calculus BC Lesson 8.13

Elizabeth Fein

26 Nov 202225:04

EducationalLearning

32 Likes 10 Comments

TLDRThis video lesson delves into the concept of arc length, a fundamental aspect of calculus. It explains how to approximate and calculate the length of a smooth curve using integral calculus. The video provides a step-by-step approach, starting with a basic estimation using straight-line distances and progressing towards a more accurate method involving multiple segments. It then introduces the arc length formula, L = ∫(√(1 + (f'(x))^2))dx, from point A to B, and demonstrates its application through several examples. The lesson also touches on related calculus concepts such as the limit definition of the derivative and Riemann sums, emphasizing the importance of limits in calculus. The video concludes with an exploration of the arc length formula's derivation, offering insights into the mathematical processes behind it.

Takeaways

📐 The concept of Arc Length refers to the length of a smooth curve, which can be approximated by dividing the curve into multiple segments and summing the lengths of these segments.
🔍 Accurate Arc Length approximation is achieved by increasing the number of segments used, which is analogous to the limit definition of the derivative and the Riemann sum.
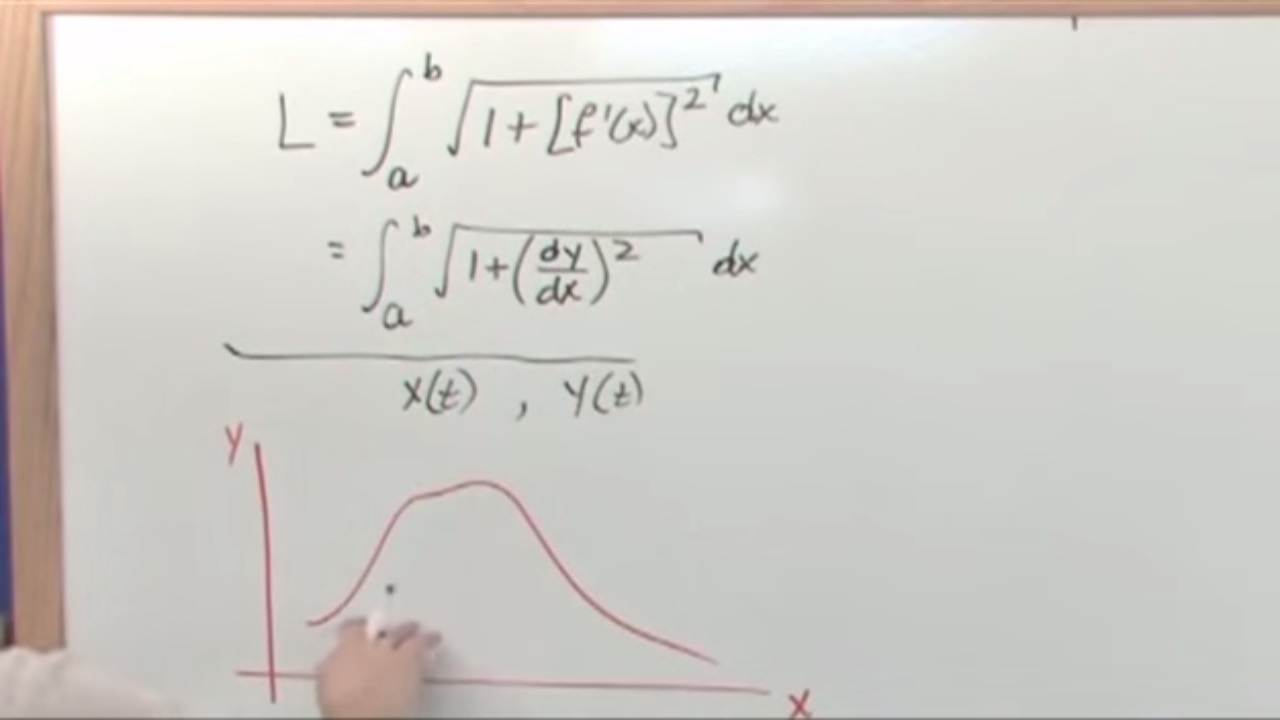
📈 The formula for calculating Arc Length is given by: L = ∫(A to B) √(1 + (F'(x))^2) dx, where F'(x) represents the derivative of the function F(x) with respect to x.
🌐 The Arc Length formula is derived by combining the distance formula with the concept of integration and limits, and it is not required to be memorized for the AP exam.
📊 To find the Arc Length of a function like f(x) = 4cos(x) from x=1 to x=5, one must first find the derivative f'(x) and then apply the Arc Length formula.
🔄 For a function expressed in terms of y (e.g., y = -3y^3), the Arc Length formula can be adapted by changing the variable of integration from x to y.
🧩 When dealing with a curve defined by an integral expression, such as the length of a curve from x=0 to x=8, one must determine the original function by integrating the derivative squared term.
🏞️ The perimeter of a region bounded by curves can be found by summing the straight line distances and the arc lengths of the curvy parts.
📝 When calculating the volume of a solid formed by rotating a region around an axis, the volume is given by V = ∫(A to B) (π/8) * (f(x) - g(x))^2 dx, where f(x) and g(x) are the functions defining the top and bottom curves, respectively.
🤔 The proof of the Arc Length formula is not shown in detail but is based on the limit process and the mean value theorem, which relates the instantaneous rate of change (derivative) to the average rate of change over an interval.

Q & A

What is the concept of Arc Length discussed in the video?
-Arc Length refers to the length of a smooth curve. It is found by approximating the curve with multiple small straight lines and summing their lengths, with the approximation becoming more accurate as the number of segments increases.
How does the video demonstrate the process of finding the Arc Length?
-The video demonstrates the process by dividing the curve into multiple segments and using the straight-line distance between two points as an approximation. It shows that increasing the number of segments leads to a more accurate approximation of the actual curve length.
What is the formula for calculating Arc Length?
-The formula for Arc Length is given by L = ∫ from A to B of the square root of (1 + (F'(x))^2) dx, where F'(x) is the derivative of the function that describes the curve.
How is the Arc Length formula derived?
-The Arc Length formula is derived by combining the distance formula with the concept of integration and limits, and it is similar to the limit definition of the derivative and the limit definition of a Riemann sum.
What is the significance of the limit concept in calculus as explained in the video?
-The limit concept is fundamental in calculus as it is used to define other calculus concepts, including the derivative and the Riemann sum. It helps in approximating values and lengths more accurately as the number of segments or the interval size approaches infinity.
How does the video relate the Arc Length formula to the distance formula?
-The video relates the Arc Length formula to the distance formula by showing that the square root of (1 + (F'(x))^2) is analogous to the square root of (Δx^2 + Δy^2) in the distance formula, with Δy/Δx representing the derivative of the function at a point.
What is the sample multiple-choice question presented in the video?
-The sample multiple-choice question is: What is the length of the curve f(x) = 4cos(x) from x = 1 to x = 5? The solution involves finding the derivative, setting up the Arc Length formula, and evaluating the integral to get the length.
How does the video explain the transition from using x to y in the Arc Length formula?
-The video explains that the transition from x to y in the Arc Length formula involves changing the integration variable from x to y and adjusting the formula to integrate with respect to y, while keeping the same principle of finding the square root of (1 + (F'(y))^2) dy.
What is the importance of the mean value theorem in deriving the Arc Length formula?
-The mean value theorem is important in deriving the Arc Length formula because it guarantees that there exists a value (F'(c_i)) that is equal to the average rate of change over an interval, which allows us to replace the average rate of change with the instantaneous rate of change (the derivative) in the formula.
How does the video illustrate the process of finding the length of a curve using the Arc Length formula?
-The video illustrates this by providing examples where the function of the curve is given, and the task is to find its length over a specified interval. It involves finding the derivative of the function, setting up the integral with the square root of (1 + (derivative)^2), and evaluating the integral to find the length.
What is the practical application of the Arc Length formula shown in the video?
-The practical application shown in the video is finding the perimeter of a region bounded by curves and直线, where the Arc Length formula is used to calculate the lengths of the curvy parts of the boundary.

Outlines

00:00

📐 Introduction to Arc Length

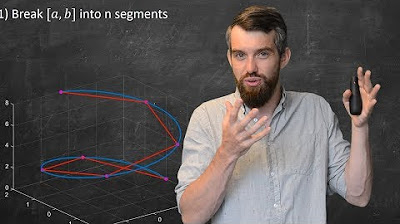
This paragraph introduces the concept of arc length, which is the length of a smooth curve. It explains the process of approximating the arc length by dividing the curve into multiple segments and using the straight-line distance between points as an estimate. The more segments used, the closer the approximation is to the actual curve length. The paragraph also connects this concept to the limit definition of the derivative and the Riemann sum from previous lessons, emphasizing the fundamental role of limits in calculus. The arc length formula is introduced but not proved in detail, with a promise to cover it later in the video.

05:01

📊 Calculating Arc Length with Specific Examples

This section provides a step-by-step guide on how to calculate the arc length using specific examples. It explains the process of finding the derivative of the function, squaring it, and then integrating from the given interval to find the length of the curve. The paragraph includes multiple-choice questions as examples, demonstrating how to apply the arc length formula to different functions, such as cosine and cubic functions. It also highlights the importance of using the correct formula and being cautious of potential pitfalls in multiple-choice questions.

10:02

🌀 Arc Length Formula for Natural Logarithm Function

This paragraph focuses on calculating the arc length of a curve defined by the function y equals 4 times the natural log of x, from x equals 2 to x equals 6. It explains how to find the derivative of the natural log function and how to incorporate it into the arc length formula. The paragraph also addresses common mistakes that could arise from misinterpreting the formula and emphasizes the need for precision in applying the correct mathematical expressions.

15:02

🏞️ Perimeter Calculation for a Region

This paragraph discusses the calculation of the perimeter of a region bounded by specific functions and lines. It explains how to find the intersection points of the functions to determine the straight-line distances and then use the arc length formula to find the length of the curvy part of the boundary. The paragraph provides a detailed explanation of setting up the integral for the arc length and how to combine it with the straight-line distances to find the total perimeter of the region.

20:03

📈 Derivation of the Arc Length Formula

This paragraph delves into the derivation of the arc length formula, providing a detailed explanation of the process. It starts with the basic concept of dividing the curve into small segments and using the distance formula to find the length of each segment. The paragraph then introduces the idea of limits and the mean value theorem to show how the arc length formula is derived from the sum of these segment lengths as the number of segments approaches infinity. The explanation includes the use of calculus concepts such as derivatives and integrals, and it emphasizes the connection between this formula and other fundamental calculus concepts.

Mindmap

Keywords

💡Arc Length

Arc Length refers to the distance along the curve of a function between two points. It is the main concept discussed in the video, where the speaker explains how to calculate it using integral calculus. The video provides examples of finding the arc length of different curves, such as from x=0 to x=6, and illustrates how increasing the number of segments used in approximation improves the accuracy of the calculation.

💡Integral

In the context of the video, an integral is a fundamental concept in calculus used to calculate the area under a curve, which is essential in finding the arc length. The speaker explains that the arc length formula involves integrating the square root of 1 plus the derivative of the function squared from point A to point B.

💡Derivative

The derivative of a function represents the rate of change or the slope of the function at a given point. In the video, the derivative is crucial for calculating the arc length, as it appears in the integrand of the arc length formula.

💡Approximation

Approximation in this video refers to the process of estimating the arc length by dividing the curve into smaller segments and using the straight-line distances between these segments. The more segments used, the closer the approximation is to the actual arc length.

💡Limit

The limit is a fundamental concept in calculus that describes the value a function approaches as the input (or another variable) approaches a certain point. In the context of arc length, the video mentions the limit definition of the derivative and the Riemann sum, which are used to derive the arc length formula.

💡Riemann Sum

A Riemann Sum is a method used to approximate the definite integral of a function by dividing the interval into smaller subintervals and summing the areas of rectangles or other shapes that approximate the curve. The video connects the concept of Riemann Sums to the process of approximating arc length.

💡Curve

A curve in mathematics is a continuous set of points, each defined by a pair of coordinates (x, y), that form a smooth shape. In the video, the focus is on finding the arc length of various curves defined by different mathematical functions.

💡Function

A function in mathematics is a relation that assigns a single output value to each input value. Functions are central to the video, as the arc lengths are calculated for specific functions, and their derivatives are used in the arc length formula.

💡Square Root

The square root of a number is a value that, when multiplied by itself, gives the original number. In the video, the square root is used in the arc length formula to calculate the length of the curve by taking the square root of 1 plus the derivative of the function squared.

💡Calculus

Calculus is a branch of mathematics that deals with rates of change and accumulation. The video's content is rooted in calculus, particularly in the areas of integration and derivatives, which are used to find arc lengths.

💡Mean Value Theorem

The Mean Value Theorem in calculus states that for a continuous and differentiable function on a closed interval, there exists at least one point in the open interval where the derivative equals the average rate of change over that interval. The video briefly mentions this theorem in the context of deriving the arc length formula.

Highlights

Introduction to Arc Length and its importance in calculus.

Arc Length as the length of a smooth curve, contrasted with straight-line distance.

Method of dividing the curve into segments to approximate Arc Length more accurately.

Connection between Arc Length approximation and the Limit definition of the derivative.

Arc Length formula derivation combining distance formula and integration.

Example of calculating Arc Length for f(x) = 4cos(x) from x=1 to x=5.

Transition of Arc Length formula from x to y coordinates.

Calculation of Arc Length for f(y) = -3y^3 from y=-1 to y=2.

Arc Length calculation for y = 4ln(x) from x=2 to x=6 with a focus on avoiding common mistakes.

Determination of a curve's equation given its Arc Length integral and a point on the curve.

Use of Arc Lengths to find the perimeter of a region bounded by curves and lines.

Graphing functions to find the intersection points for calculating region perimeter.

Integration of top curve minus bottom curve to find the area of a region.

Volume calculation of a solid with semicircular cross-sections using integrals.

Explanation of the Arc Length formula derivation using limits and mean value theorem.

Comparison of the process for finding Arc Length to the Riemann sum and derivative limit definitions.

Final summary emphasizing the complexity of the Arc Length formula derivation and its non-necessity for the AP exam.

Transcripts

Browse More Related Video

Arclength

Arc Length of y=x^(3/2) | MIT 18.01SC Single Variable Calculus, Fall 2010

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

Lesson 8 - Arc Length (Calculus 2 Tutor)

Find the Arc Length of a Function with Calculus

How long is a curve?? The Arclength Formula in 3D

Related Tags

Arc Length Calculus Concepts Derivative Definition Riemann Sum Integral Application Mathematical Analysis Curve Approximation AP Exam Prep Educational Content Math Tutorial