Wave Equation
TLDRIn this AP Physics essentials video, Mr. Andersen explores the wave equation by demonstrating wave generation on a string. He explains the role of amplitude (A) and wavelength (lambda) in forming a cosine wave, which is the basis for the wave equation. The video delves into both position-based (f(x)) and time-based (f(t)) wave equations, highlighting the relationship between period, frequency, and wave properties. Interactive simulations using GeoGebra and a gear model help visualize the concepts, allowing viewers to manipulate amplitude and wavelength to observe the effects on wave patterns, providing a clear understanding of how these elements construct the wave equation.
Takeaways
- 🌊 The video is about the wave equation, explaining how waves are generated and how they can be mathematically described.
- 📚 Mr. Andersen uses a string to demonstrate that energy is transferred through the string without the string itself moving.
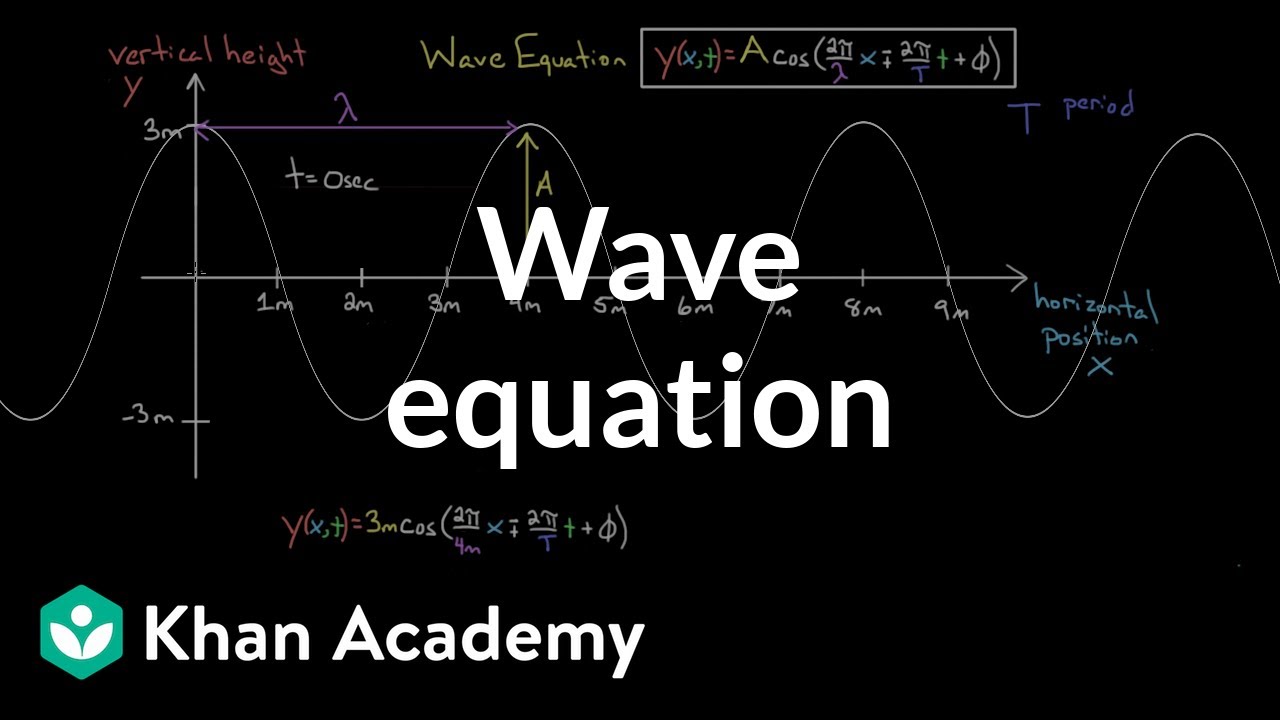
- 📏 The wave equation is given by f(x) = A * cos(2π / λ * x), where A is the amplitude, λ is the wavelength, and x is the position.
- 🔄 Transverse waves can be described using a cosine or sine wave function, which relates to the position and amplitude of the wave.
- ⏱ The wave equation can also be a function of time, f(t) = A * cos(2π / T * t), where T is the period of the wave.
- 🔁 The period T is the time between oscillations, and the frequency is the reciprocal of the period (frequency = 1/T).
- 🔧 A PHET simulation is introduced to visually demonstrate how a wave is generated by the rotation of a gear.
- 📈 The GeoGebra simulation allows viewers to manipulate the amplitude (A) and the factor inside the cosine function (B) to see the effects on wave characteristics.
- 📊 Increasing A results in a larger wave, indicating a greater amplitude, while decreasing A results in a smaller wave.
- 🔍 Adjusting B affects the wavelength; increasing B decreases the wavelength, and decreasing B increases the wavelength.
- 📐 The relationship between the value inside the cosine function (2π / λ or 2π / T) and the wavelength or period is inversely proportional, affecting how waves are compressed or stretched.
Q & A
What is the main topic of the video?
-The main topic of the video is the wave equation, focusing on how it relates to the amplitude and wavelength of a wave.
What is the wave equation described in the video?
-The wave equation described in the video is f(x) = A * cosine(2 * pi / lambda), where A is the amplitude, lambda is the wavelength, and x is the position.
How does the amplitude (A) affect the wave in the equation?
-The amplitude (A) determines the height of the wave. As A increases, the wave becomes larger, and as A decreases, the wave becomes smaller.
What is the significance of lambda (λ) in the wave equation?
-Lambda (λ) represents the wavelength of the wave. It affects the spacing between the peaks of the wave, with a larger lambda resulting in a longer wavelength and a smaller lambda resulting in a shorter wavelength.
What is the relationship between wavelength and period in the context of waves?
-The period is the time it takes for one complete wave cycle to occur. The relationship between wavelength and period is such that the period is the distance in time between oscillations, and frequency is the reciprocal of the period.
How can the wave equation be represented in terms of time?
-The wave equation can be represented in terms of time as f(t) = A * cosine(2 * pi / T), where T is the period of the wave.
What is a transverse wave?
-A transverse wave is a type of wave where the displacement of the medium is perpendicular to the direction of the wave's propagation, like the waves on a string.
What is the purpose of the PHET simulation mentioned in the video?
-The PHET simulation is used to visually demonstrate the generation of a wave as a gear rotates, helping to understand the principles behind the wave equation.
What is the role of a unit circle in generating a wave?
-A unit circle, when moved over time, can generate a wave pattern. It is a mathematical tool used to visualize and understand wave formation.
What is GeoGebra, and how is it used in the video?
-GeoGebra is a dynamic mathematics software that allows for interactive simulations. In the video, it is used to explore and manipulate the wave equation to see the effects of changing amplitude and wavelength.
How does changing the value of B in the equation f(x) = cosine(Bx) affect the wave?
-Changing the value of B affects the frequency of the wave. As B increases, the frequency increases, leading to a shorter wavelength, and as B decreases, the frequency decreases, leading to a longer wavelength.
What does the video suggest about the relationship between frequency and period?
-The video suggests that frequency is the reciprocal of the period, meaning that as the period increases, the frequency decreases, and vice versa.
Outlines
🌀 Introduction to the Wave Equation
In this introductory segment, Mr. Andersen presents the concept of the wave equation in the context of AP Physics. He demonstrates the generation of waves on a string, emphasizing that the string itself doesn't move but rather serves as a medium for energy transfer. He introduces the cosine wave as a representation of the wave pattern created. The amplitude (A) and wavelength (lambda) are identified as key components of the wave equation, which can be expressed in terms of position (x) as f(x) = A * cos(2π/λ * x). The video also touches on the use of sine waves for describing transverse waves and the significance of amplitude and wavelength in shaping the wave's characteristics.
🕒 Wave Equation as a Function of Time
This part of the video script delves into the temporal aspect of wave equations. Mr. Andersen explains how the wave equation can be expressed in terms of time (t) instead of position, with the equation f(t) = A * cos(2π/T * t), where T represents the period of the wave. He clarifies the relationship between period and frequency, stating that frequency is the reciprocal of the period (frequency = 1/T). This section also introduces the concept of using frequency in wave equations, offering an alternative perspective on wave analysis.
🔧 Interactive Simulations to Explore Wave Properties
The script transitions into the use of interactive simulations to explore and understand wave properties. Mr. Andersen uses a gear mechanism to visually demonstrate wave generation and the resulting wave pattern. He then introduces a unit circle concept to explain how a wave can be generated over time. The GeoGebra simulation is highlighted as a tool for adjusting the amplitude (A) and the parameter inside the cosine function (B), which affects the wavelength. The simulation allows viewers to see how changes in A and B impact the wave's amplitude and wavelength, respectively.
📉 Analyzing the Wave Equation's Parameters
In this segment, Mr. Andersen focuses on the mathematical aspects of the wave equation. He uses the GeoGebra simulation to illustrate the effects of varying the amplitude (A) and the term inside the parentheses (B), which is related to the wavelength. By adjusting A, viewers can observe how the wave's amplitude increases or decreases. Similarly, altering B affects the wavelength, with an increase in B leading to a shorter wavelength and a decrease resulting in a longer one. The script provides a clear mathematical explanation of how these parameters influence the wave's properties.
🔄 Understanding Wave Equations in Terms of Position and Time
The final part of the script revisits the wave equation, this time emphasizing its application in terms of both position and time. Mr. Andersen explains how the same wave equation can be used to describe waves by adjusting the parameters to represent either position (x) or time (t). He demonstrates how increasing the period (T) affects the wave's period and how frequency is inversely related to it. The script concludes with an encouragement for viewers to grasp the concepts of constructing wave equations based on wavelength and amplitude or period and amplitude, depending on the axis labeling.
Mindmap
Keywords
💡Wave Equation
💡Amplitude (A)
💡Wavelength (λ, lambda)
💡Transverse Waves
💡Cosine Wave
💡Period (T)
💡Frequency
💡Position (x)
💡Time (t)
💡Simulation
💡Unit Circle
Highlights
Introduction to the wave equation in AP Physics essentials video 106.
Demonstration of wave generation in a string without string movement, only energy transfer.
Explanation of the cosine wave as a representation of the wave created.
Definition of amplitude (A) and wavelength (lambda) in the context of the wave equation.
Wave equation formulation containing amplitude and wavelength affecting wave position.
Use of cosine or sine waves to describe transverse waves.
Introduction of the wave equation as a function of position (f(x)).
Inclusion of amplitude and wavelength in the wave equation for position.
Transition to the wave equation as a function of time (f(t)).
Inclusion of amplitude and period in the time-based wave equation.
Explanation of frequency as the reciprocal of period.
Occurrence of frequency in the wave equation instead of period.
Introduction to a PHET simulation to visualize wave generation.
Use of a unit circle and its movement over time to generate and visualize waves.
GeoGebra simulation to explore the effects of amplitude (A) on wave characteristics.
GeoGebra simulation to explore the effects of wavelength (B) on wave characteristics.
Application of amplitude and wavelength changes to the wave equation.
Explanation of how wavelength affects the value inside the wave equation's parenthesis.
Transition from position-based to time-based wave equation visualization.
Impact of period changes on the wave equation and wave characteristics.
Inclusion of frequency in the wave equation and its effect on wave visualization.
Summary of constructing equations relating wavelength, amplitude, period, and frequency of waves.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: