Inverse Functions - Domain & range- With Fractions, Square Roots, & Graphs
TLDRThis video tutorial offers a comprehensive guide on finding inverse functions algebraically and graphically. It begins with linear functions, illustrating the process of swapping x and y to derive the inverse, and progresses to more complex rational and radical functions. The video explains how to solve for the inverse algebraically, discusses the importance of domain and range in relation to inverse functions, and demonstrates how to graph inverse functions using symmetry across the line y=x. It also covers how to prove two functions are inverses by composing them and shows the application of the vertical and horizontal line tests to determine if a function has an inverse.
Takeaways
- 🔄 The inverse function is found by switching the x and y values of the original function.
- 📚 To find the inverse of a function like f(x) = 3x - 8, replace f(x) with y, switch x and y, and solve for y, resulting in the inverse function y = (x + 8) / 3.
- 📈 When graphing inverse functions, the symmetry across the line y = x is evident, indicating the relationship between the original function and its inverse.
- 📝 For rational functions, like f(x) = (2x + 5) / (3x - 1), finding the inverse involves cross-multiplication, distributing, and isolating y to get the inverse function.
- 🛑 The domain and range of the original function become the range and domain of the inverse function, respectively.
- 📉 For square root functions, the domain starts from the value inside the square root and goes to infinity, while the range is from zero to infinity.
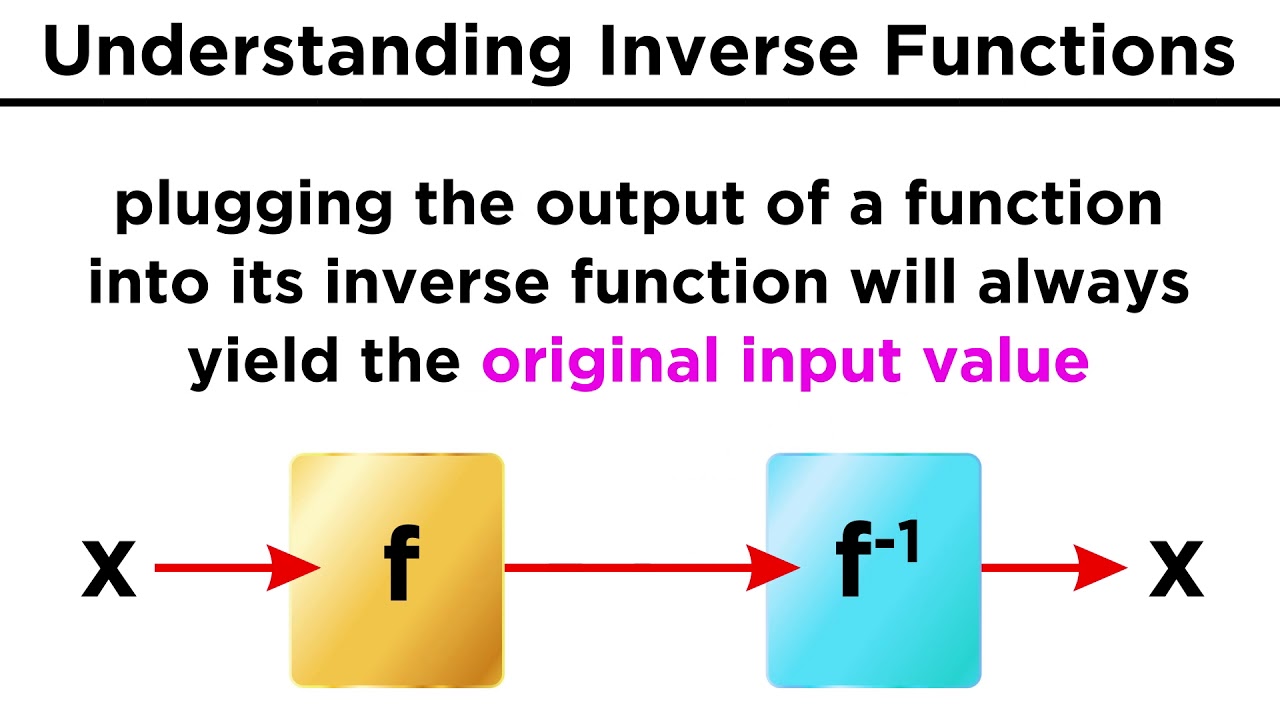
- 📌 To prove two functions are inverses, compute the composite functions f(g(x)) and g(f(x)), which should both equal x if the functions are indeed inverses.
- 📐 The vertical line test determines if a curve is a function, while the horizontal line test checks if a function has an inverse.
- 📊 A function that passes the horizontal line test is one-to-one and therefore has an inverse, which will pass the vertical line test.
- 📈 The graph of an inverse function can be determined by switching the coordinates of points on the original function's graph.
- 📘 For exponential and logarithmic functions, the inverse is found by using the natural logarithm to bring down the exponent and then isolating y.
Q & A
What is an inverse function in algebraic terms?
-An inverse function is a function where the roles of the input (x) and output (y) values are switched. If f(x) = y, then the inverse function f^(-1)(y) = x.
How do you find the inverse of a linear function such as f(x) = 3x - 8?
-To find the inverse of f(x) = 3x - 8, replace f(x) with y, switch x and y, and solve for y. This results in the inverse function y = (x + 8) / 3.
What is the process for finding the inverse of a rational function?
-To find the inverse of a rational function, replace f(x) with y, switch x and y, and solve for y. This involves cross-multiplying, isolating y, and simplifying the equation.
Can you provide an example of finding the inverse of a square root function?
-For a square root function like f(x) = √(2x - 6), replace y with f(x), switch x and y, square both sides to eliminate the square root, and solve for y to get the inverse function y = √(x^2 + 6) / 2 - 3.
What is the domain and range of the original square root function f(x) = √(2x - 6)?
-The domain of the original function is [3, ∞) since the expression inside the square root must be non-negative. The range is [0, ∞) as the square root function cannot yield negative values.
How do you determine the domain and range of the inverse function?
-The domain and range of the inverse function are switched compared to the original function. If the original function's range is [a, b], the inverse function's domain will be [a, b], and vice versa for the range.
What is the significance of the vertical line test in determining if a graph represents a function?
-The vertical line test checks if any vertical line intersects the graph at more than one point. If it does, the graph does not represent a function because a function must pass the horizontal line test, having only one y-value for each x-value.
How can you prove that two functions are inverses of each other?
-To prove two functions are inverses, you need to show that the composite function f(g(x)) equals x and that g(f(x)) also equals x, demonstrating that applying one function and then the other returns the original input.
What is the process for graphing the inverse function based on given points of the original function?
-To graph the inverse function, switch the x and y coordinates of the given points of the original function and plot them. The resulting graph will be symmetrical across the line y = x.
Why does the inverse of an exponential function like f(x) = e^(3x + 1) - 5 involve taking the natural log of both sides?
-The inverse of an exponential function requires isolating the exponent, which is achieved by taking the natural log of both sides. This operation brings the exponent down to the front, allowing you to solve for y in the inverse function.
How do you find the inverse function of a cube root function like f(x) = cube root of (x - 4 + 1)?
-For a cube root function, replace f(x) with y, switch x and y, and raise both sides to the third power to eliminate the cube root. Then solve for y to find the inverse function.
Outlines
📚 Finding and Graphing Inverse Functions
This paragraph introduces the concept of inverse functions, explaining how to algebraically find the inverse of a given function by swapping the x and y variables and solving for y. The process is demonstrated using the linear function f(x) = 3x - 8, resulting in the inverse function x + 8 / 3. The paragraph also invites viewers to find the inverse of a rational function and discusses the importance of understanding the switch between x and y to reverse the original function.
🔍 Inverse Functions of Square Root and Cube Root Functions
The second paragraph delves into finding the inverse functions of more complex expressions, such as square root and cube root functions. It explains the algebraic steps to isolate y and find the inverse, including squaring both sides to eliminate the square root and raising both sides to the third power for the cube root. The domain and range of the original and inverse functions are also discussed, emphasizing the switch between them when finding the inverse.
📈 Graphing Inverse Functions and Proving Inverse Relationships
This paragraph focuses on graphing inverse functions using given points and the symmetry across the line y = x. It also explains how to prove two functions are inverses of each other by composing them and showing that the result is the identity function, x. The process involves substituting one function into the other and simplifying to demonstrate the inverse relationship.
📉 Understanding Vertical and Horizontal Line Tests for Functions and Their Inverses
The fourth paragraph discusses the use of the vertical line test to determine if a curve is a function and the horizontal line test to check if a function has an inverse. It explains that a function must pass the vertical line test to have an inverse, which in turn must pass the horizontal line test. The paragraph uses examples to illustrate the tests and the concept of one-to-one functions, which are essential for having an inverse.
📊 The Importance of One-to-One Functions for Inverses
The final paragraph reinforces the importance of one-to-one functions for the existence of inverses. It uses the horizontal line test to show that a function with a single intersection point per horizontal line has an inverse. Conversely, if a function does not pass the horizontal line test, indicating multiple y-values for a single x-value, its inverse will not be a function, as it will not pass the vertical line test. The paragraph concludes with the significance of the one-to-one nature of functions for their invertibility.
Mindmap
Keywords
💡Inverse Function
💡Algebraic Manipulation
💡Domain and Range
💡Rational Function
💡Square Root Function
💡Cube Root Function
💡Exponential Function
💡Natural Logarithm
💡Vertical Line Test
💡Horizontal Line Test
Highlights
Introduction to finding the inverse function algebraically and graphing inverse functions.
Explanation of the concept of an inverse function where X and Y values are switched.
Step-by-step method to find the inverse of a linear function, such as 3x - 8.
Demonstration of solving for the inverse function by adding and dividing to isolate Y.
Use of inverse notation to represent the inverse function of a linear function.
Approach to finding the inverse of a rational function, exemplified by 2x + 5 / (3x - 1).
Technique of cross-multiplication and distribution to solve for the inverse of a rational function.
Isolation of Y by factoring and dividing both sides by the common factor to find the inverse function.
Process of finding the inverse of a square root function and determining its domain and range.
Explanation of squaring both sides to eliminate the square root when finding an inverse function.
Switching the domain and range of the original function to find those of the inverse function.
Graphical representation of the square root function and its inverse, showing symmetry across y=x.
Finding the inverse function of a cube root function and its unrestricted domain and range.
Difference between even and odd index radicals in terms of domain and range restrictions.
Method to find the inverse function of an exponential function using natural logarithms.
Graphing the inverse function using given points and symmetry with respect to the line y=x.
Process to prove two functions are inverses of each other by using composite functions.
Use of the vertical line test to determine if a graph represents a function.
Application of the horizontal line test to ascertain the existence of an inverse function.
Importance of the one-to-one property of functions for the existence of an inverse function.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: