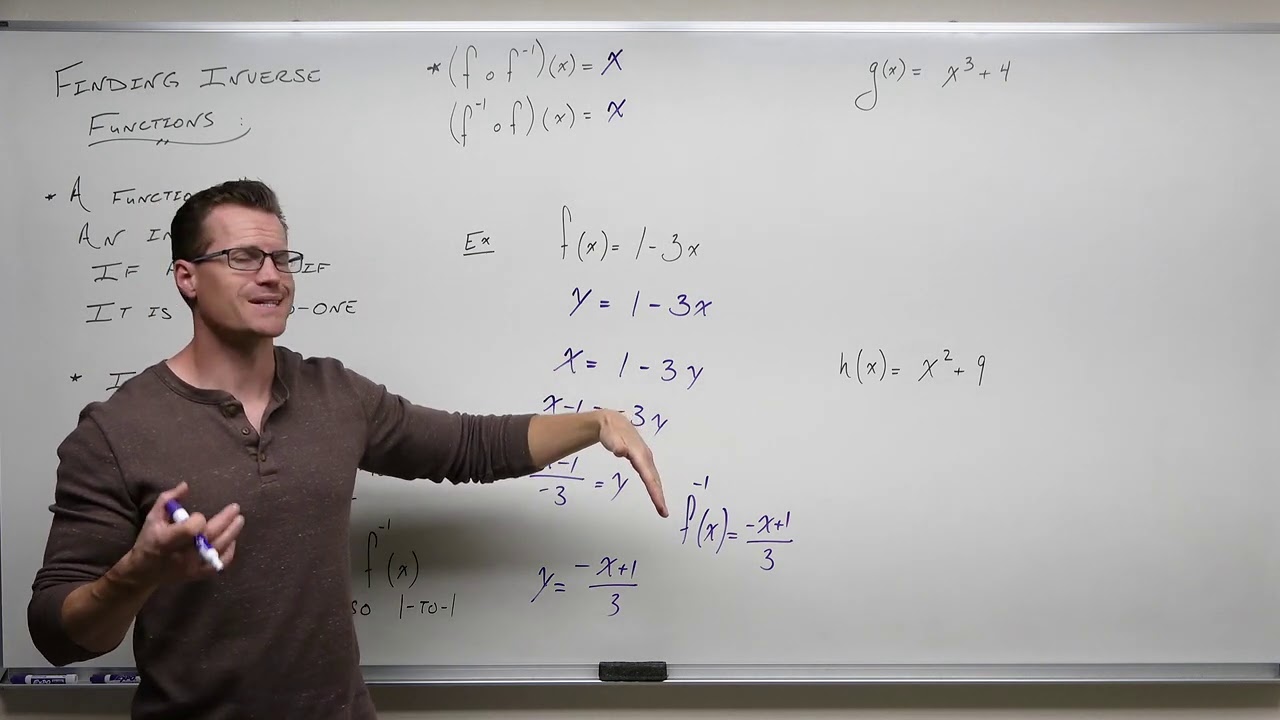12 - What are Inverse Functions? (Part 1) - Find the Inverse of a Function & Graph
TLDRThis lesson delves into the concept of inverse functions, a topic that often perplexes students. The instructor aims to clarify what an inverse function is and its significance in mathematics. Starting with the basics of solving equations by 'undoing' operations on 'x', the lesson progresses to explain additive and multiplicative inverses. It then extends these ideas to functions, illustrating how to identify and work with inverse functions, including the graphical representation of inverse functions as reflections over the line y=x. The importance of the horizontal line test for a function to have an inverse is also discussed, with examples provided to cement understanding.
Takeaways
- 🧠 Inverse functions are a concept that can be challenging for students, but they are crucial for solving more complex equations in mathematics.
- 🔄 The idea of inverses extends beyond basic arithmetic to functions, where an inverse function 'undoes' the action of the original function.
- 📚 To solve equations for x, one must perform inverse operations to isolate x, such as subtracting instead of adding, or dividing instead of multiplying.
- ➕ The additive inverse is used to 'undo' addition, and it is represented by the number with the opposite sign.
- 🔄 The multiplicative inverse 'undoes' multiplication, exemplified by multiplying by a fraction to return to the original number.
- 🤔 Understanding inverses is essential for grasping more advanced mathematical concepts, such as logarithms, which are the inverses of exponential functions.
- 📉 The process of finding an inverse function involves applying the inverse operation to both the function and its output to return to the original input.
- 📚 The script provides a step-by-step explanation of how to determine if two functions are inverses of each other through the use of composite functions.
- 📈 The graphical representation of inverse functions is achieved by reflecting the graph of the original function over the line y=x, resulting in a mirror image.
- 📊 For a function to have an inverse, it must pass the horizontal line test, meaning each horizontal line intersects the function at most once.
- 🚫 Not all functions have inverses, such as the quadratic function f(x) = x^2 over its entire domain, because it fails the horizontal line test.
Q & A
What is the main topic of this lesson?
-The main topic of this lesson is inverse functions, focusing on understanding what an inverse function is, its importance in mathematics, and how to identify and work with them.
Why are inverse functions important in mathematics?
-Inverse functions are important because they allow us to 'undo' operations in more complex equations, particularly useful when solving for variables in exponential and logarithmic equations.
What is the relationship between an additive inverse and a multiplicative inverse?
-The additive inverse is used to 'undo' addition by subtracting the same number, while the multiplicative inverse 'undoes' multiplication by using division or the reciprocal of the original number.
Can you explain the concept of a function having an inverse?
-A function has an inverse if every output from the original function corresponds to a unique input, and applying the inverse function to that output returns the original input, essentially 'undoing' the original function.
What is the graphical representation of an inverse function?
-Graphically, an inverse function is a reflection of the original function over the line y = x, creating a mirror image where the coordinates of each point are flipped.
How do you determine if a function has an inverse?
-A function has an inverse if it passes the horizontal line test, meaning that for any given y-value, there is only one corresponding x-value.
What is the significance of the horizontal line test in determining if a function has an inverse?
-The horizontal line test checks if a function is one-to-one, which is necessary for a function to have an inverse. If a horizontal line intersects the graph at more than one point, the function does not have an inverse over that domain.
Can all functions have inverses?
-No, not all functions have inverses. For a function to have an inverse, it must be one-to-one and pass the horizontal line test.
What is an example of a function that does not have an inverse?
-An example of a function that does not have an inverse is the quadratic function f(x) = x^2, as it fails the horizontal line test and therefore cannot be inverted over its entire domain.
How are inverse functions used in solving exponential equations?
-Inverse functions, such as the logarithm for the exponential function, are used to 'undo' the exponentiation, allowing the variable to be isolated and solved for.
Outlines
📚 Introduction to Inverse Functions
The video script begins with an introduction to the concept of inverse functions, which are often challenging for students. The instructor aims to clarify what an inverse function is, how it is graphically represented, and its significance in mathematics. The lesson starts with a review of solving equations by reversing operations, such as addition and multiplication, using inverses. The idea of additive and multiplicative inverses is explained as a precursor to understanding function inverses. The instructor also introduces the concept of using inverse functions to solve more complex equations, such as those involving exponential functions and their inverses, logarithms.
🔍 Exploring Inverse Functions and Their Applications
This paragraph delves deeper into the concept of inverse functions, using a simple function as an example. The instructor explains how to identify inverse functions and demonstrates this with two specific functions, f(x) and g(x), which are inverses of each other. The concept of 'undoing' mathematical operations is emphasized, showing how applying an inverse function can revert the original function's effect. The lesson illustrates this with examples of composite functions, where the order of application does not affect the outcome due to the properties of inverse functions.
🔄 The Symmetry of Inverse Functions
The script continues to explore the symmetry inherent in inverse functions, emphasizing that applying a function and its inverse will always return the original input, regardless of the order in which they are applied. This is demonstrated with numerical examples and the concept of composite functions. The instructor reinforces the idea that inverse functions are not random but are specifically designed to reverse each other's effects, which is crucial for solving complex equations in higher mathematics.
📉 Visualizing Inverse Functions with Graphs
The instructor shifts the focus to the graphical representation of inverse functions, explaining that the graph of an inverse function is a mirror reflection of the original function across the line y=x. This is illustrated by graphing two linear functions and showing how their inverses are reflections of each other. The concept of the horizontal line test is introduced as a method to determine if a function has an inverse, with the requirement that a function must pass this test to ensure its inverse will pass the vertical line test.
📌 Identifying Points on Inverse Function Graphs
This section of the script discusses how to identify points on the graphs of inverse functions. The instructor demonstrates how each point on the original function corresponds to a 'mirrored' point on the inverse function, with coordinates that are flipped. This visual representation reinforces the concept of inverse functions 'undoing' each other's effects, as the input and output are returned to their original values when passed through both functions in any order.
🚫 Not All Functions Have Inverses
The script concludes with a cautionary note that not all functions possess inverses. The instructor explains the importance of the horizontal line test for determining if a function can have an inverse. Functions that fail this test, such as the quadratic function f(x) = x^2, do not have inverses over their entire domain because they do not pass the vertical line test when reflected over the line y=x. The lesson ends with a preview of future topics, including calculating and sketching inverse functions and further practice with the horizontal line test.
Mindmap
Keywords
💡Inverse Function
💡Additive Inverse
💡Multiplicative Inverse
💡Composite Functions
💡Exponential Function
💡Logarithm
💡Reflection
💡Horizontal Line Test
💡Vertical Line Test
💡Graphing Inverse Functions
Highlights
The lesson introduces the concept of inverse functions, which are essential in mathematics and often challenging for students.
An inverse function is defined as a function that 'undoes' another function, similar to how additive and multiplicative inverses work in basic arithmetic.
The lesson explains that to solve equations, one often applies the inverse operation to isolate the variable, previewing the importance of inverse functions in equation solving.
The concept of additive inverse is reviewed, emphasizing its role in reversing the addition operation.
Multiplicative inverse is discussed, showing how division is the inverse operation of multiplication.
The lesson provides a concrete example of inverse functions, f(x) and g(x), demonstrating that applying one function and then its inverse returns the original input.
The graphical representation of inverse functions is introduced, explaining that they are mirror images of each other across the line y=x.
The lesson illustrates how to determine if two functions are inverses by composing them and showing that the result is the identity function (f(g(x)) = x and g(f(x)) = x).
The importance of inverse functions in solving more complex equations, such as exponential equations, is highlighted, with a mention of logarithms as the inverse of exponentials.
The process of graphing inverse functions is demonstrated, showing that the graph of an inverse function is a reflection of the original function over the line y=x.
The lesson explains the horizontal line test as a method to determine if a function has an inverse, where only functions that pass this test have inverses.
An example is given to show that not all functions, such as the quadratic function f(x) = x^2, have inverses over their entire domain due to failing the horizontal line test.
The lesson concludes by emphasizing the importance of understanding inverse functions for further studies in algebra, precalculus, and calculus.
A summary of the entire lesson is provided, encapsulating the definition, graphical representation, and practical implications of inverse functions.
The lesson previews the next part of the series, where students will learn how to calculate inverse functions and apply the horizontal line test to various functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: