INTRODUCTION TO PARABOLA | GRAPHING | VERTEX AT THE ORIGIN | PROF D
TLDRThis educational video script delves into the concept of conic sections, specifically focusing on the parabola. It defines a parabola as the set of points equidistant from a focus and a directrix. The script covers the standard form equations of parabolas, their orientation based on the value of 'p', and how to sketch them using vertex and endpoints. It also explains terms like 'latus rectum', 'focus', 'axis of symmetry', and 'directrix'. The script concludes with examples illustrating how to determine the parabola's orientation, calculate the focus, lattice rectum endpoints, and directrix equation, providing a comprehensive understanding of parabolas.
Takeaways
- 📚 A parabola is a type of conic section defined as the set of all points equidistant from a focus and a directrix.
- 📐 The parabola's symmetry is with respect to its directrix, a fixed line.
- 📈 The vertex of a parabola is the point where the curve changes direction, moving from left to right.
- 📉 The standard form equations of a parabola with the vertex at the origin are \( y^2 = 4px \) for rightward opening and \( x^2 = 4py \) for upward opening.
- ➡️ If \( p \) is positive, the parabola opens to the right or upward; if \( p \) is negative, it opens to the left or downward.
- 📏 The length of the latus rectum, a segment from the vertex perpendicular to the directrix, is \( 4p \).
- 📍 The endpoints of the latus rectum are \( (p, \pm 2p) \) for a vertical parabola and \( (\pm 2p, p) \) for a horizontal one.
- 🔍 The axis of symmetry for a parabola is a vertical line \( x = h \) if the vertex is at the origin, or a horizontal line \( y = k \) if the vertex is at the origin.
- 🔧 The directrix's equation is \( x = -p \) for a vertical parabola and \( y = -p \) for a horizontal one.
- 📝 To graph a parabola, identify the direction it opens, find the focus, endpoints of the latus rectum, and the equation of the directrix.
- 📚 Examples provided in the script demonstrate how to determine the opening direction, calculate the focus, endpoints of the latus rectum, and the directrix equation for given parabola equations.
Q & A
What is a parabola?
-A parabola is defined as the set of all points such that the distance from a point on the parabola to a focus point is the same as the distance from the same point on the parabola to a fixed line called the directrix.
What are the key parts of a parabola?
-The key parts of a parabola include the focus, directrix, vertex, and the endpoints of the lattice rectum.
What is the vertex of a parabola?
-The vertex is the point where the curve changes direction. It is a significant point used in sketching the parabola.
How does the value of 'p' affect the direction a parabola opens?
-If 'p' is greater than zero, the parabola opens to the right or upward. If 'p' is less than zero, the parabola opens to the left or downward.
What is the standard form equation of a parabola with vertex at the origin?
-The standard form equations are y² = 4px for parabolas opening right or left, and x² = 4py for parabolas opening upward or downward.
How do you find the endpoints of the lattice rectum?
-For y² = 4px, the endpoints are (p, ±2p). For x² = 4py, the endpoints are (±2p, p).
What is the axis of symmetry for a parabola?
-For y² = 4px, the axis of symmetry is the y-axis (x = 0). For x² = 4py, the axis of symmetry is the x-axis (y = 0).
What is the equation of the directrix for a parabola?
-For y² = 4px, the directrix is x = -p. For x² = 4py, the directrix is y = -p.
How do you determine the direction a parabola opens given an equation?
-For an equation in the form y² = 4px, if p > 0, it opens to the right; if p < 0, it opens to the left. For x² = 4py, if p > 0, it opens upward; if p < 0, it opens downward.
What steps are involved in graphing a parabola?
-First, identify the vertex, focus, and directrix. Then plot the vertex and draw the axis of symmetry. Next, determine the direction the parabola opens and plot the endpoints of the lattice rectum. Finally, sketch the parabola using these points.
Outlines
📚 Introduction to Conic Sections and Parabolas
The video script begins with an introduction to conic sections, focusing on the parabola. A parabola is defined as a set of points equidistant from a focus and a directrix. The script explains the concept of symmetry with respect to the directrix and introduces key terms such as vertex and focus. The standard form equations of a parabola are presented, including 'y^2 = 4px' for parabolas opening to the right or left, and 'x^2 = 4py' for those opening upward or downward, depending on the sign and value of 'p'.
📐 Parabola Characteristics and Equations
This paragraph delves deeper into the characteristics of parabolas, discussing the implications of the value of 'p' on the direction in which the parabola opens. It also covers the latus rectum, endpoints, axis of symmetry, and directrix, providing equations for each. The paragraph includes an example to illustrate how to determine the direction of a parabola, find the focus, endpoints of the latus rectum, and the equation of the directrix, concluding with a graph of the equation.
🔍 Analyzing Parabola Equations and Graphs
The script continues with an exploration of parabola equations, emphasizing the standard form and how to manipulate it to understand the parabola's orientation. It provides a step-by-step guide to solving for 'p' and determining the focus, endpoints, axis of symmetry, and directrix from a given equation. The paragraph also includes an example problem that demonstrates these concepts in practice.
📘 Further Examples of Parabola Equations
This section presents additional examples of parabola equations, guiding the viewer through the process of converting them into standard form and solving for 'p'. It explains how to identify the direction in which the parabola opens based on the value of 'p' and provides the equations for the focus, endpoints, axis of symmetry, and directrix for each example.
📚 Concluding the Discussion on Parabolas
The final paragraph wraps up the discussion on parabolas by summarizing the key points covered in the video. It reiterates the importance of understanding the standard form equations, the value of 'p', and how these elements relate to the graphical representation of a parabola. The script also encourages viewers to ask questions or seek clarifications in the comments section.
👋 Closing Remarks and Sign Off
The video concludes with a sign-off from the presenter, Professor D, who thanks the viewers for watching and invites them to engage with the content by asking questions or seeking further clarification. The script ends on a friendly note, with a reminder to catch the next video in the series.
Mindmap
Keywords
💡Conic Section
💡Parabola
💡Focus
💡Directrix
💡Vertex
💡Standard Form
💡Endpoints
💡Axis of Symmetry
💡Lattice Rectangle
💡Parameter p
💡Graph
Highlights
A parabola can be defined as the set of all points such that the distance from a point on the parabola to a focus point is the same as the distance from the same point to a fixed line called the directrix.
The parabola is symmetric with respect to the directrix line.
The vertex is the point where the parabola changes direction from left to right.
The standard form equation of a parabola with vertex at the origin is y^2 = 4px for a parabola opening to the right, and x^2 = 4py for a parabola opening upward.
If p is positive, the parabola opens to the right or upward. If p is negative, it opens to the left or downward.
The focus of a parabola is at the point (p, 0) if it opens to the right, or (0, p) if it opens upward.
The length of the latus rectum (the chord that passes through the focus and is perpendicular to the directrix) is 4p.
The endpoints of the latus rectum are at (p, ±2p) if the parabola opens to the right or upward.
The axis of symmetry of a parabola is a vertical line passing through the vertex, with equation x = h.
The directrix is a fixed line that is perpendicular to the axis of symmetry, with equation x = -p/2 for a parabola opening to the right, or y = -p/2 for one opening upward.
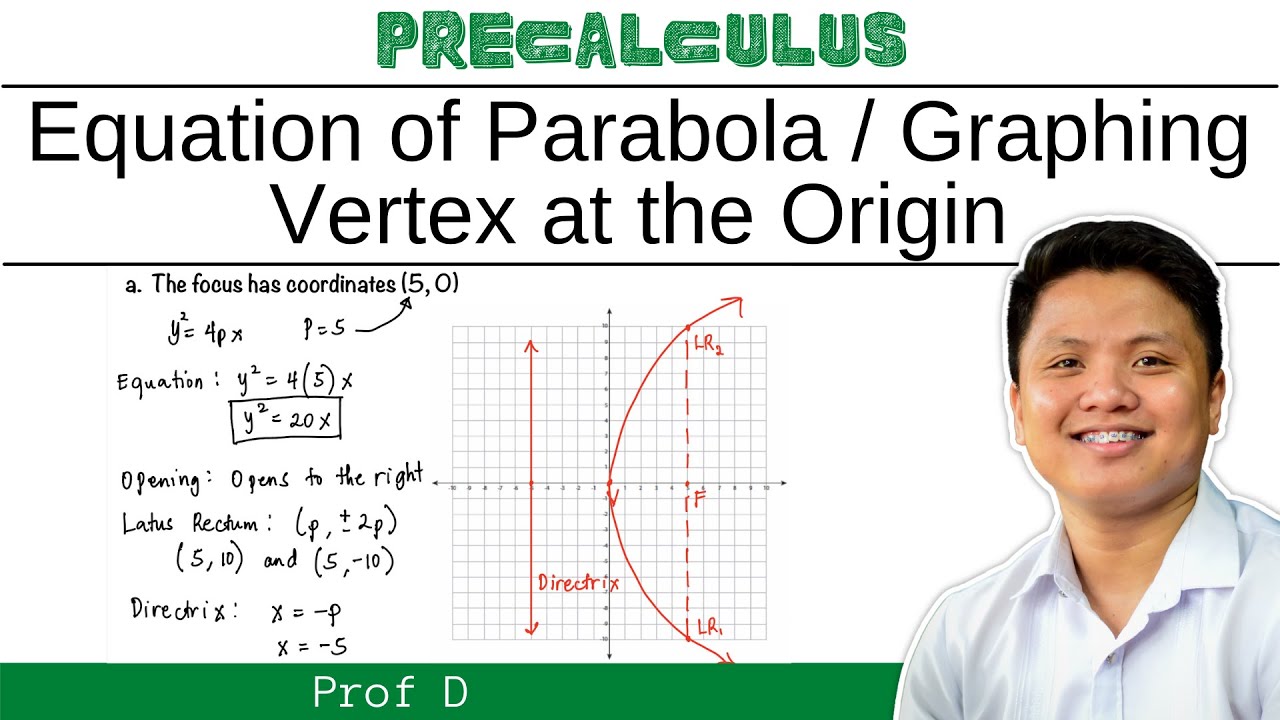
For a parabola with equation y^2 = 16x, the parabola opens to the right since p = 4 is positive. The focus is at (4, 0), the endpoints of the latus rectum are at (4, ±8), and the directrix is x = -4.
For a parabola with equation x^2 = 8y, it opens upward since p = 2 is positive. The focus is at (0, 4), the axis of symmetry is x = 0, and the directrix is y = -2.
For a parabola with equation y^2 = -10x, it opens to the left since p = -5/2 is negative. The focus is at (-5/2, 0), the endpoints of the latus rectum are at (-5/2, ±5), and the directrix is x = 5/2.
The axis of symmetry for all parabolas is either a vertical or horizontal line passing through the vertex.
The direction a parabola opens (left, right, up, down) depends on the sign and value of the parameter p in the standard form equation.
The focus, endpoints of the latus rectum, axis of symmetry, and directrix can all be determined algebraically from the standard form equation of a parabola.
Graphing a parabola involves identifying its key features - vertex, focus, directrix, latus rectum, and axis of symmetry - and using them to plot the curve.
Transcripts
Browse More Related Video
FINDING THE EQUATION OF THE PARABOLA | GRAPHING | VERTEX AT THE ORIGIN | PROF D

How to find the equation of a parabola given vertex and directrix | @ProfD

STANDARD FORM OF THE EQUATION OF A PARABOLA WITH VERTEX AT THE ORIGIN || PRE-CALCULUS
Ch. 11.1 Parabolas
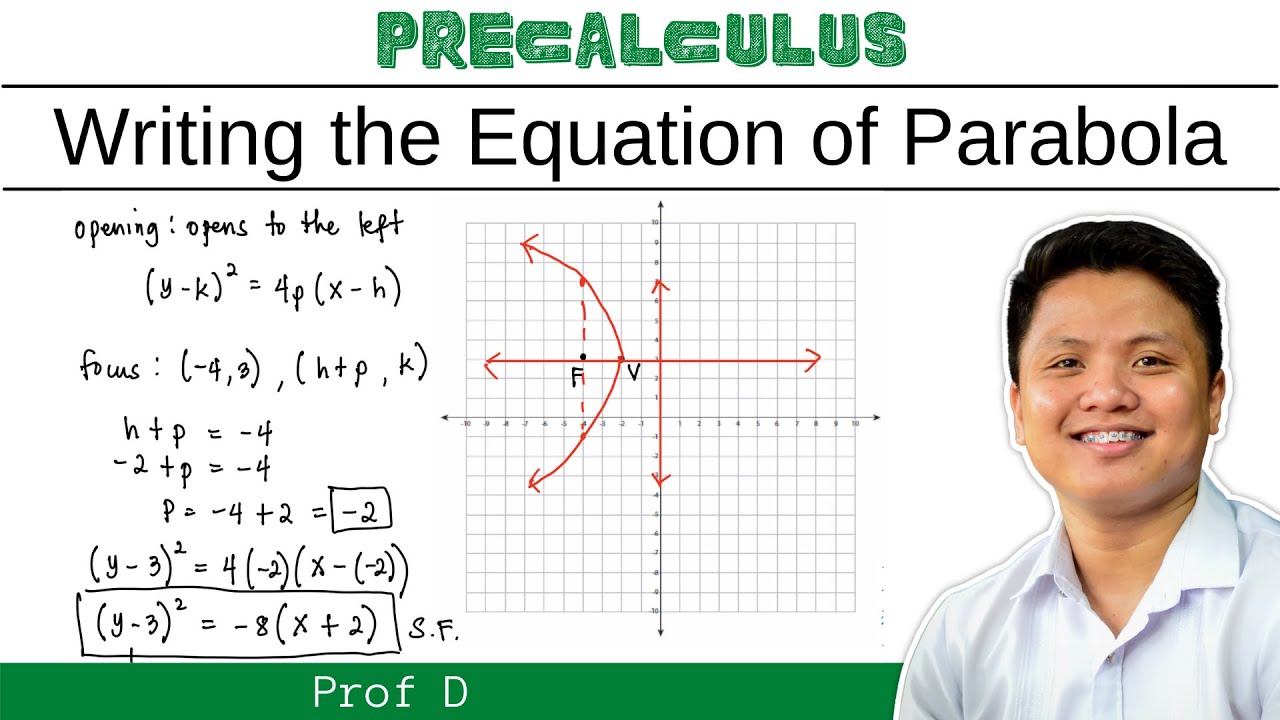
Writing Equation of A Parabola in Standard and General Form | @ProfD

Ch. 11.6 Polar Equations of Conics
5.0 / 5 (0 votes)
Thanks for rating: