Introduction to compound interest and e | Algebra II | Khan Academy

Khan Academy
22 Apr 200810:11
EducationalLearning
32 Likes 10 Comments

TLDRThe script narrates a scenario where a person borrows a dollar from a local loan shark at a 100% annual interest rate. The borrower is given the option to repay early, but this leads to compounding interest, where the principal increases with each period. The example illustrates how the effective annual rate increases from 100% to 125% when compounded semi-annually, and further to 166% when compounded monthly. The script uses simple math to demonstrate the exponential growth of debt due to compounding, highlighting the high costs of borrowing from loan sharks.

Takeaways
  • 📊 The script explains the concept of compounding interest using a hypothetical scenario with a local loan shark.
  • 💰 The loan shark offers a loan at an annual interest rate of 100%, meaning the borrower must pay back double the principal amount after one year.
  • 🕒 The borrower has the option to repay the loan earlier, with interest calculated on a prorated basis for the time the money was borrowed.
  • 🔢 If the loan is repaid in six months, the borrower pays back the principal plus 50% interest, resulting in a total repayment of $1.50.
  • 📈 The script illustrates how compounding works by showing that if the loan is not repaid after six months, the interest is calculated on the new principal amount, leading to higher total interest over time.
  • 🤔 The borrower is presented with different scenarios of repaying the loan earlier, with each scenario showing how compounding interest increases the total amount owed.
  • 📉 When considering monthly repayments, the interest rate is 8.5% per month, and the script demonstrates how this compounds to an effective annual interest rate of 166%.
  • 📚 The concept of daily compounding is introduced, with the loan shark offering to charge 0.27% daily interest, compounded over 365 days.
  • 🧮 The script uses mathematical calculations to show the exponential growth of the loan amount due to compounding, emphasizing the power of compound interest.
  • 💡 It highlights the importance of understanding the terms of a loan, especially the impact of compounding interest on the total amount that must be repaid.
  • 🚫 The loan shark scenario serves as a cautionary tale about the high costs of borrowing money from lenders with exorbitant interest rates.
Q & A

  • What is the annual interest rate offered by the local loan shark in the scenario?

    -The local loan shark offers a 100% annual interest rate on the loan.

  • If the borrower pays back in six months, what percentage of interest is charged?

    -If the borrower pays back in six months, a 50% interest is charged.

  • What is the total amount the borrower has to pay back after one year with the initial conditions?

    -After one year, the borrower has to pay back the principal of $1 plus the 100% interest, which totals $2.

  • How does the interest rate change if the loan is reborrowed after six months?

    -If the loan is reborrowed after six months, the interest rate remains at 50% for the next six months, but it is calculated on the new principal, which includes the initial principal and the interest accrued in the first six months.

  • What is the effective annual interest rate if the borrower has the option to pay earlier but chooses to pay after one year?

    -The effective annual interest rate, if the borrower pays after one year with the option to pay earlier, is approximately 125%.

  • What is the concept of compounding interest as explained in the script?

    -Compounding interest is the process where the interest is added to the principal at the end of each compounding period, and the new total becomes the principal for the next period's interest calculation.

  • If the loan is compounded monthly, what is the monthly interest rate and how does it affect the total amount owed after a year?

    -If the loan is compounded monthly, the monthly interest rate is 8.5%. After a year, the total amount owed is $2.66, which represents an effective interest rate of 166%.

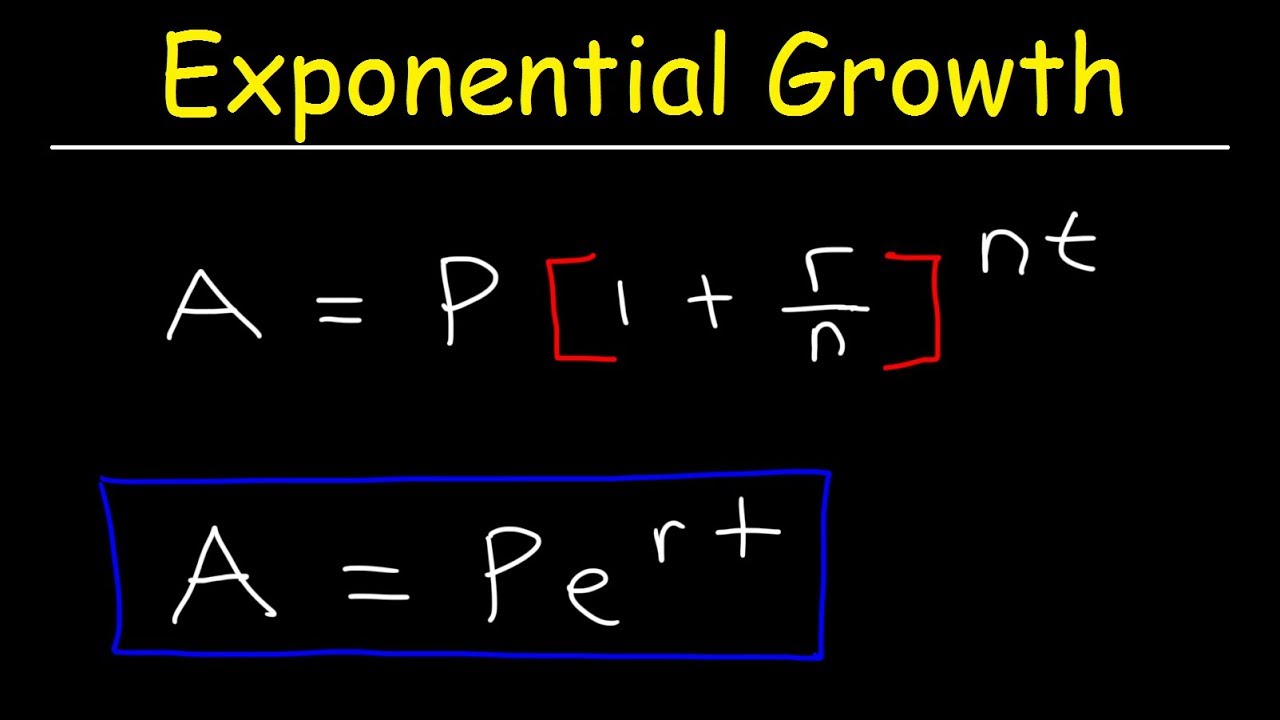
  • What is the formula for calculating the total amount owed when compounding interest n times a year?

    -The formula for calculating the total amount owed when compounding interest n times a year is the principal multiplied by (1 + (annual interest rate / n))^(n*t), where t is the time in years.

  • How does the effective interest rate change when the interest is compounded daily?

    -When the interest is compounded daily, the effective interest rate is higher than the annual rate due to the increased number of compounding periods. In the script, with a 100% annual interest rate compounded daily, the borrower would owe approximately $2.66 after a year.

  • Why does the local loan shark prefer not to allow early payment without reborrowing the money?

    -The local loan shark prefers not to allow early payment without reborrowing the money because it secures the opportunity to earn interest for the entire year, rather than losing the chance to invest or lend the money elsewhere for a shorter period.

  • What is the significance of the federal funds rate mentioned in the script?

    -The federal funds rate is mentioned to contrast with the high 100% interest rate offered by the local loan shark. It serves to highlight the exorbitant rate being charged compared to standard market rates.

Outlines
00:00
🤔 Understanding Loan Shark Interest Rates

This paragraph introduces a hypothetical scenario where the speaker plays the role of a local loan shark. It explains how interest rates work in this context, starting with a 100% annual interest rate on a $1 loan. The borrower is expected to pay back $2 after a year, which includes the principal amount plus the interest. The speaker also discusses the borrower's option to repay the loan earlier, which would result in paying only 50% interest after six months, amounting to $1.50. However, if the borrower cannot repay within six months, they would need to reborrow for another six months at the same 50% interest rate, leading to a total repayment of $2.25 after a year. The paragraph highlights the concept of principal and interest in finance and the implications of borrowing money at high interest rates.

05:00
📊 The Impact of Compounding Interest

In this paragraph, the concept of compounding interest is explored through the same loan shark scenario. The speaker explains how the interest rate can be compounded more frequently, such as twice a year, monthly, or even daily. Using the example of monthly compounding at an 8.5% monthly rate, the speaker calculates that the borrower would owe $2.66 after a year, which equates to an effective annual interest rate of 166%. The explanation includes mathematical calculations to demonstrate how the interest accumulates over time due to compounding. The paragraph emphasizes the significant impact that compounding can have on the total amount owed and the importance of understanding the terms of a loan before agreeing to it.

10:03
🕒 Compounding Daily: The Power of Daily Interest

The final paragraph of the script begins to discuss the scenario of compounding interest daily. The speaker calculates that with daily compounding at a rate of 0.27% per day, the borrower would owe an amount raised to the power of 365 after one year. Unfortunately, the paragraph is cut off before the speaker can complete the explanation and provide the final amount owed. This leaves the viewer with an incomplete understanding of the daily compounding scenario, but it suggests that the effect of compounding can be even more pronounced when applied on a daily basis.

Mindmap
Keywords
💡Loan Shark
A loan shark is an individual who offers loans at extremely high interest rates, often to those who cannot secure traditional bank loans. In the video's narrative, the speaker assumes the role of a local loan shark to illustrate the concept of interest rates and their impact on loan repayment. The term is used to set the scenario for discussing various types of interest calculations.
💡Principal
In finance, the principal refers to the original amount of money that is borrowed or invested. The script uses the term to explain that the borrower must repay the principal amount plus any interest accrued. For example, if someone borrows $1 at 100% interest, they must repay $1 (the principal) plus $1 of interest, totaling $2.
💡Interest Rate
The interest rate is the percentage of the principal that is charged by the lender to the borrower for the use of the money over a specified period. The video script discusses different interest rates such as 100% annual interest and how they affect the total repayment amount. The concept is central to the video's theme of explaining compound interest.
💡Compound Interest
Compound interest is the interest on a loan or deposit calculated based on both the initial principal and the accumulated interest from previous periods. The script explains how compounding works with different intervals (e.g., semi-annually, monthly, daily) and how it increases the total amount owed over time. The video uses the concept to show that the effective interest rate can be significantly higher than the nominal rate due to compounding.
💡Federal Funds Rate
The federal funds rate is the interest rate at which depository institutions lend balances to each other overnight. In the script, it is mentioned as a comparison to highlight the unusually high interest rate of 100% charged by the 'loan shark'. This term is used to emphasize the predatory nature of the loan being discussed.
💡Effective Interest Rate
The effective interest rate is the true cost of funds over the period of a loan or deposit, taking into account the compounding of interest. The video script calculates the effective interest rate by showing how the total repayment amount increases due to compounding, resulting in rates that appear much higher than the nominal rate.
💡Annual Percentage Rate (APR)
Although not explicitly mentioned in the script, the concept of APR is implied when discussing interest rates. The APR is the annualized interest rate charged on loans, which includes both the interest rate and other fees. The video's theme revolves around explaining how different compounding intervals affect the APR.
💡Repayment
Repayment refers to the act of paying back a loan, including both the principal and the interest. The script uses the term in various scenarios to illustrate how the timing and method of repayment can affect the total amount owed. The concept is integral to understanding the impact of interest rates and compounding on loans.
💡Semi-Annual
Semi-annual refers to a frequency of twice a year. In the context of the script, the term is used to describe how interest is compounded semi-annually, meaning the interest is calculated and added to the principal every six months. This compounding interval is one of the examples used to explain the effects of compound interest.
💡Daily Compounding
Daily compounding is the process of calculating interest on a daily basis and adding it to the principal. The script discusses the concept as an extreme example of compounding frequency, showing how the interest rate, when compounded daily, results in a significantly higher total repayment amount over a year.
💡Excel
Excel is a spreadsheet program often used for financial calculations and data analysis. In the script, the speaker mentions using Excel to calculate the compounded interest over a year, demonstrating the practical application of the software in financial scenarios. This term is used to show how one might calculate complex interest scenarios in real life.
Highlights

Introduction of a hypothetical scenario involving a local loan shark and a desperate borrower.

Explanation of borrowing $1 at a 100% annual interest rate.

Clarification of principal and interest rate in finance terms.

Calculation of repayment after one year with 100% interest.

Discussion of federal funds rate as a comparison to the loan shark's interest rate.

Option to pay off the loan early after six months at a reduced interest rate.

Implication of early repayment on the loan shark's business model.

Concept of reborrowing the money for another period with compounding interest.

Illustration of how compounding interest works with an example.

Calculation of the effective annual interest rate with compounding.

Introduction of the term 'compounding interest' and its commonality.

Exploration of different repayment scenarios with monthly compounding.

Mathematical breakdown of monthly compounding leading to a higher effective interest rate.

Demonstration of the exponential growth of compounding interest with daily compounding.

Conclusion of the video with a teaser for the continuation in the next video.

Transcripts

Browse More Related Video

Review of Compound Interest (Precalculus - College Algebra 65)

Compound interest and e (part 4) | Exponential and logarithmic functions | Algebra II | Khan Academy

Compound interest and e (part 2) | Exponential and logarithmic functions | Algebra II | Khan Academy

Compound Interest & Population Growth Word Problems - Logarithms

Compound Interest

Interest (part 2) | Interest and debt | Finance & Capital Markets | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Compound InterestLoan SharkInterest RateBorrowing MoneyFinancial EducationDebt TrapMoney LendingInterest CalculationFinancial RiskEconomic TheoryInvestment Strategy