Introduction to interest | Interest and debt | Finance & Capital Markets | Khan Academy
TLDRThe video script delves into the concept of interest, distinguishing between simple and compound interest. It begins by defining interest as 'rent on money' and illustrates this with an example of borrowing $100 with an agreement to pay back $110 after a year, where the $10 is the interest. The script explains that interest is often calculated as a percentage of the principal amount borrowed. It then contrasts simple interest, where the interest paid each year is a fixed percentage of the original principal, with compound interest, where the interest is calculated on the growing amount of principal plus interest from the previous year. The script uses a 10-year borrowing scenario to highlight the significant difference between the two types of interest, with compound interest resulting in a much larger final amount owed. The presenter encourages viewers to calculate compound interest themselves to gain a deeper understanding of the concept and its implications.
Takeaways
- 📚 Interest is essentially 'rent on money', a fee paid to keep money for a certain period.
- 💰 The principal is the original amount of money borrowed or invested.
- 🔢 Interest is often calculated as a percentage of the principal, representing the cost of borrowing money.
- 📈 Simple interest is calculated by taking the interest rate times the original principal, and this amount is added each year.
- 🔺 Compound interest differs from simple interest by taking the interest rate times the total amount owed at the beginning of each period, including previously accrued interest.
- 🔄 With compound interest, the principal amount increases each period because interest is calculated on the growing balance.
- 📊 Over time, the difference between simple and compound interest can be significant, leading to a much higher total amount owed with compound interest.
- 📝 An example given in the script shows that after 10 years, simple interest results in owing $200 on a $100 principal with 10% interest, while compound interest results in owing approximately $259.
- 🤔 The script encourages viewers to calculate compound interest themselves to better understand the concept and its implications.
- 👨🏫 The speaker plans to provide more examples in a follow-up video to deepen the understanding of compound interest and the workings of exponents.
- ⏰ The importance of understanding interest, particularly the difference between simple and compound interest, is highlighted as a potentially life-saving financial concept.
Q & A
What is the basic concept of interest discussed in the script?
-The script discusses interest as essentially 'rent on money', which is the money paid to keep money for a certain period of time. It's like a fee for borrowing money and using it as needed.
How is interest calculated in the context of the script?
-In the script, interest is calculated as a percentage of the original amount borrowed, known as the principal. For example, if you borrow $100 and the interest rate is 10%, you would pay $10 in interest.
What is the difference between simple interest and compound interest?
-Simple interest is calculated only on the original principal amount, with the same interest amount paid each year. Compound interest, however, is calculated on the initial principal plus any accumulated interest, causing the interest amount to grow larger each year.
In the script, what is the example given to illustrate simple interest?
-The script uses an example where if you borrow $100 at a 10% simple interest rate, after one year you would owe $110 ($100 principal + $10 interest), and after ten years, you would owe $200 ($100 principal + $100 interest).
How is compound interest demonstrated in the script?
-Compound interest is demonstrated by showing that if you borrow $100 at a 10% interest rate compounded annually, after one year you would owe $110, and in subsequent years, the interest is calculated on the new principal amount, which includes the previous interest.
What is the formula for calculating compound interest mentioned in the script?
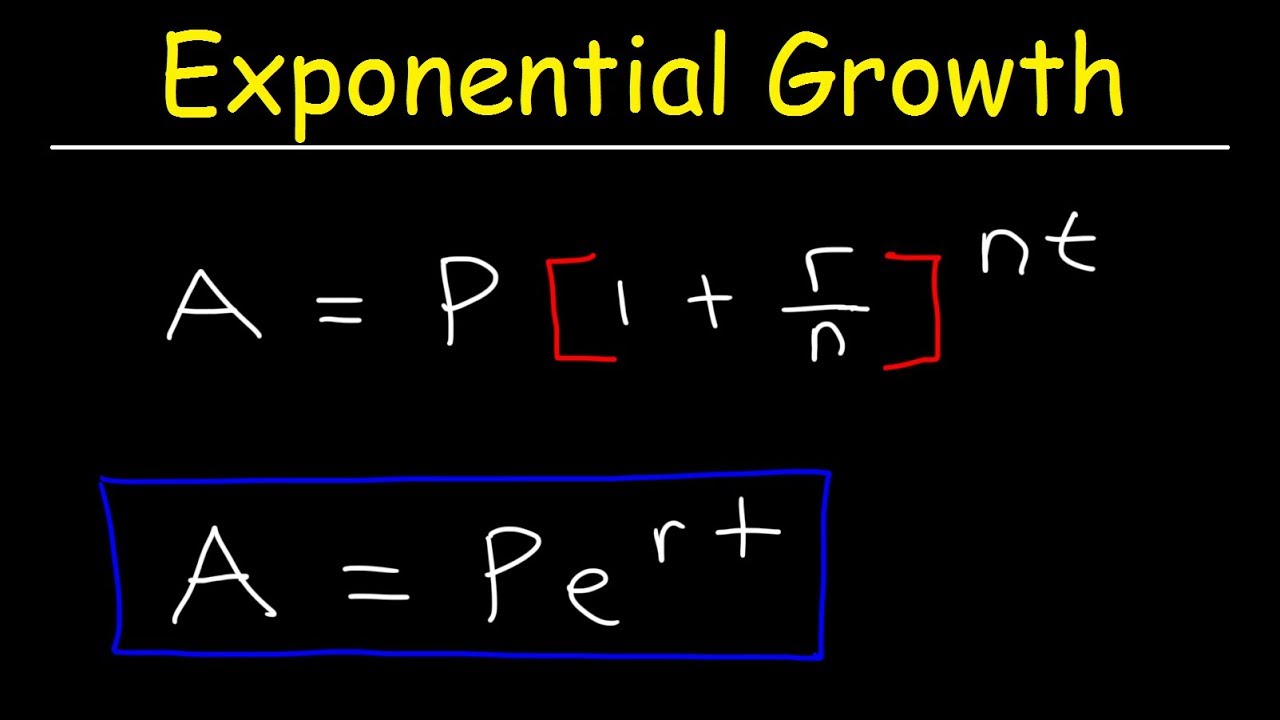
-The script mentions that the formula for calculating compound interest is P(1 + r/n)^(nt), where P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the time the money is invested or borrowed for in years. In the script's example, it simplifies to P * (1 + r)^t.
How much would you owe after 10 years if you borrowed $100 at a 10% compound interest rate according to the script?
-According to the script, if you borrowed $100 at a 10% compound interest rate, after 10 years you would owe approximately $259.
Why is understanding the difference between simple and compound interest important?
-Understanding the difference between simple and compound interest is important because it can significantly affect the total amount of money owed or earned over time. Compound interest can lead to a much larger sum due to the interest being compounded annually.
What is the principal amount in the context of the script's discussion on interest?
-In the script, the principal amount refers to the original sum of money that is borrowed or invested, which is then used as the base for calculating interest.
How does the script suggest one might avoid filing for bankruptcy?
-The script suggests that understanding the concept of interest, particularly the difference between simple and compound interest, can help one make informed financial decisions, potentially avoiding situations like bankruptcy.
What is the difference in the total amount owed after 10 years between simple and compound interest in the script's example?
-In the script's example, the difference in the total amount owed after 10 years between simple and compound interest is $59, with compound interest resulting in a higher amount owed ($259) compared to simple interest ($200).
Outlines
💡 Understanding Interest and Its Types
This paragraph introduces the concept of interest, which is described as a fee paid for the use of money over time. It distinguishes between simple and compound interest. The speaker uses an example of borrowing $100 and paying back $110 after one year to illustrate the idea of interest as 'rent on money.' The interest rate is applied as a percentage of the principal, which is the original amount borrowed. The paragraph also contrasts simple interest, where the interest is calculated on the original principal only, with compound interest, which will be explained in more detail in the next paragraph.
📊 Simple vs. Compound Interest Calculation
The second paragraph delves into the specifics of how simple and compound interest are calculated. Simple interest is demonstrated as an annual fee of $10 on a $100 loan, resulting in a total owed of $200 after 10 years. In contrast, compound interest is shown to accumulate more significantly over the same period. The speaker explains that with compound interest, the interest is calculated on the new principal amount each year, which includes the previous interest. This results in an exponential growth of the owed amount, culminating in an amount of approximately $259 after 10 years, highlighting the substantial difference between the two types of interest over time.
Mindmap
Keywords
💡Interest
💡Simple Interest
💡Compound Interest
💡Principal
💡Mortgage
💡Credit Card
💡Banker
💡Finance
💡Exponent
💡Spreadsheet
💡Bankruptcy
Highlights
Introduction to the concept of interest, a fundamental financial principle.
Interest defined as 'rent on money', emphasizing its role in borrowing.
Explanation of how interest is calculated as a percentage of the principal amount borrowed.
Illustration of simple interest calculation with an example of borrowing $100.
Clarification of the term 'principal' in the context of interest calculations.
Demonstration of how simple interest accumulates over time with a 10% annual rate.
Introduction of the concept of compound interest as opposed to simple interest.
Comparison between simple and compound interest using a 10-year borrowing period.
Mathematical representation of compound interest with the formula 100 * 1.1^n.
Explanation of how compound interest affects the total amount owed over time.
Highlighting the difference in total owed amount between simple and compound interest after 10 years.
The subtle but significant distinction between simple and compound interest calculations.
The impact of compound interest on long-term financial planning and debt.
The importance of understanding interest for personal finance and avoiding bankruptcy.
A promise of further examples and deeper understanding in the next video.
The practical application of interest concepts in everyday financial decisions.
Transcripts
Browse More Related Video

Interest (part 2) | Interest and debt | Finance & Capital Markets | Khan Academy

Compound interest and e (part 4) | Exponential and logarithmic functions | Algebra II | Khan Academy

Review of Compound Interest (Precalculus - College Algebra 65)

Compound Interest
Compound Interest & Population Growth Word Problems - Logarithms

Introduction to compound interest and e | Algebra II | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: