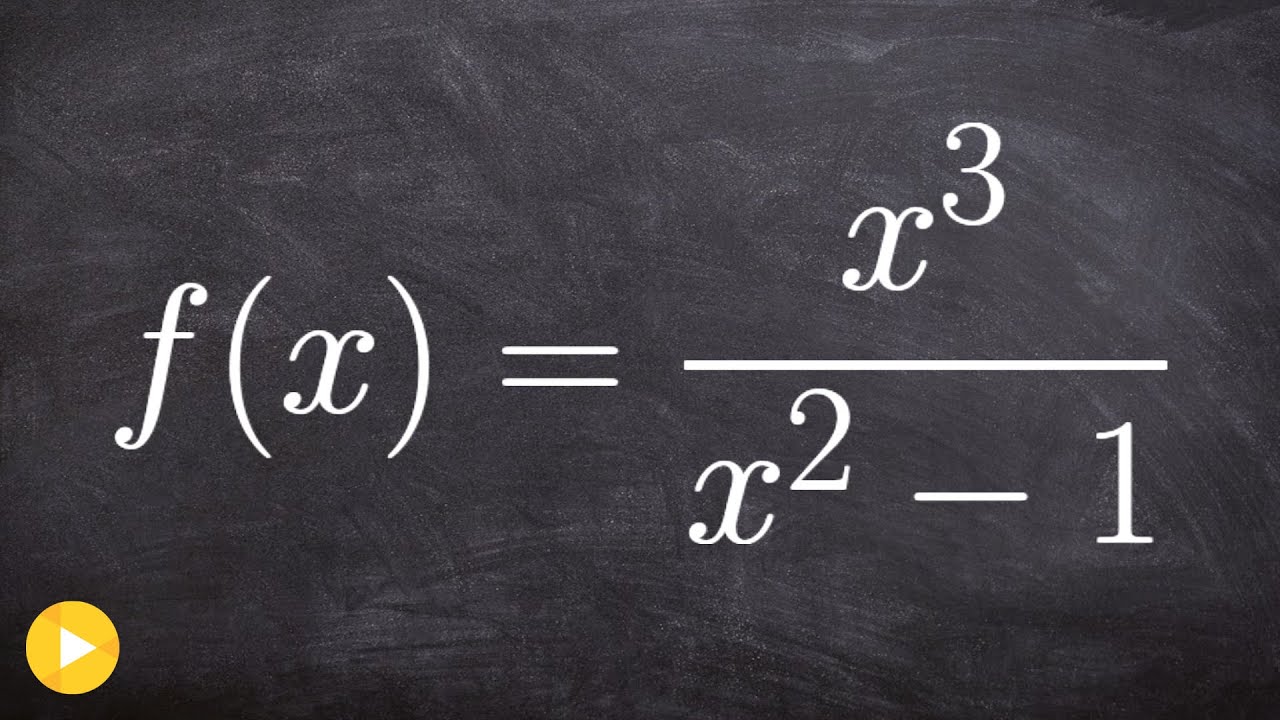How to divide a trinomial into a polynomial using long division
TLDRThis instructional video script explains the process of polynomial long division, emphasizing that it follows the same principles as regular division but requires special attention when the divisor is not linear. The instructor uses x squared as an example divisor and x to the fourth as the dividend, demonstrating each step of the division, including multiplying the quotient by the divisor and subtracting the result from the dividend. They also highlight common mistakes, particularly in subtraction, and suggest an alternative method of converting subtraction into addition to avoid errors. The final quotient is presented as x squared minus 4x plus 12, with a remainder over the divisor.
Takeaways
- 📚 The process of polynomial long division is similar to regular division, with the main difference being the divisor can be a polynomial, not just a single term.
- 🔍 When the divisor is a polynomial, long division is used instead of synthetic division, which is reserved for linear divisors.
- 📝 The first term of the divisor is used to determine how many times it divides into the dividend, starting the quotient.
- 🔢 The quotient is developed by multiplying the result of the division by the first term of the divisor and subtracting it from the dividend.
- ✅ The rules of exponents apply when determining how many times a term divides into another, such as x^2 dividing x^4 resulting in x^2.
- 🔄 The process is iterative, with each new term in the quotient being multiplied by the entire divisor and subtracted from the current dividend.
- 👍 A positive approach to subtraction can be used to avoid common mistakes by rewriting subtraction as addition of a negative term.
- 📉 It's important to keep track of signs, especially when converting subtraction into addition with negative terms.
- 📝 The final quotient will include the terms derived from the division process, with any remainder indicated over the original divisor.
- 🤔 The instructor emphasizes the importance of understanding the division process and suggests writing out steps for clarity.
- 💡 The script provides a practical approach to long division, including tips for avoiding common errors and ensuring accuracy.
Q & A
What is the primary difference between the division process discussed in the script and previous examples?
-The primary difference is that the divisor is no longer a single term but a polynomial with multiple terms, requiring the use of long division instead of synthetic division.
Why is long division necessary when the divisor is not linear?
-Long division is necessary when the divisor is a polynomial raised to a power higher than one, such as a quadratic or higher, because it involves dividing by multiple terms.
What is the significance of using only the first term of the divisor in the division process?
-The first term of the divisor is used to determine the initial part of the quotient. This is because the division process involves dividing the leading term of the dividend by the leading term of the divisor.
How does the process of dividing x^4 by x^2 using the rules of exponents?
-According to the rules of exponents, x^4 divided by x^2 is x^(4-2), which simplifies to x^2.
What is the purpose of multiplying the quotient by each term of the divisor?
-Multiplying the quotient by each term of the divisor is necessary to perform the division process step by step, ensuring that each term of the dividend is accounted for in the division.
Why is it recommended to rewrite subtraction as addition when performing long division?
-Rewriting subtraction as addition can help prevent mistakes, as many students struggle with subtraction during the division process. Changing the signs and performing addition can simplify the process.
What is the common mistake students make when subtracting during long division, according to the script?
-The common mistake is errors in the subtraction process, which can lead to incorrect results in the division.
How does the script suggest handling the remainder after performing the division process?
-The remainder is brought down when needed and included in the final quotient expression, typically written as 'remainder over divisor'.
What is the final quotient in the example problem discussed in the script?
-The final quotient in the example is x^2 - 4x + 12, with a remainder over the divisor.
How can the process of long division be made easier according to the script?
-The script suggests changing subtraction into addition by changing the signs of terms, which can make the division process easier and help avoid common mistakes.
Outlines
📚 Polynomial Long Division Basics
This paragraph introduces the fundamental concept of polynomial long division, emphasizing that the process remains consistent with basic division, but with a polynomial divisor. The focus is on using the first term of the divisor to divide into the dividend and obtaining a quotient. The explanation includes a step-by-step guide on how to perform the division, starting with identifying how many times the divisor, in this case, x squared, fits into the dividend, x to the fourth, and then multiplying the resulting quotient by each term of the divisor. The paragraph also addresses common mistakes made during the subtraction step of the division process.
🔍 Advanced Polynomial Long Division Techniques
The second paragraph delves deeper into the long division of polynomials, particularly when dealing with terms beyond linear. It explains the importance of using the first term of the divisor and how to handle the subtraction process to avoid common errors. The instructor suggests an alternative method to subtraction by converting it into an addition problem with negative terms, which can simplify the process and reduce mistakes. The paragraph provides a detailed example of dividing a cubic term by a quadratic term, demonstrating the multiplication of the quotient by the divisor and the subsequent subtraction to arrive at the next term in the quotient. The summary of the process includes the correct quotient and remainder, highlighting the importance of careful calculation to avoid errors.
Mindmap
Keywords
💡Long Division
💡Divisor
💡Dividend
💡Quotient
💡Polynomial
💡Synthetic Division
💡Exponents
💡Subtraction
💡Multiplication
💡Remainder
Highlights
The process remains the same for division; we still use a divisor, a dividend, and we get a quotient.
If the divisor is a single term, we can use synthetic division, but for polynomials of higher degrees, long division is required.
When dividing by a polynomial, we focus on the first term of the divisor for each step.
To determine how many times x squared divides into x to the fourth, use the rules of exponents: x to the 4 minus 2 equals x squared.
Multiply the quotient term by every term of the divisor to proceed with long division.
Subtracting polynomials can be tricky, so rewriting subtraction as addition by changing the signs can help avoid mistakes.
After each subtraction, bring down the next terms only when needed to continue the division process.
Rewriting the problem as an addition problem by distributing the negative sign simplifies the process and reduces errors.
In long division, focus on the leading term of the divisor for each step of the division.
Negative times negative results in a positive, and this principle helps in correctly multiplying terms.
Adding the negative of a term is equivalent to subtraction, which can simplify the arithmetic.
When dividing x squared into higher-degree terms, write it out to avoid mistakes in exponent rules.
After finding each quotient term, multiply it through the entire divisor to form the new polynomial to subtract.
Subtraction mistakes are common, so verifying each step carefully is crucial.
The final quotient includes the remainder divided by the original divisor, completing the division process.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: