Finding ALL Solutions of Polynomials (Precalculus - College Algebra 37)

Professor Leonard

29 Sept 202069:17

EducationalLearning

32 Likes 10 Comments

TLDRThis comprehensive video script delves into the intricacies of finding zeros or solutions to polynomials, including those with complex solutions. The presenter guides viewers through a multi-faceted approach, starting with contrived examples that introduce complex solutions like 2i, and then progressively moving towards more conventional methods. Emphasis is placed on the importance of factoring, synthetic division, and the application of the rational zeros theorem. The script meticulously explains how to handle polynomials of varying degrees, especially fourth-degree polynomials, which are guaranteed to have four solutions or factors. It also touches on the use of the quadratic formula for irreducible quadratics and the concept of complex conjugate pairs in finding zeros. The presenter further illustrates the process of long division with polynomials, highlighting common mistakes and providing clear instructions to avoid them. The video is an invaluable resource for anyone looking to strengthen their understanding of polynomial solutions, factoring techniques, and the application of mathematical theorems in a step-by-step manner.

Takeaways

📚 Start by finding a zero if given, otherwise use the Rational Zeros Theorem to find potential zeros.
🔍 If a real zero is found, create a linear factor and use synthetic division to simplify the polynomial.
🌟 Complex zeros always come in conjugate pairs, so finding one gives you another for free.
🔗 Use the zero product property to convert zeros into factors, which can then be distributed to form irreducible quadratic factors.
📉 For complex factors, perform long division to divide out the factors and simplify the polynomial further.
🔢 The degree of a polynomial dictates the maximum number of real solutions and the exact number of complex solutions.
🔍 Use the Cardano's rule of signs to predict the number of positive and negative real roots.
📝 When a polynomial is not easily factorable, apply the quadratic formula to find real or complex solutions.
🔄 Always check for factorability before resorting to the Rational Zeros Theorem or quadratic formula, as factoring is often quicker.
🧮 Synthetic division works with both whole numbers and fractions, and can be used to find factors of a polynomial.
🔑 The process of solving polynomials involves a combination of factoring, synthetic division, and applying the quadratic formula, depending on the nature of the polynomial.

Q & A

What is the main topic of the video?
-The main topic of the video is finding all the zeros or solutions to a polynomial, including complex solutions, through various methods and examples.
What is the significance of a polynomial's degree in relation to its solutions?
-The degree of a polynomial is significant because it determines the number of solutions or zeros the polynomial has. For instance, a polynomial of degree 3 will have exactly three solutions, which may be real or complex.
What is the Rational Zeros Theorem mentioned in the video?
-The Rational Zeros Theorem is a method used to find potential rational zeros of a polynomial. It states that if a polynomial has a rational zero, it must be of the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient.
How can complex solutions be identified in a polynomial?
-Complex solutions can be identified by using the property that they come in conjugate pairs. If a complex number is a solution, its conjugate is also a solution. This is particularly useful when the polynomial has an even degree and no real solutions are found initially.
What is the process of long division of polynomials and when is it used?
-Long division of polynomials is a method used to divide a polynomial by another polynomial of lower degree to find the quotient and the remainder. It is used when dealing with irreducible quadratic factors or when synthetic division is not applicable, such as with complex numbers.
How does the concept of factoring play a role in solving polynomials?
-Factoring plays a crucial role in solving polynomials as it allows us to break down complex polynomials into simpler expressions, making them easier to analyze and solve. Factoring can reveal the zeros of the polynomial and is often the quickest method to find solutions when possible.
What is the difference between synthetic division and long division in the context of solving polynomials?
-Synthetic division is a shorthand method of dividing a polynomial by a linear factor to find the quotient, and it is faster than long division. Long division, on the other hand, can be used to divide a polynomial by any factor, including quadratic factors, and is necessary when dealing with complex or irreducible quadratic factors.
What is the significance of the zero product property in solving polynomials?
-The zero product property states that if the product of two factors is zero, then at least one of the factors must be zero. This property is used to set each factor of a polynomial equal to zero in order to find the zeros or solutions of the polynomial.
How does the video demonstrate the use of the quadratic formula in solving polynomials?
-The video demonstrates that the quadratic formula is used when a quadratic factor of a polynomial cannot be factored further, or when dealing with irreducible quadratic factors. It provides solutions, which can be real or complex, depending on the discriminant of the quadratic equation.
What is the role of the Card's Rule of Signs in the process of finding solutions to a polynomial?
-Card's Rule of Signs is a technique used to determine the number of positive and negative real roots of a polynomial. It helps in narrowing down the potential rational zeros and guides the process of testing possible solutions, thus saving time and effort.

Outlines

00:00

😀 Introduction to Finding Polynomial Zeros

The video begins with an introduction to finding zeros of polynomials, including complex solutions. The presenter plans to cover six examples, starting with two that involve complex solutions. The goal is to teach viewers how to perform long division of polynomials without a linear factor, focusing on quadratic factors. The importance of this skill for advanced topics like calculus is highlighted.

05:01

📚 Complex Zeros and Polynomial Long Division

The presenter explains how to deal with complex zeros in polynomials and the process of long division. They demonstrate how complex conjugate pairs are used to create linear factors, which are then distributed to form an irreducible quadratic factor. The process is illustrated through the division of a cubic polynomial by a quadratic factor, emphasizing the importance of placeholders and correct term matching.

10:02

🔍 Identifying and Factoring Polynomials

The video continues with the process of identifying zeros and factoring polynomials. It is shown how to use the rational zeros theorem to find zeros and then create factors from real or complex zeros. The presenter also discusses the concept of irreducible quadratics and the application of long division to simplify polynomials, leading to finding all zeros of a polynomial.

15:03

🔢 Dealing with Complex Conjugate Pairs

The focus shifts to handling complex conjugate pairs in polynomials. The presenter explains that complex zeros always come in pairs and demonstrates how to build factors from these pairs. They also show how to simplify the process by grouping terms and using the properties of complex conjugates to create an irreducible quadratic factor.

20:22

📈 Polynomial Reduction and Factoring

The presenter illustrates how to reduce a polynomial by dividing it by a known factor, which results in a quotient that can be further factored. They emphasize the importance of ensuring the remainder is zero after division, indicating that the division has been performed correctly. The process of factoring over the real and complex number systems is also discussed.

25:35

🤔 Factoring Over the Real Number System

The video addresses the process of factoring polynomials over the real number system. The presenter explains how to handle irreducible quadratics and when to apply the quadratic formula. They also discuss the uniqueness of factoring and the importance of considering all possible factors, including complex solutions.

30:36

🧮 Rational Zeros Theorem and Polynomial Factoring

The presenter concludes with a discussion on the rational zeros theorem and its application in finding zeros of a polynomial. They provide a comprehensive guide on how to use the theorem to generate a list of possible zeros, and then apply synthetic division to find factors. The video emphasizes the importance of factoring and the various techniques used to find real and complex zeros of polynomials.

Mindmap

Keywords

💡Polynomial

A polynomial is a mathematical expression involving a sum of powers in a single variable, x. It is the central theme of the video as the script discusses finding zeros or solutions to polynomials, which are crucial for understanding their behavior and graphing. The video covers polynomials of degree three and four, illustrating how to find their solutions, including real and complex ones.

💡Zeroes or Solutions

In the context of the video, zeroes or solutions refer to the values of x that make the polynomial equal to zero. The video's primary goal is to find these values, which can be real or complex numbers. The script mentions that a polynomial of degree three will always have three solutions, which might be real or complex, including multiplicity.

💡Complex Solutions

Complex solutions are solutions to polynomial equations that involve imaginary numbers, denoted by the symbol 'i'. The video explains that complex solutions always come in conjugate pairs, which is a key concept when solving polynomials with no real solutions. The script illustrates how to find and use complex solutions through examples like 'x^3 - 4x^2 + 4x - 16' with a given complex solution of 2i.

💡Rational Zeros Theorem

The Rational Zeros Theorem is a method used to find possible rational solutions to a polynomial equation. It is mentioned in the script as a technique for guessing and checking potential zeros when no zeros are initially given. The theorem states that any rational solution to a polynomial equation can be expressed as a fraction of the factors of the constant term divided by a factor of the leading coefficient.

💡Synthetic Division

Synthetic division is a shortcut method for dividing a polynomial by a linear factor. The video demonstrates its use in finding other factors of the polynomial once one zero is known. It is a crucial technique for reducing the polynomial's degree and simplifying the process of finding remaining zeros or factors.

💡Long Division

Long division of polynomials is a process used to divide one polynomial by another to find a quotient and a remainder. In the video, it is used to divide the original polynomial by the factors obtained from complex solutions to get an irreducible quadratic factor. The script emphasizes its importance in cases where synthetic division is not applicable, such as with irreducible quadratic factors.

💡Irreducible Quadratic Factor

An irreducible quadratic factor is a quadratic expression that cannot be factored further using real numbers. In the context of the video, after obtaining complex solutions, the script shows how to create an irreducible quadratic factor from the complex linear factors and then divide the polynomial by this quadratic to find remaining factors or zeros.

💡Factoring

Factoring is the process of breaking down a polynomial into its simplest components, or factors. The video emphasizes the importance of factoring as a technique to simplify the process of finding zeros of a polynomial. It is shown as a preferred method when possible, as it is more efficient than applying the rational zeros theorem or using synthetic division with complex numbers.

💡Zero Product Property

The Zero Product Property states that if a product of factors equals zero, then at least one of the factors must be zero. The video uses this property to find the zeros of polynomials by setting factors equal to zero and solving for x. It is a fundamental concept in the process of finding real and complex zeros of polynomial equations.

💡Quadratic Formula

The quadratic formula is a method used to find the solutions of a quadratic equation. The script discusses its use when a quadratic equation cannot be factored. It provides a general solution involving the square root of the discriminant (b^2 - 4ac). The video mentions that the quadratic formula can yield either real or complex solutions, depending on the value under the square root.

💡Multiplicity

Multiplicity refers to the number of times a solution appears as a root of a polynomial. The video discusses how to determine the number of times a polynomial crosses the x-axis at a particular root, which is related to its multiplicity. A root with multiplicity one indicates a simple crossing, while higher multiplicities can indicate more complex behavior at that root.

Highlights

The video aims to find all zeros of a polynomial, including complex solutions, through six examples.

The presenter admits the first two examples are contrived to demonstrate complex solutions.

The importance of not forgetting about factoring when solving polynomials is emphasized.

The video teaches how to perform long division of polynomials with an irreducible quadratic factor.

For a degree 3 polynomial, there will always be exactly three solutions, which might include complex numbers.

The process of finding zeros involves using the rational zeros theorem and synthetic division.

The concept of complex conjugate pairs in polynomial solutions is explained.

The video demonstrates how to handle missing terms when distributing complex factors.

The presenter shows how to deal with special irreducible quadratics that lack a middle term.

An example of dividing a polynomial by a factor derived from complex linear factors is provided.

The process of factoring a quartic polynomial (degree four) is thoroughly explained.

The video covers how to handle polynomials that are not factorable using the quadratic formula.

The use of substitution, such as setting u = x^2, is introduced for certain polynomials.

The presenter discusses the application of the zero product property to find zeros of polynomials.

The video concludes with a comprehensive approach to solving polynomials, including complex and real solutions.

The importance of considering factoring before applying the rational zeros theorem is stressed.

The video provides a step-by-step guide on using synthetic division to find polynomial factors.

The process of solving for zeros of irreducible quadratics using the quadratic formula is demonstrated.

Transcripts

Browse More Related Video

Introduction to Complex Solutions of Polynomials (Precalculus - College algebra 35)

Creating Polynomials from Complex Solutions (Precalculus - College Algebra 36)

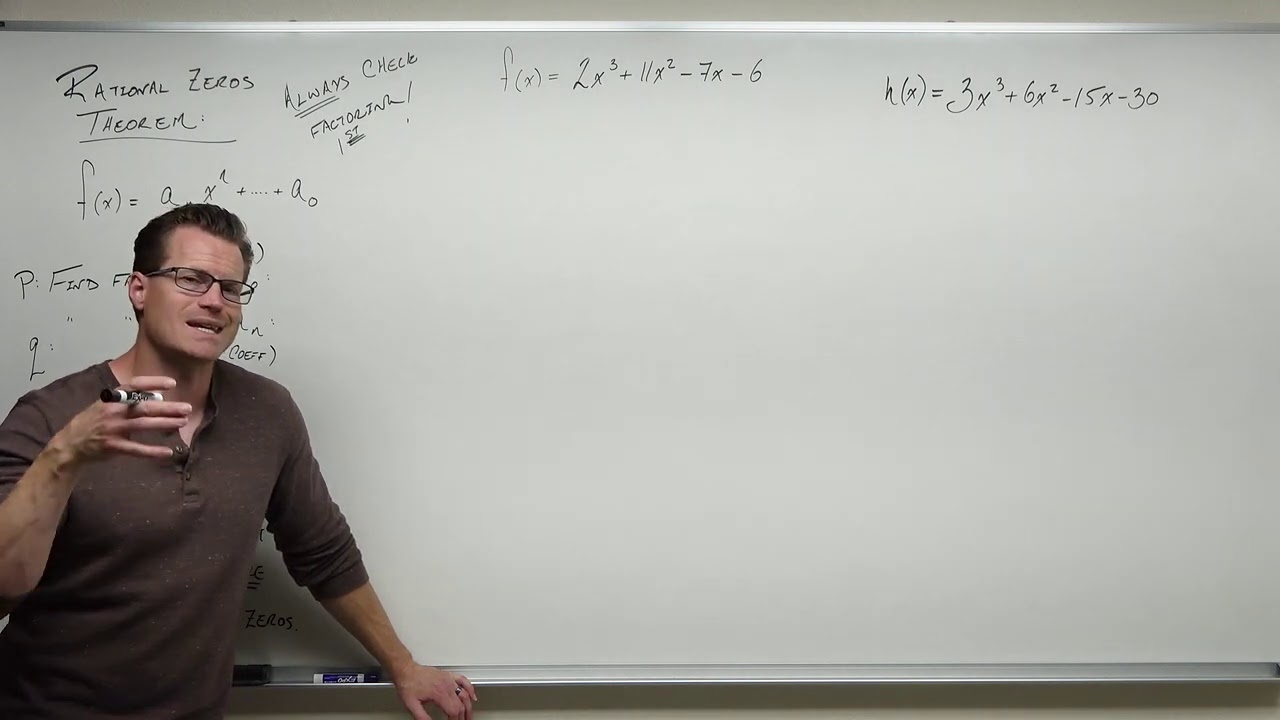
How to Use the Rational Zeros Theorem (Precalculus - College Algebra 34)

Synthetic Division and Long Division of Polynomials (Precalculus - College Algebra 32)

Solving Higher-Degree Polynomials by Synthetic Division and the Rational Roots Test

Solving Polynomial Equations By Factoring and Using Synthetic Division

Related Tags

Polynomial Zeros Complex Solutions Long Division Synthetic Division Rational Zeros Theorem Factoring Techniques Algebraic Concepts Mathematical Analysis Educational Content Calculus Preparation Polynomial Factorization