Understanding Degrees of Freedom

Lesics
7 Apr 201304:41
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the pivotal concept of degrees of freedom in kinematics, which is essential for understanding how many variables are needed to determine the position of a mechanism in space. This concept is crucial for anyone studying or working in the field of robotics, mechanical engineering, or any area where spatial positioning of mechanisms is critical. The script aims to provide clarity on this fundamental principle, offering insights that can help in the design and analysis of various mechanical systems.

Takeaways
  • 🧩 Degrees of freedom (DOF) is a crucial concept in kinematics.
  • 📏 DOF refers to the number of variables needed to specify the position of a mechanism in space.
  • 🔍 Understanding DOF is essential for analyzing and designing mechanical systems.
  • 🤖 In robotics, DOF determines the range of motion and capabilities of a robot.
  • 🔬 It is a fundamental parameter in the study of kinematic chains.
  • 🚀 DOF plays a significant role in aerospace engineering for satellite and spacecraft positioning.
  • 🏗️ In civil engineering, it impacts the design and stability of structures.
  • 🔄 DOF is also relevant in the field of biomechanics, analyzing human and animal movement.
  • 📐 The concept of DOF is used to calculate and predict the motion of various mechanisms.
  • 🛠️ Engineers must consider DOF when designing mechanisms to ensure they meet functional requirements.
  • 🔑 A higher DOF can provide more complex and precise movements but may also increase complexity and cost.
Q & A

  • What is the concept of degrees of freedom in kinematics?

    -Degrees of freedom in kinematics refers to the number of independent parameters or variables needed to define the position and orientation of a mechanism in three-dimensional space.

  • How does the number of degrees of freedom impact the movement of a mechanism?

    -The number of degrees of freedom determines the complexity of the motion a mechanism can perform. More degrees of freedom allow for more complex and versatile movements.

  • What are the three primary variables required to determine the position of an object in space?

    -The three primary variables required to determine the position of an object in space are its x, y, and z coordinates, which define its location along three orthogonal axes.

  • Can you explain the role of orientation in the degrees of freedom of a mechanism?

    -Orientation is crucial because, in addition to position, it determines how the mechanism is aligned in space. This is typically described by three additional variables, such as pitch, yaw, and roll, or using a set of Euler angles or a quaternion.

  • How does the concept of degrees of freedom apply to robotic arms?

    -In robotics, the degrees of freedom of an arm determine its range of motion and the precision with which it can interact with its environment. Each joint that can move independently contributes one degree of freedom.

  • What is the minimum number of degrees of freedom required to move an object freely in space?

    -An object needs a minimum of six degrees of freedom to move freely in space: three for translation (up/down, left/right, forward/backward) and three for rotation (pitch, yaw, roll).

  • How do constraints affect the degrees of freedom of a system?

    -Constraints reduce the degrees of freedom of a system by limiting the possible movements or positions that the system can take. For example, a fixed hinge reduces the rotation freedom of a mechanical arm.

  • What is the relationship between degrees of freedom and the complexity of control algorithms in robotics?

    -As the degrees of freedom increase, the complexity of the control algorithms required to manage the movement of a robotic system also increases, due to the greater number of variables that need to be coordinated.

  • Can you provide an example where a higher number of degrees of freedom is beneficial?

    -In precision assembly or surgery, a higher number of degrees of freedom allows for more nuanced and intricate movements, which can lead to better accuracy and control over the task being performed.

  • What is the term used to describe the reduction in degrees of freedom due to symmetry or repetitive structures?

    -The term is 'degeneracy'. It refers to the situation where the degrees of freedom are reduced because of symmetrical or repetitive elements in the mechanism, which can simplify the control and analysis.

  • How are degrees of freedom considered in the design of mechanical systems?

    -Designers of mechanical systems consider degrees of freedom to ensure that the system can perform the required tasks. They balance the need for sufficient freedom of movement with the complexity and cost of control systems.

  • What is the significance of understanding degrees of freedom in the field of biomechanics?

    -In biomechanics, understanding the degrees of freedom is essential for analyzing and replicating natural movements. It helps in designing prosthetics, orthotics, and in the study of human or animal motion.

Outlines
00:00
🔍 Degrees of Freedom in Kinematics

The first paragraph introduces the concept of 'degrees of freedom' as a pivotal aspect of kinematics. It explains that degrees of freedom refer to the number of independent variables necessary to specify the position of a mechanism in three-dimensional space. This fundamental concept is crucial for understanding how mechanisms move and function within their operational environment.

Mindmap
Keywords
💡Degrees of Freedom
Degrees of freedom in kinematics refers to the number of independent parameters that determine the position and orientation of a mechanism in space. It is a fundamental concept because it quantifies the complexity of motion a mechanism can have. In the context of the video, it is likely used to explain how many variables are needed to fully describe the motion of a mechanical system, which is crucial for designing and analyzing mechanisms.
💡Kinematics
Kinematics is a branch of classical mechanics that deals with the motion of points, bodies, and systems of bodies without considering the forces that cause the motion. It is a foundational concept for understanding how objects move and interact. In the video, kinematics is the overarching theme, with the degrees of freedom being a key aspect of analyzing and predicting motion within this field.
💡Variables
In the context of the video, variables are the different types of data points or parameters that can influence the motion of a mechanism. They are essential for calculating the degrees of freedom, as each variable represents a different aspect of motion that needs to be accounted for. The script implies that understanding these variables is critical for determining the position of a mechanism in space.
💡Mechanism
A mechanism, in the context of the video, refers to a device or system that performs a specific function through its motion. It could be a simple lever or a complex robotic arm. The term is used to illustrate the subject matter of the video, which is the study of how these mechanisms move and the factors that determine their motion.
💡Position
Position is a key concept in kinematics and refers to the location of a point or object in space. It is often described by coordinates and is essential for understanding the spatial arrangement of mechanisms. In the video, determining the position of a mechanism is directly related to calculating its degrees of freedom.
💡Space
Space, in this context, refers to the three-dimensional environment in which the mechanism exists and moves. It is the backdrop against which the kinematics of the mechanism are analyzed. The script suggests that the degrees of freedom are necessary to determine how a mechanism's position can vary within this spatial context.
💡Determine
To determine, in the context of the video, means to ascertain or establish the exact nature or position of something. It is used to describe the process of calculating or figuring out the degrees of freedom required for a mechanism. The script implies that this process is essential for understanding and controlling the motion of mechanisms.
💡Independence
Independence, in relation to degrees of freedom, refers to the lack of constraint between the variables that define the motion of a mechanism. These independent parameters can vary freely without affecting each other. The concept is important in the video's theme as it helps to distinguish between degrees of freedom that are truly independent and those that are not.
💡Parameters
Parameters are the specific values or characteristics that define a system or its behavior. In kinematics, parameters are used to describe the motion of a mechanism, such as its speed, direction, or acceleration. The script suggests that understanding these parameters is key to calculating the degrees of freedom.
💡Complexity
Complexity, in the context of the video, refers to the level of intricacy or the number of variables involved in the motion of a mechanism. A higher degree of complexity implies a greater number of degrees of freedom. The script likely uses this term to discuss how different mechanisms can have varying levels of complexity in their motion.
Highlights

Degrees of freedom is a crucial concept in kinematics.

It defines the number of variables needed to determine the position of a mechanism in space.

Understanding degrees of freedom is key to analyzing the motion capabilities of mechanisms.

Degrees of freedom can vary depending on the complexity of the mechanism.

It is essential for designing mechanisms with specific motion requirements.

The concept applies to both simple and complex mechanical systems.

Degrees of freedom can be calculated using mathematical models.

It is a fundamental aspect of robotic design and motion planning.

The concept helps in determining the range of motion for robotic arms.

It is also relevant in the field of biomechanics for understanding human movement.

Degrees of freedom is a critical parameter in the study of kinematic chains.

It influences the design and functionality of mechanical linkages.

The concept is vital for optimizing the performance of machines.

It is used to ensure that mechanisms can achieve desired positions and orientations.

Degrees of freedom is a measure of the mobility of a mechanism.

It is a key factor in the development of autonomous vehicles.

The concept plays a role in the design of prosthetic limbs for enhanced mobility.

Degrees of freedom is a fundamental concept in the field of kinematics with practical applications across various industries.

Transcripts

Browse More Related Video

Lecture 16: 10 Numerical Problems on Degrees of Freedom/Mobility of Planar Mechanisms | Kutzback |

Understand prismatic joint and how it affects the degrees of freedom in a system

Isotope Notation

Advanced Quantum Mechanics Lecture 6

what are degrees of freedom?

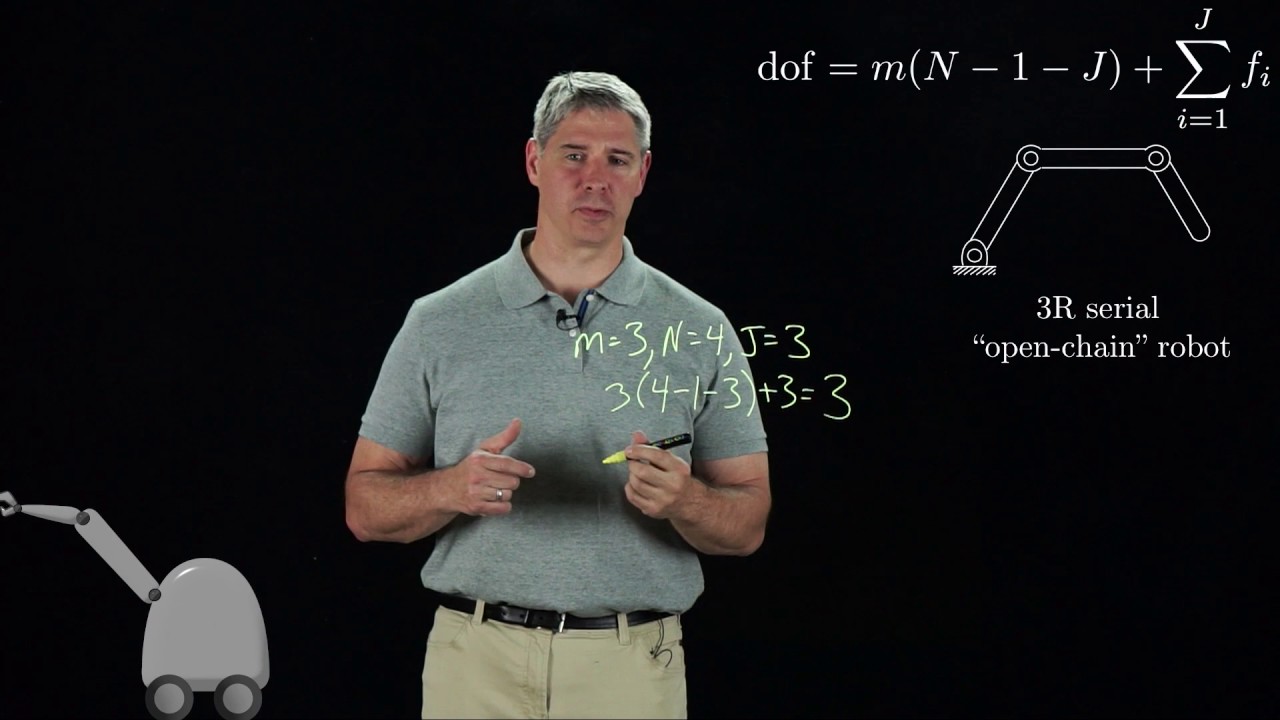
Modern Robotics, Chapter 2.2: Degrees of Freedom of a Robot

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Degrees of FreedomKinematicsMechanism PositionSpatial DeterminationMechanical EngineeringMotion AnalysisRoboticsEngineering PrinciplesDesign ConstraintsSpatial Geometry