Confidence Intervals, Clearly Explained!!!
TLDRThis StatQuest episode delves into the concept of confidence intervals, a statistical tool often misunderstood. It introduces bootstrapping as a method to understand confidence intervals better. The video explains how to use bootstrapping with a sample of female mice weights to estimate the global mean. It then illustrates how to create a 95% confidence interval, which covers 95% of the bootstrapped means, and how it serves as a visual statistical test. The episode clarifies that a 99% confidence interval is wider and covers more of the means. It concludes with examples of using confidence intervals to detect statistically significant differences between sample means, emphasizing the importance of non-overlapping intervals for asserting significance.
Takeaways
- 📚 Confidence Intervals: The video discusses the concept of confidence intervals and their importance in statistics.
- 🧠 Misunderstandings: Many people misunderstand confidence intervals, often because they haven't learned about bootstrapping.
- 🔢 Calculation Methods: There are multiple ways to calculate confidence intervals, with bootstrapping being one of the methods explained in the video.
- 🐁 Mouse Weight Example: The script uses the example of weighing female mice to illustrate how bootstrapping and confidence intervals work.
- 🔼 Sample Mean: The sample mean is calculated from a subset of the population, in this case, 12 mice, and is not the mean of the entire population.
- 🔄 Bootstrapping: The process of bootstrapping involves randomly selecting samples with replacement from the original data to estimate the population mean.
- 📊 Multiple Means: By repeating the bootstrapping process many times, a distribution of means is created which can be used to establish confidence intervals.
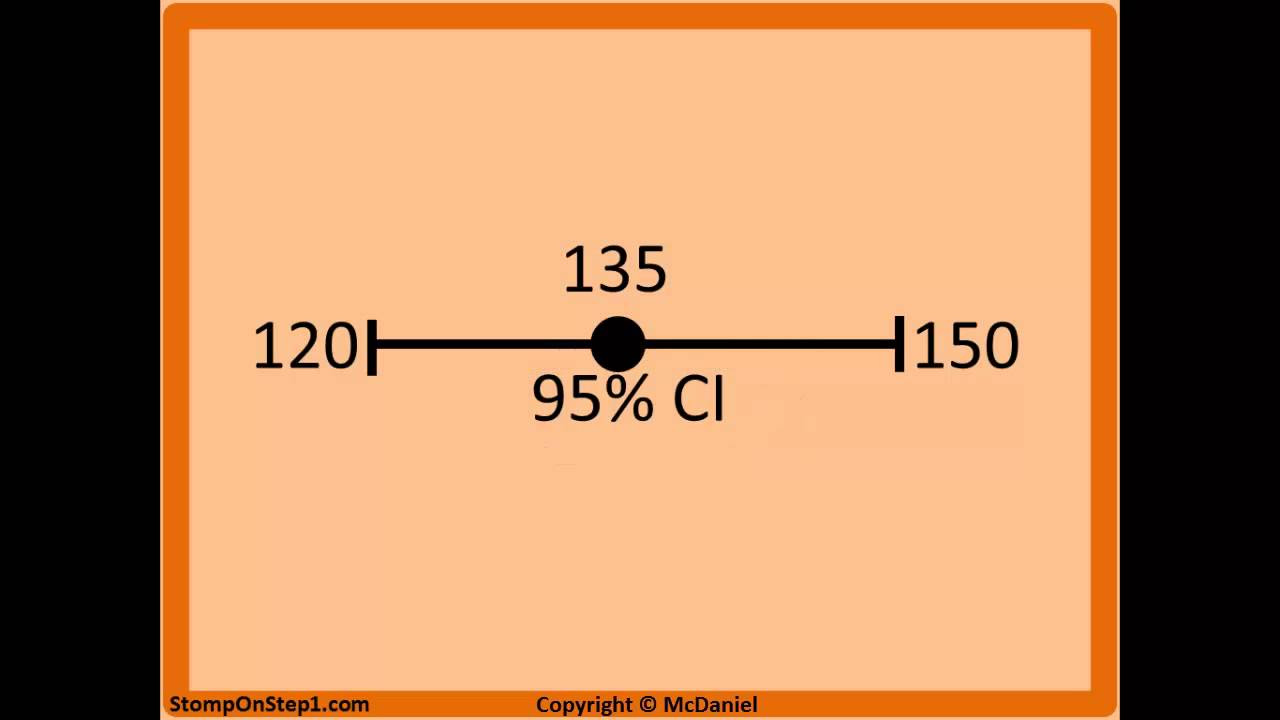
- 🔢 95% Confidence Interval: A common confidence interval is 95%, which covers 95% of the bootstrapped means and implies that the true mean is within this range with high probability.
- 📈 Visual Statistical Tests: Confidence intervals provide a visual method for statistical testing, allowing for quick assessments of significance.
- 🆚 Comparing Samples: The script shows how confidence intervals can be used to compare two samples, like the weights of female and male mice, to determine if there is a significant difference.
- ⚠️ Overlapping Intervals: A caveat is presented where overlapping confidence intervals do not necessarily mean no significant difference, and further testing may be required.
Q & A
What is the main topic of today's StatQuest video?
-The main topic of today's StatQuest video is confidence intervals and their understanding through the method of bootstrapping.
Why do many people misunderstand confidence intervals?
-Many people misunderstand confidence intervals because they often don't learn about bootstrapping first, which is a method that can make understanding confidence intervals easier.
What is bootstrapping in the context of statistics?
-Bootstrapping is a resampling technique used to estimate statistics on a population by sampling a dataset with replacement multiple times to create an empirical distribution of a statistic.
How does bootstrapping help in understanding confidence intervals?
-Bootstrapping helps in understanding confidence intervals by allowing us to simulate the sampling distribution of a statistic (like the mean) by resampling the original sample with replacement, which can then be used to construct confidence intervals.
What is the sample mean in the context of the mice example?
-The sample mean in the context of the mice example is the average weight of the 12 female mice that were weighed, which serves as an estimate for the mean weight of all female mice on the planet.
What is sampling with replacement in bootstrapping?
-Sampling with replacement in bootstrapping means that after selecting a sample from the original dataset, the same observation can be chosen again in subsequent samples, allowing for duplicates in the resampled datasets.
How many means are typically calculated in bootstrapping?
-In bootstrapping, a large number of means are calculated, sometimes more than 10,000, to create a robust sampling distribution.
What does a 95% confidence interval represent?
-A 95% confidence interval represents an interval that covers 95% of the bootstrapped means, indicating that we are 95% confident that the true mean lies within this interval.
Why are confidence intervals considered useful in statistics?
-Confidence intervals are useful because they provide a visual representation of the range in which the true population parameter is likely to fall, and they allow for statistical tests to be performed visually, with the p-value associated with values outside the interval.
How can a confidence interval be used to perform a visual statistical test?
-A confidence interval can be used to perform a visual statistical test by comparing the interval to a value of interest. If the value falls outside the interval, it suggests that the true mean is significantly different from that value with a p-value less than 0.05.
What does it mean when confidence intervals of two samples do not overlap?
-When confidence intervals of two samples do not overlap, it suggests that there is a statistically significant difference between the means of the two samples, indicating that the p-value is less than 0.05.
What is the caveat when using confidence intervals to determine if two means are significantly different?
-The caveat is that even if the confidence intervals overlap, there can still be a significant difference between the means. In such cases, a t-test or another statistical test would be necessary to determine significance.
Outlines
📊 Introduction to Confidence Intervals and Bootstrapping
The video begins with an introduction to confidence intervals, a statistical concept that is often misunderstood. The presenter suggests that understanding bootstrapping can clarify the concept of confidence intervals. Bootstrapping is a resampling technique used to estimate statistics on a dataset by sampling with replacement, which helps to infer the population parameters from a sample. The video uses the example of weighing a sample of female mice to explain how bootstrapping works and how it can be used to estimate the global mean of all female mice on the planet. The presenter also explains that confidence intervals, commonly seen as 95% intervals, represent a range that covers 95% of the means calculated through bootstrapping, providing a visual statistical test to determine significance.
🔍 Visual Statistical Tests with Confidence Intervals
This paragraph delves into the practical application of confidence intervals for visual statistical testing. The presenter illustrates how a 95% confidence interval can be used to determine the p-value and establish statistical significance. By comparing the interval to a hypothesized value, such as the true mean weight of female mice being less than 20, one can visually assess the likelihood of the hypothesis being incorrect. The video further explains how non-overlapping confidence intervals between two samples, like female and male mice, indicate a statistically significant difference with a p-value less than 0.05. However, if the confidence intervals overlap, it suggests that there is still a chance the means could be significantly different, and a t-test would be required to confirm. The video concludes by emphasizing the utility of visual statistical tests for quickly assessing significance without complex calculations.
Mindmap
Keywords
💡Confidence Intervals
💡Bootstrapping
💡Sample Mean
💡Sampling with Replacement
💡Statistical Significance
💡P-value
💡Visual Statistical Test
💡Population Mean
💡95% Confidence Interval
💡99% Confidence Interval
💡T-test
Highlights
Stat Quest is a video series by the genetics department at the University of North Carolina at Chapel Hill.
The episode focuses on explaining confidence intervals, a concept often misunderstood.
Bootstrapping is introduced as an easy way to understand confidence intervals.
Confidence intervals are calculated in various ways, with bootstrapping being just one method.
A refresher on bootstrapping is provided through the example of weighing female mice.
The sample mean is distinguished from the mean of the entire population.
Bootstrapping involves random selection with replacement to estimate global parameters.
The process of calculating the mean from a random sample is repeated many times in bootstrapping.
A visual representation of bootstrapped means helps in understanding confidence intervals.
A 95% confidence interval covers 95% of the bootstrapped means.
A 99% confidence interval is wider than a 95% interval, covering more of the calculated means.
Confidence intervals serve as a visual statistical test indicating the likelihood of certain outcomes.
The p-value of outcomes outside the confidence interval is less than 0.05, indicating significance.
An example demonstrates calculating the p-value for the true mean of female mice being less than 20.
Visual statistical tests can compare two samples, like female and male mice, for significant differences.
Non-overlapping confidence intervals between two samples indicate a significant difference.
Overlapping confidence intervals do not guarantee no significant difference, necessitating further tests.
Stat Quest aims to provide clear explanations of statistical concepts for better understanding.
Transcripts
Browse More Related Video

Confidence Interval [Simply explained]

How To Find The Z Score, Confidence Interval, and Margin of Error for a Population Mean

Confidence Intervals: Crash Course Statistics #20

What is a Confidence Interval? | Puppet Master of Statistics
Confidence Interval Interpretation. 95% Confidence Interval 90% 99%

Understanding Confidence Intervals: Statistics Help
5.0 / 5 (0 votes)
Thanks for rating: