Power & Effect Size
TLDRThis video delves into the concepts of statistical power and effect size, crucial for detecting relationships or differences in data. Power, defined as one minus beta, is the ability to find significance if it exists, with a common threshold of 0.8. The video explains that power is influenced by alpha levels, sample size, effect size, and the type of statistical test. Effect size measures the strength of a phenomenon, with Cohen's D being a key metric. The video also covers how increasing sample size or effect size can improve power, and introduces tools like G*Power for estimating sample size to ensure adequate power for statistical significance.
Takeaways
- 🔍 Power in statistical testing is the ability to detect a relationship or difference if it exists in the population.
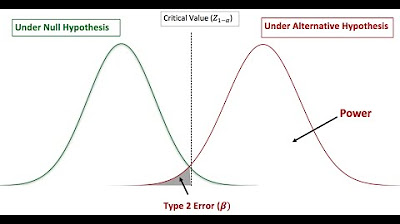
- 📉 Power is related to Type I and Type II errors, and it is the probability of rejecting a null hypothesis when it is false.
- 📊 Jacob Cohen is considered the father of power analysis, and power is calculated as one minus beta.
- 💪 Acceptable power levels are typically considered to be 0.8, but 0.7 is often adequate, especially in fields like education.
- 🔧 Power analysis is usually performed a priori, before a study begins, to ensure that the study has enough power to detect significance.
- 🚫 Post-hoc power analysis can be controversial and may be seen as a waste of time, as it does not provide useful information for the current study.
- 📉 Effect size measures the strength of a phenomenon or the difference between groups and is crucial in determining the power of a test.
- 📈 Cohen's D is a common measure of effect size used in T-tests, with thresholds of 0.2 for small, 0.5 for medium, and 0.8 for large effects.
- 🔬 Effect size is discovered a priori through literature review or pilot studies to understand typical effect sizes in a given field.
- 👥 Increasing sample size is a straightforward way to improve power, as it reduces the probability of a Type II error.
- 🛠️ Other ways to improve power include relaxing the alpha level, using more robust statistical tests, and increasing the reliability of the measures.
Q & A
What is the definition of power in the context of statistical testing?
-In the context of statistical testing, power is the ability of a test to detect a relationship or difference. It is the probability of rejecting a null hypothesis when it is false and should be rejected.
Why is power analysis important in research studies?
-Power analysis is important because it helps ensure that a study has enough power to detect a significant effect if it exists. Without sufficient power, a study may fail to find a difference even if one is present, leading to incorrect conclusions.
What is the relationship between power and type I and type II errors?
-Power is related to type I and type II errors in that it helps determine the likelihood of making these errors. A type I error occurs when the null hypothesis is incorrectly rejected (a 'false positive'), while a type II error occurs when the null hypothesis is not rejected when it should be (a 'missed difference'). Power helps in minimizing the chance of a type II error.
Who is Jacob Cohen and why is he significant in the context of power analysis?
-Jacob Cohen is considered the father of power analysis. His work has significantly contributed to the understanding and application of power in statistical tests, particularly through his development of Cohen's d, a measure used in power analysis.
What is the acceptable power level for a study and why might it vary?
-Acceptable power is generally considered to be 0.8, meaning there is an 80% chance of detecting an effect if it exists. However, in some fields like education, where many factors can influence outcomes, a power level of 0.7 might be considered adequate to allow for more variability.
What is Cohen's d and how is it used in power analysis?
-Cohen's d is a measure of effect size used in power analysis, particularly for T-tests. It quantifies the standardized difference between two means, helping to determine the magnitude of an effect and thus the power needed to detect it.
Why is it recommended to perform power analysis before starting a study?
-Performing power analysis before starting a study helps to ensure that the study has an adequate sample size and design to detect a significant effect. Post-hoc power analysis can be controversial and may be seen as an attempt to justify a study's findings after the fact.
What factors influence the power of a statistical test?
-Factors influencing the power of a statistical test include alpha level (the level of confidence), sample size, effect size, the type of statistical test used, and the design of the study.
Can you explain the concept of effect size and why it is important?
-Effect size is a measure of the strength or magnitude of a phenomenon or difference between groups. It is important because it helps determine the practical significance of a finding, not just its statistical significance. A larger effect size requires fewer subjects to detect a significant result, while a smaller effect size requires more subjects.
How does the size of the effect influence the power of a test?
-The larger the effect size, the greater the power of the test to detect a significant difference. A large effect size means that the difference between groups is substantial, making it easier to detect with fewer subjects, thus increasing power.
What are some ways to improve the power of a statistical test?
-To improve the power of a statistical test, one can relax the alpha level, use a more powerful statistical test, increase the reliability of the measure, use a one-tailed test instead of a two-tailed test, or most effectively, increase the sample size.
Outlines
🔍 Understanding Statistical Power and Effect Size
This paragraph introduces the concept of statistical power, which is the ability of a test to detect a relationship or difference when it exists. It discusses the relationship between power and type one and type two errors, emphasizing the importance of rejecting the null hypothesis correctly. The paragraph also introduces Jacob Cohen and the concept of power as one minus beta, with acceptable power levels typically being around 0.8. The speaker explains that power analysis should ideally be conducted a priori, before the study begins, to ensure that the study has enough power to detect significance. The influence of factors such as alpha level, sample size, effect size, and the type of statistical test on power is also discussed.
📊 The Role of Effect Size in Statistical Analysis
This paragraph delves into the concept of effect size, which measures the strength or magnitude of a phenomenon or difference between groups. It explains how effect size is crucial for understanding the significance of findings beyond mere statistical significance. The speaker discusses how effect size is related to the power of a test, with larger effect sizes requiring fewer subjects to detect a significant result. The paragraph also covers different ways to measure effect size, such as Cohen's D in T-tests and eta squared in ANOVA, and provides thresholds for small, medium, and large effect sizes. The importance of knowing the typical effect sizes in a field before conducting a study is highlighted, as well as the potential for conducting pilot studies to estimate effect size.
📈 Enhancing Power in Statistical Studies
The final paragraph focuses on strategies to improve the power of a statistical study. It suggests methods such as relaxing the alpha level, using more robust statistical tests, increasing sample size, and enhancing the sensitivity of the design or analysis. The speaker mentions the use of tables and computer programs like G*Power to estimate sample size and ensure adequate power. The paragraph also discusses the trade-offs and risks associated with certain strategies, such as using a one-tailed test, and emphasizes the importance of having a well-powered study to effectively detect meaningful differences or relationships.
Mindmap
Keywords
💡Power
💡Type I and Type II Errors
💡Cohen's D
💡Effect Size
💡Sample Size
💡Alpha Level
💡Null Hypothesis
💡Statistical Test
💡Power Analysis
💡Significance
Highlights
Power is the ability of a statistical test to detect a relationship or difference.
Power is linked to Type I and Type II errors and the decision based on P value.
Probability of rejecting a null hypothesis when it is false is the definition of power.
Cohen's D is a measure of effect size and is foundational in power analysis.
Acceptable power levels are typically 0.8, but 0.7 is often adequate in education.
Power analysis is usually conducted a priori, before a study begins.
Post-hoc power analysis can be controversial and seen as a waste of time.
Effect size measures the strength of a phenomenon or the difference between groups.
Effect size is crucial for determining the significance of differences in hypotheses testing.
Cohen's D is used in T-tests to measure the difference between two means.
Effect sizes are categorized as small, medium, or large, with specific numerical ranges.
A large effect size requires fewer subjects to find a significant result.
Increasing sample size is a straightforward way to improve power.
Relaxing Alpha levels, using parametric statistics, and increasing measure reliability can also improve power.
G*Power is a computer program that helps estimate sample size for adequate power.
Effect size is discovered a priori through literature review or pilot studies.
Variance within each distribution affects power and the ability to detect differences.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: