(Extra) Formal use of limit formula [IB Maths AI SL/HL]
TLDRThe video script provides an in-depth explanation of the concept of a derivative in calculus. It begins with a discussion on the importance of understanding limits, particularly for students taking the higher level (HL) math course, though it's noted that standard level (SL) students can also benefit from this foundational knowledge. The presenter uses the example of the function y = x^2 to illustrate the process of finding a derivative. By introducing a second point on the graph and gradually reducing the distance between the two points (represented by 'h'), the presenter shows how the gradient of the line connecting these points approaches the derivative. The formal definition of a derivative is presented as the limit of (f(x+h) - f(x)) / h as h approaches 0. The script then demonstrates how to calculate the derivative of x^2 by hand, leading to the result of 2x, and highlights a shortcut method for finding derivatives quickly. The presenter also mentions the utility of calculators for such calculations. The video concludes by emphasizing the importance of understanding the formal process of derivatives, even if in practice, students often rely on shortcuts and technology.
Takeaways
- 📚 The concept of a limit is fundamental to understanding derivatives, even for those taking the Math SL course, as it provides a formal definition of how derivatives are calculated.
- 🔍 The derivative represents the gradient of a tangent line to a curve at a specific point, which is found by 'squeezing' two points together until they coincide.
- 📈 The formal definition of a derivative involves taking the limit as the change in x (h) approaches zero, resulting in the gradient of the function at a given point.
- 🤔 The process of finding a derivative by hand involves creating a second point on the graph, calculating the change in y (delta y) and the change in x (delta x), and then finding the limit as h approaches zero.
- 🎓 For the function f(x) = x^2, the derivative at x = 1 can be found by substituting x with 1 and evaluating the limit as h approaches zero.
- 👉 The derivative of f(x) = x^2 is found to be f'(x) = 2x, which is a general rule that can be applied quickly without the need for the formal limit process.
- 🧮 Using a calculator can simplify the process of finding derivatives, as demonstrated by the script where the derivative at x = 1 is found to be 2.
- 📐 The gradient of a tangent line at a specific point on a graph can also be visualized and calculated by drawing the line and measuring its slope.
- 🚀 There's a trick for quickly finding the derivative of a function like f(x) = x^n, which involves bringing down the coefficient (n), reducing the exponent by one, and multiplying.
- 📝 The formal method of finding derivatives by using limits is an important concept to understand, but in practice, shortcuts and calculators can be used for efficiency.
- 🔁 The process of finding derivatives involves an iterative approach of substitution, simplification, and evaluation of limits, which ultimately leads to the gradient of the function at a specific point.
Q & A
What is the concept of a limit in calculus?
-The concept of a limit in calculus is a fundamental idea that describes the value that a function or sequence 'approaches' as the input (or index) approaches some value. In the context of derivatives, it is used to find the instantaneous rate of change of a function at a particular point by squeezing two points together until they are infinitely close.
Why is it necessary to use two points to find the derivative of a function?
-Two points are necessary to find the derivative because the derivative represents the gradient (slope) of a line, and a line is defined by two distinct points. By taking the limit as the distance between these two points approaches zero, we find the instantaneous rate of change at a single point.
What does the term 'gradient' refer to in the context of derivatives?
-In the context of derivatives, the term 'gradient' refers to the slope of the tangent line to a curve at a given point. It is the rate of change of the function at that point and is found by taking the limit of the average rate of change as the interval between two points approaches zero.
What is the formal definition of the derivative of a function at a point x?
-The formal definition of the derivative of a function f at a point x, denoted as f'(x) or df/dx, is the limit as h approaches 0 of the difference quotient [f(x + h) - f(x)] / h.
How does the concept of 'squeezing' points together relate to finding the derivative?
-The concept of 'squeezing' points together is a visual way to describe the process of finding the derivative. By bringing a second point infinitely close to the first point (the point of interest), the gradient of the line connecting these two points approaches the gradient of the tangent line at the first point, which is the derivative.
What is the purpose of introducing a second point, x + h, in the process of finding the derivative?
-The purpose of introducing a second point, x + h, is to create a pair of points that can be used to calculate the gradient of a line, which approximates the tangent line to the graph of the function at the point x. As h approaches zero, this approximation becomes more accurate, eventually giving the exact derivative at x.
What is the significance of the term 'h' in the derivative formula?
-The term 'h' in the derivative formula represents a small change in the x-value of the function. It is used to create a second point that, along with the original point, allows us to calculate the average rate of change between the two points. As h approaches zero, this rate of change converges to the instantaneous rate of change, which is the derivative.
How does the process of finding the derivative by hand compare to using a calculator?
-Finding the derivative by hand involves a more detailed and step-by-step approach, using the limit definition and algebraic manipulation to simplify and solve for the derivative. Using a calculator, on the other hand, provides a quick and direct way to find the derivative at a specific point without going through the entire limit process.
What is the advantage of learning the formal method of finding derivatives, even if it's not used frequently?
-Learning the formal method of finding derivatives helps in understanding the underlying concept and the mathematical reasoning behind the process. It provides a solid foundation for grasping more advanced calculus concepts and techniques, even though in practice, simpler methods or tools like calculators are often used for efficiency.
What is the shortcut method for finding the derivative of a function f(x) = x^n?
-The shortcut method for finding the derivative of a function f(x) = x^n is to use the power rule, which states that the derivative f'(x) = n * x^(n-1). For the specific case of f(x) = x^2, the derivative is f'(x) = 2x.
What does the term 'dy/dx' represent in calculus?
-The term 'dy/dx' represents the derivative of y with respect to x. It is a notation for the rate at which the dependent variable y changes with respect to the independent variable x. In the context of the limit definition, it is the result of taking the limit as the change in x (h) approaches zero of the difference quotient [f(x + h) - f(x)] / h.
How does the process of finding the derivative at a specific point, such as x = 1, differ from finding the derivative in general?
-When finding the derivative at a specific point, such as x = 1, you substitute that value into the derivative formula to find the instantaneous rate of change at that point. In contrast, finding the derivative in general involves not substituting a specific value for x but rather simplifying the expression to find the derivative function, which gives the rate of change for all points in the domain of the original function.
Outlines
📚 Introduction to Limits and Derivatives
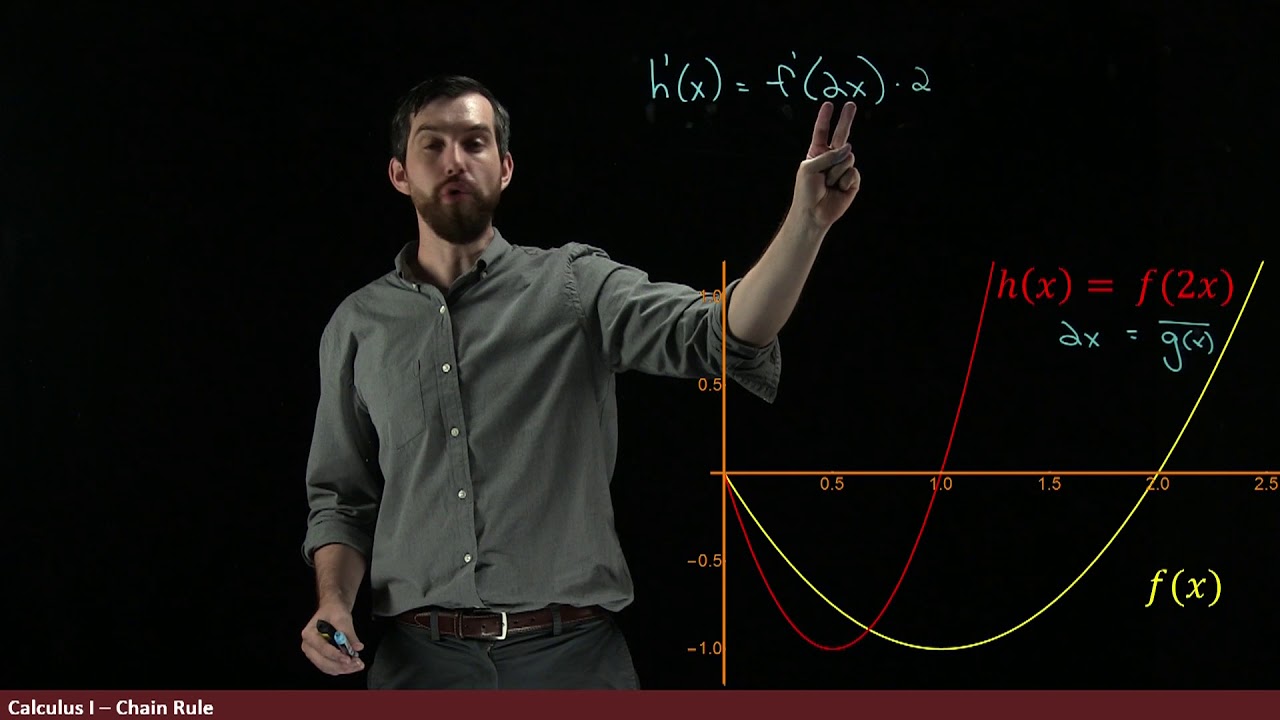
The first paragraph introduces the concept of limits in the context of calculus, specifically for those taking the higher-level math course. The speaker explains that while it's not required for the standard level, it's still beneficial to understand. The paragraph delves into the formal definition of a limit by using the example of the equation y=x^2 at x=1. It discusses the challenge of finding the gradient of a single point on a graph by introducing a second point and the concept of 'squeezing' these points together to find the derivative. The formal formula for a derivative is introduced as the limit of (f(x+h) - f(x)) / h as h approaches 0, where f(x) represents a general function.
📐 Derivative Calculation and Tangent Approximation
The second paragraph continues the discussion on derivatives, illustrating how to calculate them both graphically and using a calculator. It demonstrates finding the derivative at a specific point on a graph, such as x=1 for the function y=x^2, by drawing a tangent line or using the calculator's derivative function. The speaker then shows how to calculate the derivative by hand using the limit definition, substituting f(x) with x^2 and simplifying the expression as h approaches 0, which results in the derivative of 2 at x=1. The paragraph concludes by highlighting the practicality of using a calculator for such calculations.
🔍 Simplifying Derivative Calculation with Power Rule
The third paragraph simplifies the process of finding derivatives by introducing a trick known as the power rule. It explains that for a function f(x) = x^n, the derivative f'(x) is found by bringing down the exponent as the coefficient and reducing the exponent by one. Using the example of f(x) = x^2, the speaker demonstrates that the derivative is 2x, where the '2' comes from the exponent and 'x' is the base with the exponent reduced by one. This trick allows for quick mental calculation of derivatives without the need for the formal limit process, making it a more efficient method for students to use in practice.
Mindmap
Keywords
💡Limit
💡Derivative
💡Gradient
💡Function
💡Tangent Line
💡Delta (Δ)
💡Slope
💡Calculator
💡Mathematical Trick
💡Power Rule
Highlights
The concept of a limit is introduced as a fundamental aspect of understanding derivatives, even for those studying the Math SL course.
The formal definition of a limit is demonstrated through the equation y = x^2 at x = 1.
Derivatives are explained as the gradient of a line, which traditionally joins two points.
The process of 'squeezing' two points together to find the derivative is illustrated.
Generalization of the concept is shown by replacing x^2 with a generic function f(x).
Introduction of a second point x + h to help in the calculation of the derivative.
The official formula for a derivative is derived from the concept of delta y over delta x.
The limit as h approaches 0 of (f(x + h) - f(x))/h is shown to be the formal method to calculate the derivative.
A calculator can be used to find the derivative, demonstrated by finding the derivative at x = 1 for y = x^2.
The manual calculation of the derivative for f(x) = x^2 is shown step by step.
The use of the limit process to avoid division by zero is explained.
The final result of the derivative of f(x) = x^2 at x = 1 is found to be 2.
An alternative quick method for finding derivatives, known as 'the power rule', is introduced.
The power rule simplifies the process to 2x for f(x) = x^2, making it possible to calculate derivatives mentally.
The importance of understanding the formal method of derivatives, even if a shortcut or calculator is available.
The transcript emphasizes the value of knowing the underlying theory behind mathematical operations, despite the availability of tools that simplify the process.
The demonstration of both manual and calculator methods for finding derivatives provides a comprehensive understanding of the topic.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: