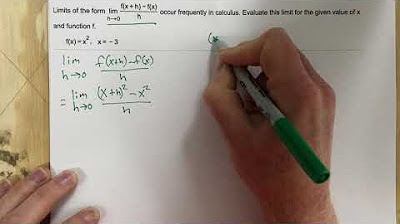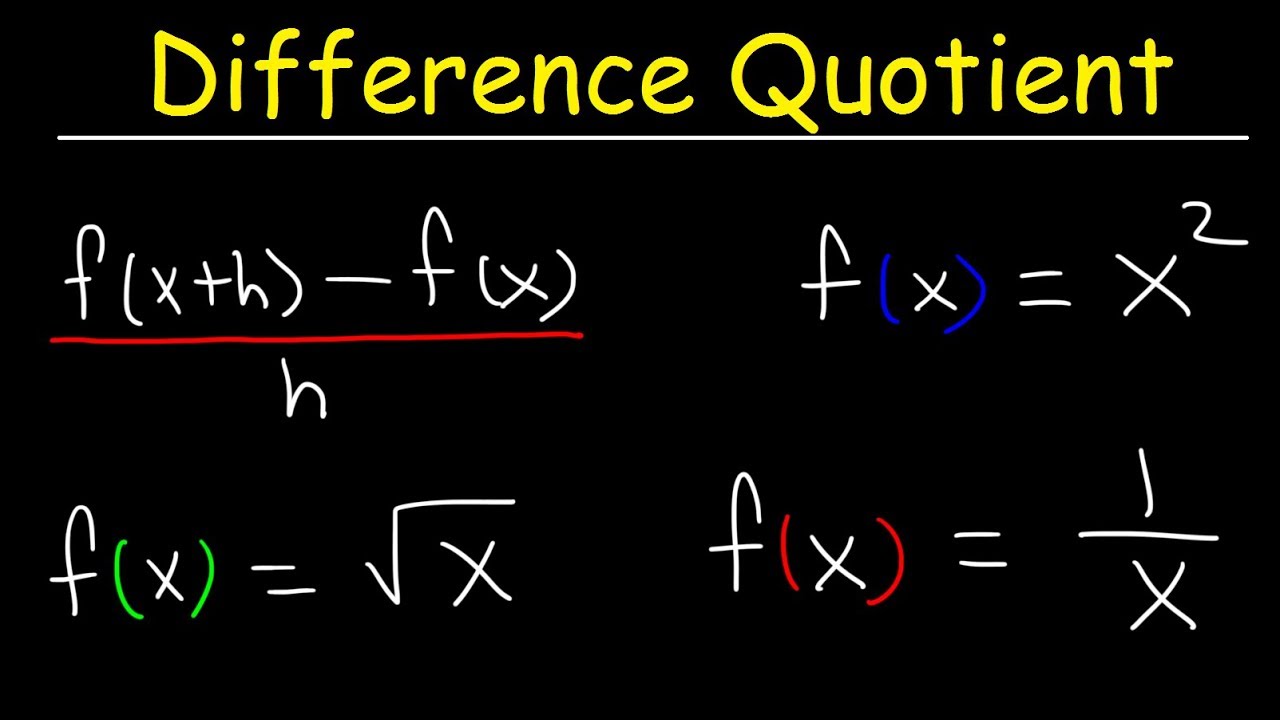More Difference Quotient Examples
TLDRThe video script provides a detailed explanation on how to calculate the difference quotient, which is a method for finding the slope of a tangent line to a curve at a given point. The process involves substituting 'x + h' for 'x' in a given function, simplifying the expression, and then taking the limit as 'h' approaches zero. The script illustrates this with two examples: the first with the function '1/(x + h - 5)' and the second with '(x + h)^3 + 2'. It emphasizes the importance of not substituting zero for 'h' too early to avoid an indeterminate form. The final results for the difference quotients are '-1/(x - 5) * (x - 5)^2' for the first example and '3x^2' for the second. The script concludes by noting that the difference quotient is a general formula for determining the rate of change at any point on a graph.
Takeaways
- 📐 The script discusses the concept of the difference quotient, which is a general formula for finding the slope or rate of change at any point along a graph.
- 🔍 When substituting into a function, replace every instance of 'x' with '(x + H)' to find the difference quotient.
- ❗ Avoid substituting H with zero prematurely to prevent an indeterminate form (0/0), which does not provide a conclusive result.
- 🧮 Multiply by the common denominator to simplify the expression before substituting zero for H, which helps to avoid indeterminate forms.
- 📉 The difference quotient is used to find the slope of the tangent line at a specific point on a graph, representing the instantaneous rate of change at that point.
- 📌 Remember to treat subtraction as subtracting the entire group, especially when dealing with parentheses, to ensure accuracy in the calculation.
- 📚 Pascal's triangle can be a useful tool for quickly expanding terms with powers, such as in the example of (x + H)^3.
- 🔢 After expanding and simplifying the expression, factor out common terms like 'H' to further simplify the difference quotient.
- 🎯 The final step is to take the limit as H approaches zero, which gives the derivative of the function at the point x.
- 📍 The slope of the tangent line can vary depending on the x-value, as demonstrated by the examples where x equals 4 and x equals 10.
- 🔗 Additional resources are provided in the video description for further understanding of the difference quotient and related topics.
Q & A
What is the purpose of the difference quotient in calculus?
-The difference quotient is a general formula used to find the slope of a tangent line at any point on a graph, representing the rate of change at that point.
Why is it important not to substitute zero into H too early in the difference quotient calculation?
-Substituting zero into H too early can lead to an indeterminate form of 0/0, which does not provide a conclusive result and can mislead the calculation.
How does the process of finding the difference quotient help in understanding the rate of change of a function?
-The process of finding the difference quotient involves manipulating the function to isolate the variable H, which, when taking the limit as H approaches zero, provides the instantaneous rate of change at a specific point on the graph.
What is the role of Pascal's triangle in expanding expressions like (x + H)^n?
-Pascal's triangle provides the binomial coefficients for expanding expressions of the form (x + H)^n, making it a quick and efficient method to find the expanded form without manually distributing each term.
Why is it necessary to keep the numerator and denominator equivalent when performing operations on fractions?
-Maintaining equivalence ensures that the value of the fraction does not change during the manipulation process, which is crucial for preserving the integrity of the mathematical expression.
How does the factoring out of H simplify the difference quotient formula?
-Factoring out H from terms in the numerator and denominator allows for cancellation, simplifying the expression and making it easier to take the limit as H approaches zero.
What is the final form of the difference quotient for the function f(x) = x^2 - 5?
-The final form of the difference quotient for the function f(x) = x^2 - 5 is -1/(x + H - 5) * (x - 5), which simplifies to -1/x - 5 after substituting zero for H.
For the function f(x) = x^3 + 2, what is the simplified form of the difference quotient?
-The simplified form of the difference quotient for the function f(x) = x^3 + 2 is 3x^2, after taking the limit as H approaches zero.
How does the process of distributing and simplifying terms in the numerator and denominator help avoid mistakes in the calculation of the difference quotient?
-Distributing and simplifying terms systematically ensures that each part of the expression is correctly accounted for, reducing the chance of errors such as forgetting to include parentheses or incorrectly combining terms.
What is the significance of the difference quotient in determining the slope of the tangent line at a specific point on a graph?
-The difference quotient, when evaluated at a specific point, provides the slope of the tangent line at that point, which is a measure of the instantaneous rate of change or incline of the graph at that location.
How does the process of substituting x + H for x in the function relate to the concept of finding the rate of change?
-Substituting x + H for x introduces a small change in the input of the function, which, when used in the difference quotient formula, allows for the calculation of the rate of change or slope at the point x as H approaches zero.
What is the role of the common denominator in simplifying the difference quotient before taking the limit as H approaches zero?
-Multiplying by the common denominator allows for the combination of terms in the numerator and denominator, which can lead to cancellations and simplification of the expression, making it easier to evaluate the limit as H approaches zero.
Outlines
🔢 Deriving the Difference Quotient
This paragraph explains the process of finding the derivative of a function using the difference quotient. The speaker begins by substituting x with x + H in the function and then simplifies the expression before taking the limit as H approaches zero. The goal is to avoid an indeterminate form (0/0) by simplifying before substituting zero for H. The process involves multiplying by the common denominator, distributing the terms, and canceling out common factors. The final result is a simplified difference quotient that can be used to find the slope of the tangent line at any point on the graph of the original function.
📈 Simplifying the Difference Quotient for a Cubic Function
In this paragraph, the focus is on simplifying the difference quotient for a cubic function, f(x) = x^3 + 2. The speaker demonstrates how to expand (x + H)^3 using Pascal's triangle, which is a more efficient method than foiling. After expanding and simplifying the expression, the H terms are factored out, and the limit as H approaches zero is taken. The resulting difference quotient is 3x^2, which represents the slope of the tangent line at any point on the graph of the function. The paragraph concludes with an example of how to use the difference quotient to find the slope at a specific point, x = 1, resulting in a slope of 3.
Mindmap
Keywords
💡Input
💡Function
💡Difference Quotient
💡Limit
💡Indeterminate Form
💡Common Denominator
💡Factoring
💡Pascal's Triangle
💡Slope of the Tangent Line
💡Instantaneous Rate of Change
💡Cubing
Highlights
The input to a function is represented by whatever is inside the parentheses, which replaces x in the function.
The difference quotient is a general formula for finding the slope or rate of change at any point along a graph.
To avoid an indeterminate form, simplify the expression before substituting zero in for H.
Multiply by the common denominator to simplify the difference quotient expression.
Distribute the common denominator to both the numerator and denominator to keep the expression equivalent.
Cancel out like terms in the numerator and denominator to simplify the expression further.
Factor out common factors like H from the numerator and denominator to simplify the expression.
The difference quotient can be used to find the slope of the tangent line at any point on the graph.
Substitute x + H for x in the function to find the difference quotient.
Use Pascal's triangle to expand (x + H)^3 for a faster calculation.
Simplify the expanded expression by canceling out like terms.
Factor out H from each term in the numerator to further simplify the expression.
Evaluate the limit as H approaches zero to find the simplified difference quotient.
The difference quotient represents the instantaneous rate of change at a specific point on the graph.
The slope of the tangent line at a specific point can be found using the difference quotient.
The graph is not rising at a continuous rate, so the slope will vary at different points.
The process of finding the difference quotient involves substituting, simplifying, and evaluating limits.
Understanding the difference quotient is key to finding the slope of a tangent line and the rate of change at any point on a graph.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: