Velocity and speed: Motion in One Dimension

Miss Martins Maths and Science
10 Sept 202314:11
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the fundamental differences between speed and velocity, two critical concepts in physics. Speed is defined as a scalar quantity that measures the total distance traveled over time, without considering direction, and is commonly measured in meters per second (m/s) or kilometers per hour (km/h). In contrast, velocity is a vector quantity that includes both magnitude and direction, calculated as the displacement (change in position) over time. The script clarifies that while the units for speed and velocity are the same, their meanings differ significantly due to the inclusion of direction in velocity calculations. The video also provides a practical example of calculating both speed and velocity for a person running a certain distance in opposite directions, emphasizing the importance of understanding the directional aspect of velocity. Additionally, it offers a conversion method between m/s and km/h, and encourages viewers to explore more physics concepts through provided links.

Takeaways
  • 📏 **Speed vs. Velocity**: Speed is a scalar quantity with only magnitude, while velocity is a vector quantity with both magnitude and direction.
  • 🔄 **Unit of Measure**: Both speed and velocity are measured in meters per second (m/s), which can sometimes cause confusion between the two concepts.
  • 🧭 **Directional Significance**: Velocity includes direction, which is why it's often specified with terms like 'to the right' or 'east', whereas speed does not.
  • 📚 **Equations of Motion**: The equations of motion used in physics can be applied to calculate both speed and velocity, with the key difference being the inclusion of direction for velocity.
  • 📐 **Calculating Speed**: Speed is calculated as the total distance traveled divided by the total time taken, without considering direction.
  • 📍 **Calculating Velocity**: Velocity is calculated using displacement (change in position) divided by time, which accounts for direction.
  • 🔢 **Conversion**: The conversion between kilometers per hour (km/h) and meters per second (m/s) involves multiplying by 3.6 to convert m/s to km/h and dividing by 3.6 for the reverse.
  • 🌐 **Units of Speed and Velocity**: While m/s is the SI unit, other units like km/h are commonly used, especially for vehicles.
  • 📈 **Distance vs. Displacement**: Distance is the total path length traveled, whereas displacement is the straight-line change in position from start to finish.
  • ⏱️ **Time Consideration**: The time taken for an object to move is a common factor in calculating both speed and velocity.
  • 🏃 **Example Calculation**: In the given example, Simon's average speed is calculated using the total distance run, while his average velocity considers the final position relative to the start.
Q & A

  • What is the primary difference between speed and velocity?

    -The primary difference between speed and velocity is that speed is a scalar quantity, meaning it has only magnitude without direction, while velocity is a vector quantity, which means it has both magnitude and direction.

  • Why can the same unit, such as meters per second, be used for both speed and velocity?

    -The same unit can be used for both speed and velocity because they are related physical quantities, and the unit represents the magnitude of motion. However, the context in which the unit is used can indicate whether speed or velocity is being referred to, especially when a direction is mentioned.

  • How can the equations of motion be used to calculate speed?

    -The equations of motion, which include variables for acceleration and time, can be used to calculate speed because speed, like velocity, is related to how an object's motion changes over time. The key difference is that the result for speed will not include a direction component.

  • What is the formula for calculating average speed?

    -The formula for calculating average speed is total distance traveled divided by total time taken. It is represented as speed (S) = distance (d) / time (t).

  • How is average velocity different from average speed?

    -Average velocity is the rate of change of position over time, which means it considers the change in position (displacement) and requires a direction. In contrast, average speed only considers the total distance traveled over time and does not require a direction.

  • What is the unit for speed and velocity in the International System of Units (SI)?

    -In the International System of Units (SI), the standard unit for both speed and velocity is meters per second (m/s).

  • How can one convert between kilometers per hour (km/h) and meters per second (m/s)?

    -To convert from kilometers per hour to meters per second, you divide by 3.6 (since 1 km = 1000 m and 1 hour = 3600 seconds). To convert from meters per second to kilometers per hour, you multiply by 3.6.

  • What is displacement in the context of physics?

    -Displacement is the change in position of an object and is a vector quantity. It is represented by the straight-line distance from the initial to the final position, with a specified direction.

  • Why is the calculation of speed different from the calculation of velocity in the example provided?

    -In the example, the calculation of speed involves adding the distances traveled in both directions (regardless of direction), while the calculation of velocity involves considering the initial and final positions (displacement), which takes into account the direction of travel.

  • How did the example illustrate the difference between distance and displacement?

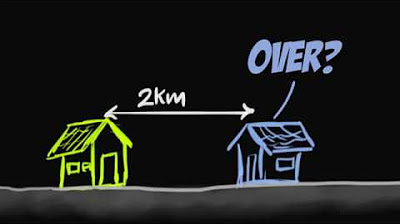
    -In the example, the total distance traveled by Simon was the sum of the distances in both directions (12 km), while the displacement was the straight-line distance from the starting point to the final position (2 km South), considering the direction of travel.

  • What is the final calculated average speed and velocity for Simon in the example?

    -The calculated average speed for Simon is 4.29 m/s, and the average velocity is 0.71 m/s to the South.

  • Why is it important to include the direction when calculating velocity but not when calculating speed?

    -Velocity is a vector quantity, so including direction is essential to fully describe the motion. Speed, on the other hand, is a scalar quantity and only describes the magnitude of motion without regard to direction, so it does not require a directional component.

Outlines
00:00
📏 Understanding Speed vs. Velocity

This paragraph explains the fundamental difference between speed and velocity. Speed is a scalar quantity that only has magnitude without direction, while velocity is a vector quantity that includes both magnitude and direction. Both are measured in meters per second (m/s), which can lead to confusion. However, context can clarify whether speed or velocity is being referred to, especially when a direction is mentioned. The paragraph also touches on the equations of motion used in physics education and how they can be applied to calculate both speed and velocity, despite their differences.

05:01
🔄 Converting Units of Speed and Velocity

The second paragraph delves into the conversion between different units of speed and velocity, specifically between meters per second and kilometers per hour. It explains the concept of 'per' as division and how to convert kilometers to meters and hours to seconds. The conversion factor between km/h and m/s is 3.6, with the process of dividing by 3.6 to go from km/h to m/s and multiplying by 3.6 for the reverse conversion. The paragraph also provides an example calculation of speed using the formula distance divided by time, emphasizing that speed is a scalar and does not require a direction.

10:03
🏃‍♂️ Calculating Speed and Velocity with an Example

The final paragraph illustrates the calculation of both speed and velocity using a practical example. It describes Simon's run, where he runs 5 km North and then 7 km South, and the time taken for this run is 2800 seconds. The average speed is calculated using the total distance traveled, which is a scalar quantity, resulting in 4.29 m/s. To find the average velocity, the paragraph explains the concept of displacement, which is the change in position and includes direction. Simon's displacement is calculated as 2000 meters South, leading to a velocity of 0.71 m/s South. The distinction between distance (for speed) and displacement (for velocity) is highlighted, along with the importance of direction in defining velocity.

Mindmap
Keywords
💡Speed
Speed is a scalar quantity that refers to 'the total distance traveled per total time'. It is a measure of how fast an object is moving, without considering the direction of movement. In the video, speed is calculated using the formula speed = distance/time, and it is given in units like meters per second or kilometers per hour. An example from the script is calculating the speed of a runner, which is the total distance covered divided by the time taken, without regard to the direction of travel.
💡Velocity
Velocity is a vector quantity that includes both magnitude and direction, defined as 'the rate of change of position'. Unlike speed, velocity takes into account not just how fast an object is moving but also the direction of that movement. In the context of the video, when Simon runs north and then south, his velocity is calculated using displacement (change in position) divided by time, resulting in a vector pointing in the direction of the net movement.
💡Scalar Quantity
A scalar quantity is a simple number that has only magnitude and no direction. It is one of the fundamental properties that distinguish speed from velocity. In the video, it is mentioned that speed is a scalar because it does not have a direction associated with it, only the magnitude of how much distance an object covers in a given time frame.
💡Vector Quantity
A vector quantity is a quantity that has both magnitude and direction, making it a more complex property than a scalar. It is a key concept in the video when differentiating between speed and velocity. Velocity is described as a vector because it includes information about the direction of movement, which is essential for understanding motion in physics.
💡Meters per Second (m/s)
Meters per second is the standard unit of speed and velocity in the International System of Units (SI). It is used to express both speed and velocity in the video, although it is important to note that while both use this unit, they represent different physical quantities. The video clarifies that speed in m/s is a scalar and does not include direction, whereas velocity in m/s is a vector and includes direction.
💡Kilometers per Hour (km/h)
Kilometers per hour is another common unit for expressing both speed and velocity, particularly in contexts like road travel. The video provides a conversion method between km/h and m/s, emphasizing that while the units can be used for both quantities, the physical concepts they represent are distinct. For example, a car's speed might be given in km/h for practical reasons, but the underlying physics would still consider it a scalar quantity.
💡Displacement
Displacement is the change in position of an object and is represented by a vector quantity. It is a critical concept in calculating velocity. In the video, displacement is used to determine the net change in position after Simon's run, which is different from the total path length (distance) he covered. Displacement is calculated as the straight-line distance from the starting point to the ending point with a consideration of direction.
💡Distance
Distance is the total path length traveled by an object and is a scalar quantity. It is used in the calculation of speed but not velocity, as it does not consider direction. In the video, distance is the sum of the lengths of all the paths taken by an object, regardless of the direction of travel. For Simon's run, the total distance is the sum of the distances he ran north and south.
💡Equations of Motion
Equations of motion are mathematical formulas used to describe the motion of an object. They relate variables such as acceleration, time, and velocity. In the video, these equations are mentioned in the context of calculating speed and velocity, emphasizing that while they are typically used for velocity, they can also be applied to calculate speed by ignoring the direction component.
💡Conversion
Conversion refers to the process of changing from one unit of measurement to another. In the context of the video, conversion is shown between km/h and m/s, which is essential for understanding how to express speed and velocity in different units. The video provides a shortcut for converting between these units, which is useful for solving physics problems and understanding real-world applications.
💡Average Speed
Average speed is calculated as the total distance traveled divided by the total time taken. It is a scalar quantity and does not include direction. In the video, average speed is used to describe the overall rate at which an object, such as a runner, moves over a period of time without considering the path taken or the direction of motion.
💡Average Velocity
Average velocity is the total displacement divided by the total time taken. It is a vector quantity and includes direction. The video explains that average velocity is different from average speed because it considers the direction of movement. For Simon's example, his average velocity is calculated based on his displacement from the starting point to the ending point, taking into account the direction he ran.
Highlights

Speed is a scalar quantity, having only magnitude without direction.

Velocity is a vector quantity, which includes both magnitude and direction.

Speed and velocity share the same unit of measurement, meters per second (m/s).

Velocity can be specified with a direction, such as '5 meters per second to the right'.

Speed does not require a direction, whereas velocity does.

Equations of motion can be used to calculate both speed and velocity.

Average speed is defined as the total distance traveled per total time.

Average velocity is the rate of change of position with respect to time.

Velocity uses displacement (a vector quantity) divided by time, while speed uses distance (a scalar) divided by time.

Units for speed and velocity can vary, including kilometers per hour (km/h).

Conversion between m/s and km/h involves multiplying by 3.6 for km/h to m/s and dividing by 3.6 for m/s to km/h.

Example problem: Simon runs 5 km North and then 7 km South in 2800 seconds.

Calculating speed involves summing the distances traveled, resulting in 12 km or 12,000 meters.

Calculating velocity involves determining the displacement, which is the initial position to the final position, resulting in -2 km South or 2000 meters South.

Simon's average speed is 4.29 m/s, indicating the total distance traveled over time without direction.

Simon's average velocity is 0.71 m/s South, indicating the change in position over time with direction.

Understanding the difference between speed and velocity is crucial for solving physics problems involving motion.

Transcripts

Browse More Related Video

Distance vs. Displacement & Speed vs. Velocity | Kinematics Explained

Displacement and Velocity - How is it different from Distance and Speed? | Physics

What is Velocity? Physics

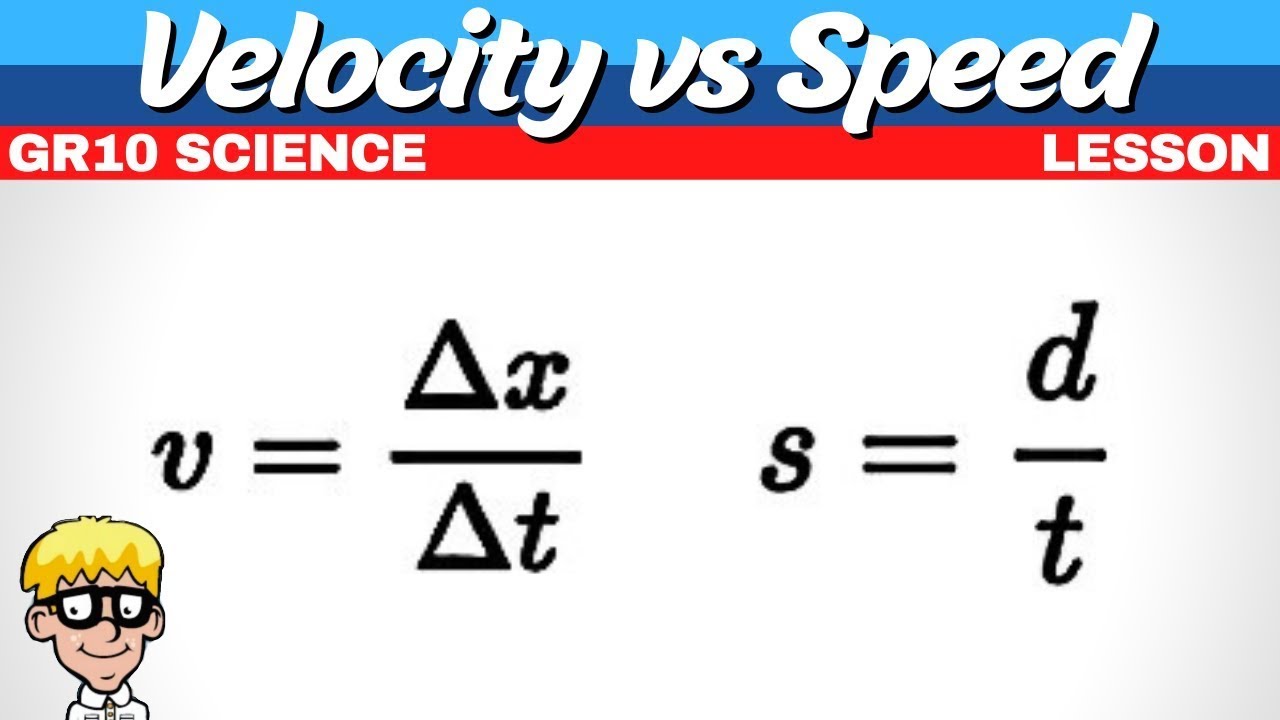
Velocity vs Speed Grade 10 Science

Average speed & velocity (with examples)

What is Velocity? - Full Concept of Velocity - Physics | Infinity Learn

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Speed vs VelocityPhysics ConceptsScalar VectorMotion AnalysisUnit ConversionMeters Per SecondKilometers Per HourDisplacementDistance CalculationEquations of MotionPhysics EducationScience Tutorial