Business Midterm Exam Review Solutions Part 2
TLDRThe video script is a comprehensive calculus review for an online midterm exam, focusing on business and social sciences applications. It covers a range of topics including finding derivatives, using implicit differentiation, analyzing functions for increasing and decreasing intervals, determining concavity, and applying the second derivative test for local extrema. The instructor also tackles related rates problems and optimization issues, such as maximizing the area of a rectangular storage facility with a given perimeter. The review is designed to prepare students for their midterm, emphasizing the importance of understanding calculus concepts and practicing problems. The instructor encourages students to graph functions using tools like Desmos for a better understanding and to reach out for any questions.
Takeaways
- 📚 The importance of attempting practice problems before watching solution videos to enhance learning through active problem-solving.
- 🔑 Derivatives can be found using the power rule, which is essential for calculus problems, as demonstrated in the video with the function f(x) = x + 1/x^2.
- 📈 Understanding the concept of implicit differentiation is crucial for solving calculus problems involving equations where y is implicitly a function of x.
- 📊 The process of finding intervals of increase and decrease of a function involves calculating the first derivative and analyzing its sign.
- 🔍 To determine concavity and inflection points, one must find the second derivative of a function and look for where it's positive (concave up) or negative (concave down).
- 🏗️ The second derivative test is a method used to find local extrema of a function by analyzing the concavity at critical points.
- 📌 The concept of absolute extrema on a closed interval requires checking both critical points and endpoints of the interval.
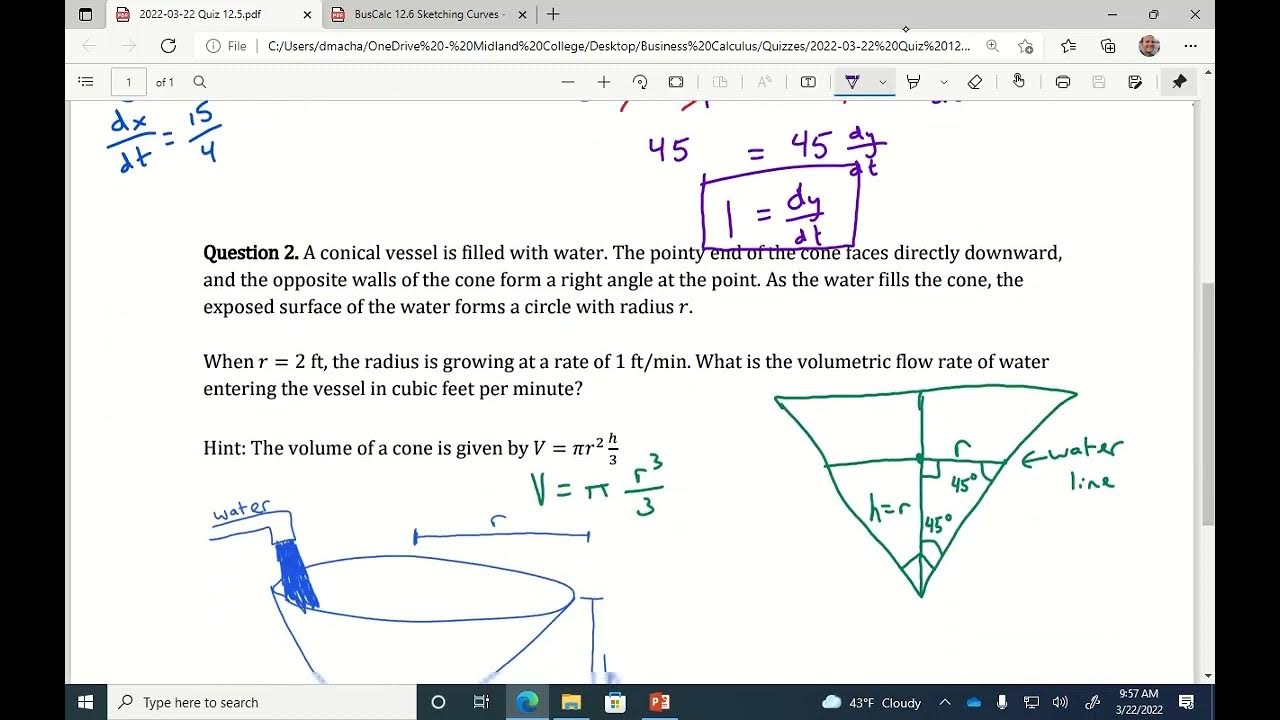
- 📐 Related rates problems, such as the ladder problem, involve using calculus to determine how quickly one quantity is changing in relation to another.
- 🧱 Optimization problems, like finding the dimensions of a fence for maximum area, can be solved using calculus by finding the maximum of an area function.
- ⚖️ The Pythagorean theorem is a fundamental tool used in various problems, including those involving right triangles and related rates.
- 📉 In optimization problems, it's important to consider the constraints, such as the total length of fencing available, and how they affect the variables in the problem.
Q & A
What is the main topic of the video script?
-The main topic of the video script is a review of calculus problems for a midterm exam, specifically focusing on derivatives, implicit differentiation, related rates, and optimization problems.
How does the instructor suggest students approach solving calculus problems before watching the video?
-The instructor suggests that students should try to solve the problems on their own before watching the video to enhance their learning experience.
What is the first problem discussed in the video, and what does it involve?
-The first problem involves finding the first and second derivatives of the function f(x) = (x + 1) / x^2. The instructor simplifies the function and then applies the derivative power rule to find the derivatives.
How does the instructor approach implicit differentiation in the second problem?
-The instructor uses implicit differentiation by taking the derivative of every term in the given equations with respect to x, applying the product rule and chain rule as necessary, and then solving for dy/dx.
What is the concept of critical points in calculus, and how are they used in the context of the third problem?
-Critical points are points on a function where the derivative is either zero or undefined. In the context of the third problem, the instructor finds the critical points by setting the first derivative equal to zero and then uses these points to determine the intervals where the function is increasing or decreasing.
How does the instructor determine the intervals of concavity for the function in problem four?
-The instructor finds the second derivative of the function and then determines where it is positive (concave up) and where it is negative (concave down). By testing values around the inflection points (where the second derivative is zero), the instructor establishes the intervals of concavity.
What is the second derivative test, and how is it applied in problem five?
-The second derivative test is a method used to determine whether a critical point is a local maximum, local minimum, or neither by analyzing the sign of the second derivative at that point. In problem five, the instructor finds the first and second derivatives of the given function, identifies critical points, and then applies the second derivative test to find local extrema.
In problem six, what are the steps the instructor takes to find the absolute extrema of a function on a closed interval?
-The instructor first finds any critical points within the interval by setting the first derivative to zero. Then, the function is evaluated at the critical points as well as at the endpoints of the interval. The largest and smallest values among these evaluations are identified as the absolute maximum and minimum, respectively.
What is a related rates problem, and how does the instructor approach solving problem seven?
-A related rates problem involves finding the rate at which one quantity changes with respect to another, given the rates of change of related quantities. In problem seven, the instructor uses the chain rule and implicit differentiation to find the rate at which the top of a ladder is moving down a wall when the base of the ladder is moving away from the wall at a given rate.
In the final problem, how does the instructor use calculus to find the dimensions for the largest possible rectangular outdoor storage facility given a fixed amount of fencing?
-The instructor sets up an optimization problem where the area of the rectangle (length times width) is maximized subject to the constraint that the total fencing available equals the perimeter of the rectangle. By taking the derivative of the area with respect to width, setting it to zero, and solving for width, the instructor finds the dimensions that maximize the area.
What tool does the instructor recommend for visualizing and solving calculus problems?
-The instructor recommends using desmos.com, an online graphing calculator, to visualize and better understand the calculus problems.
Outlines
📚 Calculus Midterm Exam Review
The video is a comprehensive review for a Calculus midterm exam, focusing on business and social sciences applications. It emphasizes the importance of attempting problems before watching the solutions and covers various calculus topics, including derivatives, implicit differentiation, and intervals of increase/decrease.
🔍 Simplifying Functions and Finding Derivatives
The instructor simplifies the function f(x) = x + 1/x^2 to 1/x + 1/x^2 before finding the first and second derivatives using the power rule. The process involves breaking down the fraction and canceling terms, resulting in a cleaner form for derivative calculations.
🧐 Implicit Differentiation Application
The video demonstrates the use of implicit differentiation to find the derivative of given equations. It covers four different equations, showing how to apply the product and chain rules where necessary, and solve for dy/dx in each case.
📈 Determining Intervals of Increase and Decrease
The instructor explains how to find intervals where a function is increasing or decreasing by taking the first derivative, setting it to zero to find critical points, and testing values in intervals around these points to determine the sign of the derivative.
📉 Analyzing Function Behavior with Discontinuities
The video discusses the behavior of a function with a discontinuity at x=4. It shows that the function is decreasing almost everywhere except at the point of discontinuity, emphasizing the importance of testing values before and after the discontinuity.
🤔 Conicave Up/Down and Inflection Points
The content focuses on determining whether a function is concave up or down by analyzing the second derivative. It explains the concept of inflection points and how to find them by setting the second derivative to zero and testing intervals around these points.
🏔️ Second Derivative Test for Local Extrema
The video script details the second derivative test to find local maxima and minima of a function. It involves finding the first and second derivatives, setting the first to zero to find critical points, and using the second derivative to determine if these points are maxima, minima, or inconclusive.
🔍 Related Rates Problem
The video addresses a related rates problem involving a ladder leaning against a wall. It demonstrates how to find the rate at which the top of the ladder is sliding down the wall when the base is moving away from the wall at a given rate.
🛒 Maximizing Area with Limited Resources
The final topic is an optimization problem where the goal is to find the dimensions of a rectangular storage facility that maximize the area using a limited amount of fencing. The solution involves setting up an equation based on the perimeter constraint and using calculus to find the maximum area.
Mindmap
Keywords
💡Derivative
💡Second Derivative Test
💡Implicit Differentiation
💡Critical Points
💡Concave Up/Down
💡Product Rule
💡Chain Rule
💡Related Rates
💡Optimization
💡Absolute Extrema
💡Polynomial Functions
Highlights
The importance of attempting problems before watching solutions to enhance learning.
Simplification of the function f(x) = x + 1/x^2 to 1/x + 1/x^2 for easier derivative calculation.
Use of the derivative power rule to find the first and second derivatives of a function.
Implicit differentiation technique applied to equations involving y^2 - 3x^2 + 8 = 0.
Derivative chain rule and product rule utilized to find dy/dx for equations in the form x^2y - 3x^2 - 4 = 0.
Solving for dy/dx in the context of e^y = x^2 + y^2 using the chain rule.
Second derivative test employed to determine local extrema for the function f(x) = 4 - x^6 + 6x^4.
Analysis of the function's intervals of increase and decrease based on the sign of the first derivative.
Identification of critical points and discontinuities in the function f(x) = 4/(x - 4).
Determination of concavity and inflection points for the function f(x) = x^4 - 2x^2 using the second derivative.
Application of the second derivative test to find local extrema for the function f(x) = 4 - x^6 + 6x^4, revealing a mistake in critical point calculation.
Finding absolute extrema for a quadratic function f(x) = -x^2 + 6x + 1 on a closed interval [2, 7].
Use of related rates to find the rate of change of the top of a ladder sliding down a wall as the base moves away from the wall.
Optimization problem to find the dimensions of a rectangular storage facility with the largest area using 200 feet of fencing.
The process of differentiating the area function with respect to width to find the maximum area for the storage facility.
Verification of the maximum area by comparing different width and length combinations and their respective areas.
Recommendation to use graphing calculators, such as Desmos, for visual understanding of mathematical problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: